Table of contents
アルヴェーン波 (Alfvén waves)
直感的導出
横波
磁気流体には磁気張力\(B^2/(4\pi)\)が働きます。張力\(T\)が働く線密度\(\rho\)のゴム紐では、横波が位相速度\(v = \sqrt{T/\rho}\)で伝播することからの類推により、磁気流体中を磁場に沿って位相速度
\[v_A = \frac{B}{\sqrt{4\pi \rho}} \tag{1}\]で伝播する横浪が存在すると考えられます。この速度をAlfvén速度と呼びます。具体的に宇宙物理で用いられる値を使うと
\[v_A = 2.8 \times 10^5 \left( \frac{B}{1\mu \mathrm{G}}\right) \left( \frac{n}{1 \mathrm{cm}^{-3}}\right) \ [\mathrm{cm/s}] \tag{2}\]のようになります。銀河団プラズマの典型的な値から、銀河団プラズマでは\(v_A \sim 3 \mathrm{km/s}\)となります。
縦波
同様に、磁気流体中には磁気圧\(P_m = B^2 / (8\pi)\)も働きます。磁気圧により復元力が生まれ、音波のような縦波が発生することも考えられます。ただし断熱流体の条件\(P/\rho^\gamma = \mathrm{const}\)の\(\gamma\)は、今の場合には磁束保存より
\[\frac{B}{\rho} = \mathrm{const} \ \Longrightarrow \ \frac{P_m}{\rho^2} = \mathrm{const} \tag{3}\]のようになるため、磁気圧しか働かないような流体は\(\gamma=2\)と見なすことができます。このことから、この波動の位相速度は
\[\sqrt{\frac{2P_m}{\rho}} = \frac{B}{\sqrt{4\pi \rho}} \tag{4}\]となり、やはりAlfvén速度に一致します。以上の議論から、磁気流体中で磁場を起源として伝播する波には横波と縦波の2つが存在することがわかります。それらの波のイメージを下図に示します。
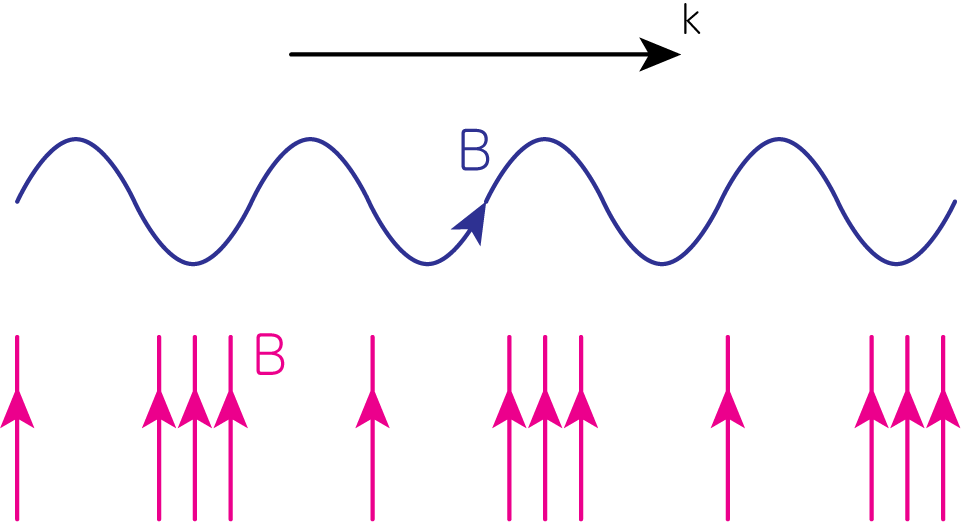
数学的導出
以上の直感的な導出での議論から、磁場により出現する波動には2種類が存在することがわかります。しかし元々、磁気張力と磁気圧による力はLorentz力\(\mathbf{j} \times \mathbf{B}\)から生まれたものです。よってこれらの波は磁場に対して沿った方向・垂直な方向だけでなく、斜め方向にも伝播しうることがわかります。よって、以下ではこの波を数学的に導出しましょう。音波を導く途中で現れた(20)式において、\(P_0 = g = \Omega = 0\)、すなわち圧力が無視できるほど影響が小さく、重力も回転もないような系で考えると
\[\begin{aligned} \omega^2 \mathbf{v}_1 &= \frac{1}{4\pi \rho_0} [\mathbf{k} \times \{ \mathbf{k} \times (\mathbf{v}_1 \times \mathbf{B}_0)\}] \underbrace{=}_{\hat{\mathbf{B}}_0 = \mathbf{B}_0/B_0} [\mathbf{k} \times \{ \mathbf{k} \times (\mathbf{v}_1 \times \hat{\mathbf{B}}_0 )\}] \times \hat{\mathbf{B}}_0 \mathbf{v}_A^2 \\ &= [(\mathbf{k} \cdot \hat{\mathbf{B}}_0) \{ (\mathbf{k} \cdot \hat{\mathbf{B}}_0) \mathbf{v}_1 - (\mathbf{v}_1 \cdot \hat{\mathbf{B}}_0) \mathbf{k} \} - (\mathbf{k} \cdot \mathbf{v}_1) \{(\mathbf{k} \cdot \hat{\mathbf{B}}_0) \hat{\mathbf{B}}_0 - \mathbf{k}\}] v_A^2 \end{aligned}\]よって
\[\frac{\omega^2}{v_A^2} \mathbf{v}_1 = (\mathbf{k} \cdot \hat{\mathbf{B}}_0)^2 \mathbf{v}_1 + \{ (\mathbf{k} \cdot \mathbf{v}_1) - (\mathbf{k} \cdot \hat{\mathbf{B}}_0) (\mathbf{v}_1 \cdot \hat{\mathbf{B}}_0)\} \mathbf{k} - (\mathbf{k} \cdot \mathbf{v}_1) (\mathbf{k} \cdot \hat{\mathbf{B}}_0) \hat{\mathbf{B}}_0\]ここで\(\hat{\mathbf{k}} = \mathbf{k}/k\)として、\(\hat{\mathbf{k}}\)と\(\hat{\mathbf{B}}_0\)の成す角を\(\theta_B\)とすると
\[\frac{\omega^2}{v_A^2} \mathbf{v}_1 = k^2 \cos^2 \theta_B \mathbf{v}_1 + \{(\mathbf{k} \cdot \mathbf{v}_1) - k \cos \theta_B (\mathbf{v}_1 \cdot \hat{\mathbf{B}}_0)\} \mathbf{k} - (\mathbf{k} \cdot \mathbf{v}_1) k \cos \theta_B \hat{\mathbf{B}}_0 \tag{5}\]となります。(5)式の両辺を\(\hat{\mathbf{B}}_0\)との内積を取ると
\[\begin{align} &\frac{\omega^2}{v_A^2} \mathbf{v}_1 \cdot \hat{\mathbf{B}}_0 = k^2 \cos^2 \theta_B (\mathbf{v}_1 \cdot \hat{\mathbf{B}}_0) + \{ (\mathbf{k} \cdot \mathbf{v}_1) - k \cos \theta_B (\mathbf{v}_1 \cdot \hat{\mathbf{B}}_0)\} - (\mathbf{k} \cdot \mathbf{v}_1) k \cos \theta_B = 0 \notag \\ &\Longrightarrow \ \mathbf{v}_1 \cdot \hat{\mathbf{B}}_0 = 0 \tag{6} \end{align}\]のようになります。よって(圧力が無視できる場合)流体の速度ベクトルの摂動量は、必ず背景磁場\(\mathbf{B}_0\)に対して垂直とわかります。これはLorentz力\(\mathbf{j} \times \mathbf{B}\)が流体に与える力が磁場に常に垂直であることから当然の結果とわかります。また基礎方程式\(\nabla \cdot \mathbf{B}_1 = \mathbf{k} \cdot \mathbf{B}_1 = 0\)が常に成り立つため、磁場の摂動は必ず波の進行方向に対して垂直であることもわかります。
ただしこの議論は線形解析の場合に限られます。非線形の場合にはより複雑な議論が必要です。
(5)式の両辺を\(\mathbf{k}\)との内積をとったものと(6)式より
\[\begin{align} &\frac{\omega^2}{v_A^2} \mathbf{k} \cdot \mathbf{v}_1 = k^2 \cos^2 \theta_B \mathbf{k} \cdot \mathbf{v}_1 + k^2 \{(\mathbf{k} \cdot \mathbf{v}_1) - k \cos \theta_B ]\underbrace{(\mathbf{v}_1 \cdot \hat{\mathbf{B}}_0)}_{(6)}\} - (\mathbf{k} \cdot \mathbf{v}_1) k^2 \cos^2 \theta_B \notag \\ &\Longrightarrow \ (\omega^2 - k^2 v_A^2 ) (\mathbf{k} \cdot \mathbf{v}_1) = 0 \tag{7} \end{align}\]シア・アルヴェーン波
(7)式のかいの一つとして\(\mathbf{k} \cdot \mathbf{v}_1 = 0\)(すなわち\(\mathbf{k} \cdot \mathbf{v}_1 = 0\)から非圧縮)があります。すると(5)式より
\[\frac{\omega^2}{v_A^2} \mathbf{v}_1 = k^2 \cos^2 \theta_B \mathbf{v}_1 \ \Longrightarrow \ v_p = \frac{\omega}{k} = v_A \cos \theta_B \tag{8}\]よって背景磁場に沿った方向\(\theta_B=0\)で位相速度は最大の\(v_A\)となりますが、背景磁場に垂直な方向\(\theta_B = \pi/2\)には波は進行しません。ここまで特に磁場の方向について触れてきませんでしたが、ここで背景磁場の方向\(\hat{\mathbf{B}}_0\)を\(z\)軸に取ると、\(k_z = k \cos \theta_B\)より
\[\mathbf{v}_g = \frac{\partial \omega}{\partial \mathbf{k}} = v_A \mathbf{e}_z \tag{9}\]となり、背景磁場の方向にしかエネルギーを運ばないことがわかります。
ここまでは\(\mathbf{k} \cdot \mathbf{v}_1 = 0\)となる解を考えてきましたが、ここでさらに\(\rho_0, P_0 = \mathrm{const}\)を仮定しましょう。すなわち波動が伝播することによる密度・圧力の変化はないものと考えます。すると線形化された誘導方程式(14)式より
となります。ここからこの波動の伝播において\(\mathbf{v}_1 \parallel \mathbf{B}_1\)となることがわかります。さらに(6)式より
\[\mathbf{B}_0 \cdot \mathbf{B}_1 = 0 \ \Longrightarrow \ \mathbf{B}_0 \perp \mathbf{B}_1 , \quad \mathbf{B}_0 \perp \mathbf{v}_1 \tag{11}\]これより、摂動として伝播していく摂動磁場は\(\mathbf{B}_1\)は背景磁場\(\mathbf{B}_0\)と垂直であることもわかります。
唐突ですが、摂動電流\(\mathbf{j}_1\)によるLorentz力について考えましょう。
右辺第1項が磁気張力による項、第2項が磁気圧勾配による項を表します。ただし(11)式より第2項は0となるので、shear Alfvén波の復元力は磁気張力のみであるとわかります。
またこの波動における磁場のエネルギーと運動エネルギーとの比を考えてみると
となることから、shear Alfvén波は磁場のエネルギーと運動エネルギーの等分配を内包していることがわかります。宇宙物理においては、例えば星間ガスでは磁場・宇宙線(非熱的粒子)・乱流・ガスの熱エネルギーの4つのエネルギーがエネルギー等分配の状態にあるとされています。
圧縮アルヴェーン波
(7)式のもう一つの解は
\[\omega = k v_A \tag{13}\]です。これをcompressional Alfvén波と呼びます。こちらは位相速度・群速度ともに\(v_A\)で、等方的に伝播していくことがわかります。(5)式から、\(\mathbf{v}_1\)は\(\hat{\mathbf{B}}_0, \mathbf{k}\)の張る平面上に存在します。また(6)式より\(\mathbf{v}_1 \perp \hat{\mathbf{B}}_0\)であることもわかります。さらに線形化された誘導方程式(14)式より
\[-i \omega \mathbf{B}_1 = i\mathbf{k} \times (\mathbf{v}_1 \times \mathbf{B}_0) = i (\mathbf{k} \cdot \mathbf{B}_0) \mathbf{v}_1 - i (\mathbf{k} \cdot \mathbf{v}_1) \mathbf{B}_0\]から\(\mathbf{B}_1\)は\(\mathbf{v}_1, \mathbf{B}_0\)の張る平面上にありますが、磁場の発散を表す(15)式より
\[\nabla \cdot \mathbf{B}_1 = \mathbf{k} \cdot \mathbf{B}_1 = 0\]から\(\mathbf{k} \perp \mathbf{B}_1\)であることもわかります。ここでLorentz力について考えましょう。\(\mathbf{k}\)と\(\mathbf{B}_0\)の成す角度が\(\theta_B\)であったことを思い出すと
\[\mathbf{j}_1 \times \mathbf{B}_0 = i \frac{4\pi}{c} (kB_0 \cos \theta_B \mathbf{B}_1 + B_0 B_1 \sin \theta_B \mathbf{k}) = i \frac{4\pi}{c} k B_0 B_1 (\cos \theta_B \hat{\mathbf{B}}_1 + \sin \theta_B \hat{\mathbf{k}})\]のようになり、これは\(\mathbf{v}_1\)の方向に一致します。そのため、compressional Alfvén波は磁気張力と磁気圧の両方が復元力となって伝播します。\(\theta_B = \pi/2\)(\(\mathbf{B}_0\)に対して垂直方向)のとき\(\mathbf{v}_1 \parallel \mathbf{k}\)となり、これは縦波を表します。\(\theta_B =0\)(\(\mathbf{B}_0\)と同じ方向)のとき、これはshere Alfvén波に一致し、compressionalと呼びながらも横波となります。
背景磁場と摂動ベクトルの方向の関係を下図に示します。下左図がshear Alfvén波、下右図がcompressional Alfvén波です。
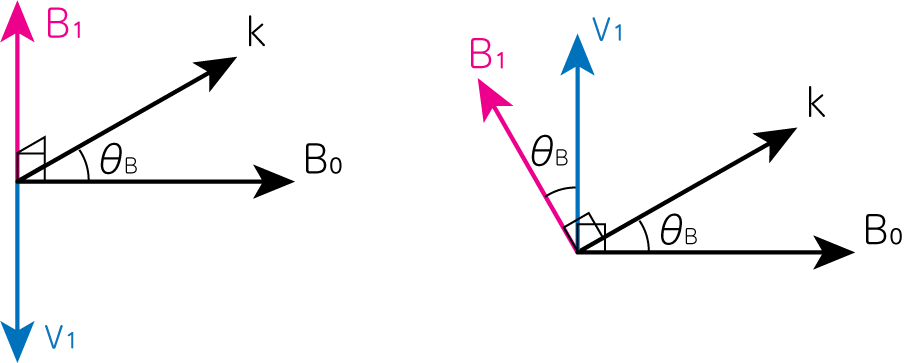
フリードリックスダイアグラム
ここまでで磁気流体中を磁場を介して伝播する波を2つ考えてきましたが、背景磁場\(\mathbf{B}_0\)に対する波動の伝播方向によって位相速度が変化することがわかりました。これを1つの図としてまとめることができます。これをFriedricks diagramと呼びます。下左図が位相速度、下右図が群速度を表します。
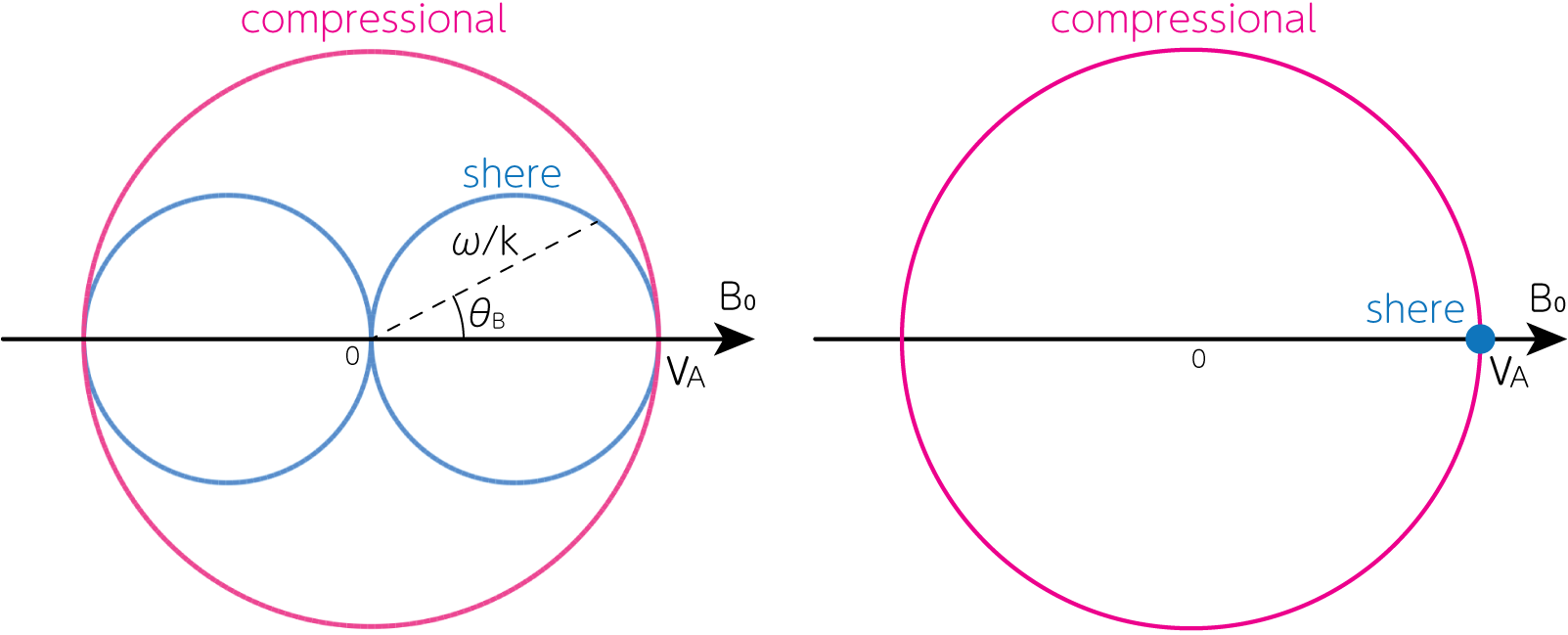
参考文献
[1] Priest, “Solar Magnetohydrodynamics”
[2] Spitzer, “Physics of Fully Ionized Gases”
[3] Spitzer, “Physical Processes in the Interstellar Medium”
[4] 観山正見, 野本憲一, 二間瀬敏史, “天体物理学の基礎 II”