Table of contents
パパロイゾウ・プリングル不安定性 (Papaloizou-Pringle Instability: PPI)
ここでは、コンパクト天体などの周囲に存在するトーラスの安定性について調べた、Papaloizou & Pringle (1984)について勉強したことをメモします。
導出
基礎方程式の線形化
まずは基礎方程式を考えましょう。 質量保存の式は
\[\frac{\partial \rho}{\partial t} + \nabla \cdot (\rho \mathbf{v}) = 0 \tag{1}\]です。 続いて運動方程式は
\[\frac{\partial \mathbf{v}}{\partial t} + (\mathbf{v} \cdot \nabla) \mathbf{v} = - \frac{1}{\rho} \nabla P - \nabla \psi \tag{2}\]と書けます。 ここで\(\psi\)は、ブラックホールなどの中心天体が作る重力ポテンシャルで
\[\psi = - \frac{GM}{\sqrt{R^2 + z^2}} \tag{3}\]のように書かれます。 最後に、状態方程式としてポリトロープを仮定しましょう。
\[P = A \rho^\gamma \quad \left( \gamma \equiv 1 + \frac{1}{n} \right) \tag{4}\]以上が基礎方程式となります。
平衡状態: ブラックホール周りのトーラス
次に平衡状態として、ブラックホール周りのトーラス (ドーナツ状の構造) を考えましょう。 その\(z=0\)面内での運動や密度・圧力の変化について考察していきます。
このとき、平衡状態の流体の運動\(\mathbf{v}_0\)は、\(z=0\)面内で半径\(R\)の場所を円運動しているとします。
\[\mathbf{v}_0 (R) = R \Omega (R) \mathbf{e}_\varphi \tag{5}\]また平衡状態の密度と圧力をそれぞれ\(\rho_0 (R, z), P_0(R, z)\)としましょう。 トーラスは時間に依存せず、定常的にその形を保っているため、この平衡状態は以下の式を満たします。
\[\frac{\partial \rho_0}{\partial t} = 0, \quad \frac{\partial P_0}{\partial t} = 0, \quad \frac{\partial \mathbf{v}_0}{\partial t} = \mathbf{0} \tag{6}\](6)式と(1), (2), (4)より
\[\nabla \cdot (\rho_0 \mathbf{v}_0) = 0 \tag{7}\] \[(\mathbf{v}_0 \cdot \nabla ) \mathbf{v}_0 = - \frac{1}{\rho_0} \nabla P_0 - \nabla \psi \tag{8}\] \[P_0 = A \rho_0^\gamma \tag{9}\]も満たすことがわかります。
方程式の線形化
次に、この系に摂動が加わった場合を考えていきましょう。 摂動量には1の添え字をつけて表現することにします。 すなわち
\[\rho = \rho_0 + \rho_1, \quad P = P_0 + P_1, \quad \mathbf{v} = \mathbf{v}_0 + \mathbf{v}_1 \tag{10}\]のように状態が変化したとします。 このとき\(\rho_1, P_1, \vert \mathbf{v}_1 \vert\)は微小量であることから、1の添え字がついた量に対しては1次の項だけを残すことにし、2次以上の高次の項は無視します。 (1)式より
\[\begin{align} \frac{\partial}{\partial t} (\rho_0 + \rho_1) + \nabla \cdot \{(\rho_0 + \rho_1) (\mathbf{v}_0 + \mathbf{v}_1)\} &\underbrace{=}_{(6)} \frac{\partial \rho_1}{\partial t} + \nabla \cdot (\rho_0 \mathbf{v}_0 + \rho_1 \mathbf{v}_0 + \rho_0 \mathbf{v}_1) \notag \\ &\underbrace{=}_{(7)} \frac{\partial \rho_1}{\partial t} + \nabla \cdot (\rho_1 \mathbf{v}_0 + \rho_0 \mathbf{v}_1) = 0 \tag{11} \end{align}\]です。 続いて、(4)式より
\[\begin{align} P_0 + P_1 &= A (\rho_0 + \rho_1)^\gamma = A \rho_0^\gamma \left( 1 + \frac{\rho_1}{\rho_0}\right)^\gamma \approx A \rho_0^\gamma \left( 1 + \frac{\gamma \rho_1}{\rho_0}\right) = A \rho_0^\gamma + \gamma A \rho_0^\gamma \frac{\rho_1}{\rho_0} \notag \\ &\underbrace{=}_{(9)} P_0 + \gamma P_0 \frac{\rho_1}{\rho_0} \ \Longrightarrow \ P_1 = \gamma P_0 \frac{\rho_1}{\rho_0} \tag{12} \end{align}\]となります。 最後に、(2)式について考えましょう。
\[\begin{aligned} (左辺) &= \frac{\partial}{\partial t} (\mathbf{v}_0 + \mathbf{v}_1) + \{(\mathbf{v}_0 + \mathbf{v}_1) \cdot \nabla\} (\mathbf{v}_0 + \mathbf{v}_1) \notag \\ &\underbrace{=}_{(6)} \frac{\partial \mathbf{v}_1}{\partial t} + (\mathbf{v}_0 \cdot \nabla) \mathbf{v}_0 + (\mathbf{v}_1 \cdot \nabla ) \mathbf{v}_0 + (\mathbf{v}_0 \cdot \nabla) \mathbf{v}_1 \end{aligned}\] \[\begin{aligned} (右辺) &= - \frac{1}{\rho_0 + \rho_1} \nabla (P_0 + P_1) - \nabla \psi = - \frac{1}{\rho_0} \frac{1}{1 + \rho_1 / \rho_0} \nabla (P_0 + P_1) - \nabla \psi \notag \\ &\approx - \frac{1}{\rho_0} \left( 1 - \frac{\rho_1}{\rho_0}\right) \nabla (P_0 + P_1) - \nabla \psi = - \frac{1}{\rho_0} \nabla P_0 + \frac{\rho_1}{\rho_0^2} \nabla P_0 - \frac{1}{\rho_0} \nabla P_1 - \nabla \psi \end{aligned}\]これらと(8)式より
\[\frac{\partial \mathbf{v}_1}{\partial t} + (\mathbf{v}_1 \cdot \nabla) \mathbf{v}_0 + (\mathbf{v}_0 \cdot \nabla) \mathbf{v}_1 = \frac{\rho_1}{\rho_0^2} \nabla P_0 - \frac{1}{\rho_0} \nabla P_1 \tag{13}\]のようになります。 さらに
\[\frac{\rho_1}{\rho_0^2} \nabla P_0 \underbrace{=}_{(9)} \frac{\rho_1}{\rho_0^2} A \gamma \rho_0^{\gamma -1} \nabla \rho_0 = \frac{\gamma \rho_1 P_0}{\rho_0^3} \nabla \rho_0 \underbrace{=}_{(12)} \frac{P_1}{\rho_0^2} \nabla \rho_0 \tag{14}\]のように変形できることから
\[\frac{\partial \mathbf{v}_1}{\partial t} + (\mathbf{v}_1 \cdot \nabla) \mathbf{v}_0 + (\mathbf{v}_0 \cdot \nabla) \mathbf{v}_1 = \frac{P_1}{\rho_0^2} \nabla \rho_0 - \frac{1}{\rho_0} \nabla P_1 = - \nabla \left(\frac{P_1}{\rho_0} \right) = - \nabla \left(\frac{P_1}{\rho} \right) \tag{15}\]のようになります。 ここで微小量の2次の項は無視することから、最後の等号では\(\frac{P_1}{\rho_0} = \frac{P_1}{\rho_0 + \rho_1} = \frac{P_1}{\rho}\)のようにしました。
フーリエモード
\(\varphi, t\)に対する摂動フーリエモードのみを考えることにしましょう。 すなわち\(\rho_1, p_1, v_{R 1}, v_{\varphi 1}, v_z \propto \exp \{i (m \varphi + \sigma t)\}\)の形で式を変形していきます。 すると(11)式より
\[\begin{align} &i\sigma \rho_1 + \mathbf{v}_0 \cdot (\nabla \rho_1) + \rho_1 \underbrace{(\nabla \cdot \mathbf{v}_0)}_{=0} + \nabla \cdot (\rho_0 \mathbf{v}_1) = i \sigma \rho_1 + im \Omega \rho_1 + \nabla \cdot (\rho_0 \mathbf{v}_1) = 0 \notag \\ &\Longrightarrow \ i (\sigma + m \Omega) \rho_1 = - \nabla \cdot (\rho \mathbf{v}_1) \tag{16} \end{align}\]ここでも、\(\rho_0 \mathbf{v}_1 = (\rho_0 + \rho_1) \mathbf{v}_1 = \rho \mathbf{v}_1\)のようにしました。 同様に(15)式の\(R, \varphi, z\)成分それぞれについても書き下してみましょう。 まずは\(R\)成分からです。
\[\frac{\partial v_{1R}}{\partial t} + \left( - \frac{v_{1\varphi} v_{0\varphi}}{R} \right) + \left( \frac{v_{0\varphi}}{R} \frac{\partial v_{1R}}{\partial \varphi} - \frac{v_{0\varphi} v_{1\varphi}}{R} \right) = i (\sigma + m \Omega) v_{1R} - 2\Omega v_{1\varphi} = - \frac{\partial}{\partial R} \left( \frac{P_1}{\rho} \right)\]さらに右辺は
\[\frac{\partial}{\partial R} \left\{ (\sigma + m \Omega) \frac{P_1}{\rho (\sigma + m\Omega)} \right\} = (\sigma + m\Omega) \frac{\partial W}{\partial R} + m W \frac{\partial \Omega}{\partial R} = (\sigma + m\Omega) \frac{\partial W}{\partial R} - \frac{3m \Omega W}{2R}\]のように変形されます。 ここで
\[W \equiv \frac{P_1}{\rho (\sigma + m \Omega)} \tag{17}\]と定義し、さらに
\[\frac{\partial \Omega}{\partial R} = \frac{\partial}{\partial R} \sqrt{\frac{GM}{R^3}} = - \frac{3}{2} \sqrt{\frac{GM}{R^5}} = - \frac{3\Omega}{2R}\]のようにしました。 以上から\(R\)成分の式は
\[v_{1R} + \frac{2 i \Omega}{\sigma + m\Omega } v_{1\varphi} = i \frac{\partial W}{\partial R} + \frac{3m \Omega W}{2iR (\sigma + m\Omega)} \tag{18}\]次に\(\varphi\)成分です。
\[\begin{align} \frac{\partial v_{1\varphi}}{\partial t} + \left( v_{1R} \frac{\partial v_{0\varphi}}{\partial R}\right) + \left( \frac{v_{0\varphi}}{R} \frac{\partial v_{1\varphi}}{\partial \varphi} + \frac{v_{0\varphi} v_{1R}}{R}\right) &= i\sigma v_{1\varphi} + v_{1R} \frac{d}{dR} (R \Omega) + im \Omega v_{1\varphi} + \Omega v_{1R} \notag \\ &= i(\sigma + m \Omega) v_{1\varphi} + v_{1R} \left( R \frac{d\Omega}{dR} + 2\Omega \right) \notag \\ &= i(\sigma + m \Omega) v_{1\varphi} + \frac{v_{1R}}{R} \left( R^2 \frac{d\Omega}{dR} + 2R \Omega \right) \notag \\ &= i(\sigma + m \Omega) v_{1\varphi} + \frac{v_{1R}}{R} \frac{d}{dR} (R^2 \Omega) = - \frac{im}{R} \frac{P_1}{\rho} \tag{19} \end{align}\]ここで、エピサイクリック振動数
\[\kappa^2 = \frac{2\Omega}{R} \frac{d}{dR} (R^2 \Omega) \tag{20}\]を用いると
\[v_{1\varphi} + \frac{\kappa^2}{2i \Omega (\sigma + m\Omega) }v_{1R} = - \frac{mW}{R} \tag{21}\]を得ます。 最後に\(z\)成分です。
\[\frac{\partial v_{1z}}{\partial t} + \frac{v_{0\varphi}}{R} \frac{\partial v_{1z}}{\partial \varphi} = i (\sigma + m \Omega) v_{1z} = - \frac{\partial}{\partial z} \left( \frac{P_1}{\rho} \right) \ \Longrightarrow \ v_{1z} = i \frac{\partial W}{\partial z}\tag{21}\](18), (21)式より
\[v_{1\varphi} = \frac{\bar{\sigma}^2}{\bar{\sigma}^2 - \kappa^2} \left( - \frac{\kappa^2}{2\bar{\sigma} \Omega} \frac{\partial W}{\partial R} + \frac{3m\kappa^2 W}{4\bar{\sigma}^2 R} - \frac{mW}{R}\right) \tag{22}\]これを(18)に代入すれば
\[\begin{align} v_{1R} &= - \frac{2i\Omega}{\sigma + m \Omega} \frac{\bar{\sigma}^2}{\bar{\sigma}^2 - \kappa^2} \left( - \frac{\kappa^2}{2\bar{\sigma} \Omega} \frac{\partial W}{\partial R} + \frac{3m\kappa^2 W}{4\bar{\sigma}^2 R} - \frac{mW}{R}\right) + i \frac{\partial W}{\partial R} + \frac{3m\Omega W}{2iR\bar{\sigma}} \notag \\ &= i \frac{\bar{\sigma}^2}{\bar{\sigma}^2 - \kappa^2} \left( \frac{\partial W}{\partial R} + \frac{m\Omega W}{2 \bar{\sigma} R}\right) \tag{23} \end{align}\]を得ます。 (21), (22), (23)式を(16)式に入れて整理することで、\(W\)に関する微分方程式を得ることができます。
\[\begin{align} i \bar{\sigma} \rho_1 &= - \frac{1}{R} \frac{\partial}{\partial R} (\rho R v_{1R}) - \frac{1}{R} \frac{\partial}{\partial \varphi} (\rho v_{1\varphi}) - \frac{\partial}{\partial z} (\rho v_{1z}) \notag \\ &= - \frac{1}{R} \frac{\partial}{\partial R} \left\{ i \rho R \frac{\bar{\sigma}^2}{\bar{\sigma}^2 - \kappa^2} \left( \frac{\partial W}{\partial R} + \frac{m\Omega W}{2 \bar{\sigma} R}\right)\right\} \notag \\ & \qquad \qquad - \frac{1}{R} \frac{\partial}{\partial \varphi} \left\{ \rho \frac{\bar{\sigma}^2}{\bar{\sigma}^2 - \kappa^2} \left( - \frac{\kappa^2}{2 \bar{\sigma} \Omega} \frac{\partial W}{\partial R} + \frac{3m\kappa^2 W}{4 \bar{\sigma}^2 R} - \frac{mW}{R} \right)\right\} - \frac{\partial}{\partial z} \left( i \rho \frac{\partial W}{\partial z} \right) \notag \end{align}\]第二項において、\(W = \frac{P_1}{\rho \bar{\sigma}}\)は1次の微小量なので、\(\rho\)は\(\rho_0\)として扱うことができます。 今は軸対称なトーラス構造を考えているため、\(\frac{\partial \rho}{\partial \varphi}= 0\)とできます。 そして\(D \equiv \bar{\sigma}^2 - \kappa^2\)を定義し、さらに\(\frac{\partial W}{\partial \varphi} = i m W\)であることを用いると
\[\begin{align} &i \bar{\sigma} \rho_1 = - \frac{i}{R} \frac{\partial}{\partial R} \left\{ \frac{\rho \bar{\sigma}^2 R}{D} \left( \frac{\partial W}{\partial R} + \frac{m\Omega W}{2 \bar{\sigma} R}\right) \right\} - \frac{im \rho \bar{\sigma}^2}{RD} \left( - \frac{\kappa^2}{2 \bar{\sigma} \Omega} \frac{\partial W}{\partial R} + \frac{3m\kappa^2 W}{4 \bar{\sigma}^2 R} - \frac{mW}{R} \right) - i \frac{\partial}{\partial z} \left( \rho \frac{\partial W}{\partial z} \right) \notag \\ &\underbrace{\Longrightarrow}_{(12)} \ \frac{1}{R} \frac{\partial}{\partial R} \left\{ \frac{\rho \bar{\sigma}^2 R}{D} \left( \frac{\partial W}{\partial R} + \frac{m\Omega W}{2 \bar{\sigma} R}\right) \right\} + \frac{m \rho \bar{\sigma}^2}{RD} \left( - \frac{\kappa^2}{2 \bar{\sigma} \Omega} \frac{\partial W}{\partial R} + \frac{3m\kappa^2 W}{4 \bar{\sigma}^2 R} - \frac{mW}{R} \right) \notag \\ & \qquad \qquad \qquad + \frac{\partial}{\partial z} \left( \rho \frac{\partial W}{\partial z} \right) + \frac{\bar{\sigma}^2 \rho^2 W}{\gamma P} = 0 \tag{24} \end{align}\]のようになります。 ケプラー運動においては
\[\kappa^2 = \frac{2\Omega}{R} \frac{d}{dR} \left( R^2 \Omega \right) = \frac{2\Omega}{R} \left( 2R \Omega + R^2\frac{d\Omega}{dR} \right) = \frac{2\Omega}{R} \left( 2R \Omega - R^2 \frac{3\Omega}{2R}\right) = \Omega^2\]より、最終的に
\[\begin{align} &\frac{1}{R} \frac{\partial}{\partial R} \left\{ \frac{\rho \bar{\sigma}^2 R}{D} \left( \frac{\partial W}{\partial R} + \frac{m\kappa^2 W}{2 \bar{\sigma} R \Omega}\right) \right\} + \frac{m \rho \bar{\sigma}^2}{RD} \left( - \frac{\kappa^2}{2 \bar{\sigma} \Omega} \frac{\partial W}{\partial R} + \frac{3m\kappa^2 W}{4 \bar{\sigma}^2 R} - \frac{mW}{R} \right) \notag \\ & \qquad \qquad \qquad + \frac{\partial}{\partial z} \left( \rho \frac{\partial W}{\partial z} \right) + \frac{\bar{\sigma}^2 \rho^2 W}{\gamma P} = 0 \tag{25} \end{align}\]を得ます。 一般のトーラス構造の場合を考えるのは困難を極めるため、以下ではより簡単な場合について見ていきましょう。
一定の比角運動量トーラスの安定性
比角運動量\(h = R^2 \Omega\)が一定の場合を考えましょう。 このとき\(\kappa = 0\)、そして\(D = \bar{\sigma}^2\)となることから、(25)式は以下のようになります。
\[\frac{1}{R} \frac{\partial}{\partial R} \left( \rho R \frac{\partial W}{\partial R} \right) - \frac{m^2}{R^2} \rho W + \frac{\partial}{\partial z} \left( \rho \frac{\partial W}{\partial z}\right) + \frac{\bar{\sigma}^2 \rho^2 W}{\gamma P} = 0 \tag{26}\]この式をさらに整理するために、\(\sigma_c \equiv \sigma + m \Omega_c\)を定義しておきましょう。 ここで\(\Omega_c\)はある一定の角速度です(この値については後述。) すると
\[\bar{\sigma}^2 = (\sigma + m \Omega + m \Omega_c - m \Omega_c)^2 = (\sigma_c + m \Omega - m \Omega_c)^2 = \sigma_c^2 + 2m(\Omega - \Omega_c) \sigma_c + m^2 (\Omega - \Omega_c)^2 \tag{27}\]のように変形されるため
\[\begin{align} &\frac{1}{R} \frac{\partial}{\partial R} \left( \rho R \frac{\partial W}{\partial R} \right) - \frac{m^2}{R^2} \rho W + \frac{\partial}{\partial z} \left( \rho \frac{\partial W}{\partial z}\right) + \frac{\rho^2 W}{\gamma P} \{ \sigma_c^2 + 2m(\Omega - \Omega_c) \sigma_c + m^2 (\Omega - \Omega_c)^2 \} \notag \\ &= \sigma_c^2 \frac{\rho^2}{\gamma P} W + 2m (\Omega - \Omega_c) \sigma_c \frac{\rho^2}{\gamma P} W + \frac{1}{R} \frac{\partial}{\partial R} \left( \rho R \frac{\partial W}{\partial R} \right) - \frac{m^2}{R^2} \rho W + \frac{\partial}{\partial z} \left( \rho \frac{\partial W}{\partial z}\right) + \frac{m^2 (\Omega - \Omega_c)^2 \rho^2}{\gamma P} W \notag \\ &= \sigma_c^2 A W + \sigma_c B W + CW = 0 \tag{28} \end{align}\]となります。 ここで
\[A = \frac{\rho^2}{\gamma P}, \quad B = \frac{2m(\Omega - \Omega_c) \rho^2}{\gamma P} \tag{29}\]であり、\(C\)は楕円作用素と呼ばれるもので
\[CW = \frac{1}{R} \frac{\partial}{\partial R} \left( \rho R \frac{\partial W}{\partial R}\right) + \frac{\partial}{\partial z} \left( \rho \frac{\partial W}{\partial z}\right) + \rho m^2 W \left\{ \frac{\rho (\Omega - \Omega_c)^2}{\gamma P} - \frac{1}{R^2}\right\} \tag{30}\]のように定義されます。 次に、(28)式の両辺に\(RW^\ast\)をかけ、それを\((R, z)\)平面内のトーラスの存在する領域で積分します。 ただし、\(\ast\)は複素共役を意味します。 すると
\[(第一項) = \iint \sigma_c^2 A \vert W \vert^2 A R dR dz = \sigma_c^2 \bar{A} \tag{31}\] \[(第二項) = \iint \sigma_c B \vert W \vert^2 R dR dz = \sigma_c \bar{B} \tag{32}\]第三項において、トーラスの内縁と外縁では\(\rho(R_\mathrm{in}, z) = \rho(R_\mathrm{out}, z) = 0\)であることを用いると
\[\begin{align} \int_{R_\mathrm{in}}^{R_\mathrm{out}} \frac{1}{R} \frac{\partial}{\partial R} \left( \rho R \frac{\partial W}{\partial R}\right) W^\ast R dR &= \left[ \rho R \frac{\partial W}{\partial R} W^\ast \right]_{R_\mathrm{in}}^{R_\mathrm{out}} - \int_{R_\mathrm{in}}^{R_\mathrm{out}} \rho R \frac{\partial W}{\partial R} \frac{\partial W^\ast}{\partial R} dR \notag \\ &= - \int_{R_\mathrm{in}}^{R_\mathrm{out}} \rho R \left\vert \frac{\partial W}{\partial R} \right\vert^2 dR \tag{33} \end{align}\]さらに\(\rho(R, z_\mathrm{bottom}) = \rho(R, z_\mathrm{top}) = 0\)であることを用いれば
\[\begin{align} \int_{z_\mathrm{bottom}}^{z_\mathrm{top}} \frac{\partial}{\partial z} \left( \rho \frac{\partial W}{\partial z}\right) W^\ast dz &= \left[ \rho \frac{\partial W}{\partial z} W^\ast \right]_{z_\mathrm{bottom}}^{z_\mathrm{top}} - \int_{z_\mathrm{bottom}}^{z_\mathrm{top}} \rho \frac{\partial W}{\partial z} \frac{\partial W^\ast}{\partial z} dz \notag \\ &= - \int_{z_\mathrm{bottom}}^{z_\mathrm{top}} \rho \left\vert \frac{\partial W}{\partial z} \right\vert^2 dz \tag{34} \end{align}\]より
\[\begin{align} (第三項) &= \iint CW R W^\ast dR dz \notag \\ &= - \iint \rho \left[ \left\vert \frac{\partial W}{\partial R}\right\vert^2 + \left\vert \frac{\partial W}{\partial z}\right\vert^2 + m^2 \vert W \vert^2 \left\{ \frac{1}{R^2} - \frac{\rho (\Omega - \Omega_c)^2}{\gamma P}\right\} \right] R dR dz \notag \\ &= - \bar{C} \tag{35} \end{align}\]のように整理されます。 以上から(28)式は
\[\sigma_c^2 \bar{A} + \sigma_c \bar{B} - \bar{C} = 0 \tag{36}\]のようになります。 この式は\(\sigma_c\)の2次関数なので、解は
\[\sigma_c = \frac{-\bar{B} \pm \sqrt{\bar{B}^2 + 4 \bar{A} \bar{C}}}{2\bar{A}} \tag{37}\]となります。 ここで\(\bar{A}, \bar{B}, \bar{C}\)は全て実数です。 \(\sigma_c\)が実数であれば、\(\sigma\)も実数となります。 これはフーリエモードの形\(\exp \{i(m \varphi + \sigma t)\}\)から、全ての\(m\)に対して安定な振動となることがわかります。 逆に\(\sigma_c\)が複素数となれば、\(\sigma\)も虚数を持つことになり、これは不安定な波動となります。 このことから(37)式で\(\bar{C}\)が負になることが、不安定性が発生する条件となります。 (35)式を見ると、マイナス符号を持つのは\(- \frac{\rho (\Omega - \Omega_c)^2}{\gamma P}\)の部分のみです。 もし\(\gamma \rightarrow \infty\)の非圧縮極限ならば、(\(P/\rho\)が有限という仮定のもとで)全ての\(m\)に対して安定となることがわかります。 このことから、この系の不安定性は、音速が有限の値となることから発生すると考えることができます。
一般固有値問題
ここでは一般固有値問題として、(26)式の固有値が複素数になるかどうかを調べてみましょう。 この議論をするためには、\(W\)に対する境界条件が必要となります。 トーラスの境界部分では\(\rho = 0\)であることを考えてきましたが、解析的に求めるためには\(W\)は正則でなければなりません。 そこで、境界部分では\(\rho\)は小さい値ながら、有限であるとします。
以下のような線形な演算子を定義しましょう。
すると(26)式は
\[L(W) = - \frac{(\sigma + m\Omega)^2 \rho^2 W}{\gamma P} \tag{39}\]となります。 この方程式に\(L\)の逆変換を作用させることで、積分方程式を得ることができます。 (39)式を\(L(W) = S\)のように書くことにすると
\[W = L^{-1} (S) = \iint G(R, z, R', z') S(R', z') dR' dz' \tag{40}\]を得ます。 ここで\(G(R, z, R', z')\)は適切に選択されたグリーン関数です。 以上から、この固有値問題は
\[W + L^{-1} \left( \frac{(\sigma + m\Omega)^2 \rho^2 W}{\gamma P}\right) = 0 \tag{41}\]のようになります。
この方程式を解く議論は私には難しすぎました...とりあえずこの説明はここまでですorz
クライン・ゴルドン方程式とのアナロジー
後のために、(39)式を次のように書き直しておきましょう。
\[L(W) = - \frac{\alpha^2 m^2 (\nu + \Omega)^2}{\gamma P} \rho^2 W \tag{42}\]ここで\(\nu \equiv \sigma /m\)です。 そして\(\alpha\)は適当なパラメータで、\(\alpha = \pm 1\)の場合には(39)式に一致します。
この方程式において不安定となる\(\nu\)の固有値は、実はクライン・ゴルドン方程式からの類推から予想することができます。 電荷\(e\)と質量\(m\)を持つ粒子の波動関数を\(\psi\)、そして静電ポテンシャルを\(\phi\)とすると
のように書かれます。 ここで\(E\)はエネルギー固有値です。 もし粒子が有限領域に閉じ込められているとき(すなわち\(\psi\)が境界でゼロとなるとき)、固有値は離散化されます。 そしてもし\(\phi\)が小さければ、固有値\(E\)は正負どちらもとる実数となります。 \(\phi\)の大きさが\(2mc^2\)を超えると、正の最低エネルギー固有値と負の最高エネルギー固有値が合体し、固有値の複素数ペアを生み出します。 これはクラインのパラドックスと呼ばれ、のちにこれは粒子・反粒子の生成を意味します。 クライン・ゴルドン方程式において、\(E = -\alpha \nu, \phi = \alpha \Omega /e\)のように定義し、さらに楕円作用素を
\[L' (\psi) \equiv -m^2 c^4 \psi + \hbar^2 c^2 \nabla^2 \psi \tag{44}\]としましょう。 すると(43)式は
\[L'(\psi) = -\alpha^2 (\nu + \Omega)^2 \psi \tag{45}\]のようになります。 これは(39)式に類似しています。 楕円作用素\(L'\)は\(L\)と少しだけ異なりますが、同じ数学的特徴を持ちます。 このことからも、(26)式からある\(m\)に対して不安定な解 (\(\sigma\)が複素数となる解)の存在が示唆されます。
解析的に解ける例
ここでは解析的に解ける、さらに簡単な例を見ていきましょう。
薄い円筒
ここでは、平衡状態にある薄い円筒について見ていきましょう。 ガスは\(R_0 \leq R \leq R_0 + a\)の領域のみに存在するとします。 このとき\(a \ll R_0\)とします。 この場合、密度と圧力は定数として扱ってよく、また\(z\)方向については考える必要がありません。 すると(26)式は
\[\frac{1}{R} \frac{d}{dR} \left( R \frac{dW}{dR} \right) - \frac{m^2 W}{R^2} = - \frac{\bar{\sigma}^2 \rho W}{\gamma P} \tag{46}\]のようになります。 ここで、\(x = R - R_0 \ (x \ll R_0)\)のような変数を導入しましょう。 また\(\frac{m^2}{R_0^2} \ll \frac{1}{a^2}\)のように、\(m\)がそこまで大きくないモードについてのみ考えることにしましょう。 すると第一項は
\[\frac{1}{R} \frac{d}{dR} \left( R \frac{dW}{dR} \right) = \frac{1}{x + R_0} \frac{d}{dx} \left\{ (x + R_0) \frac{d W}{dx}\right\} \approx \frac{d}{dx} \left( \frac{x}{R_0} \frac{dW}{dx} \right) + \frac{d^2 W}{dx^2} \underbrace{\approx}_{x/R_0 \ll 1} \frac{d^2 W}{dx^2} \tag{47}\]のように整理されるので
\[\frac{d^2 W}{dx^2} = - \frac{\bar{\sigma}^2 \rho W}{\gamma P} \tag{48}\]となります。 \(\bar{\sigma} (R) = \sigma + m \Omega(R)\)を\(R = R_0\)の周りでテイラー展開し、整理しましょう。
\[\bar{\sigma}(R)^2 = (\sigma + m\Omega)^2 = \left( \sigma + m \Omega(R_0) + m \left. \frac{d\Omega}{dR} \right\vert_{R=R_0} x \right)^2 = \mu^2 (\lambda + x)^2 \tag{49}\]ここで\(\mu \equiv m \left. \frac{d\Omega}{dR} \right\vert_{R=R_0}, \lambda \equiv \frac{\sigma + m \Omega(R_0)}{\mu}\)です。 以上より
\[\frac{d^2 W}{dx^2} = - k^2 (\lambda + x)^2 W \qquad \left( k \equiv \frac{\rho \mu^2}{\gamma P}\right) \tag{50}\]を得ます。 (50)式の解は、ベッセル関数を用いて以下のように書くことができます。
\[W = C_1 F_1 (x) + C_2 F_2 (x) \tag{51}\]ここで\(C_1, C_2\)は任意の定数、そして
\[F_1(x) = \{(x+\lambda)^2\}^{1/4} J_{1/4} \left(\frac{k(x+\lambda)^2}{2}\right), \quad F_2(x) = \{(x+\lambda)^2\}^{1/4} J_{-1/4} \left(\frac{k(x+\lambda)^2}{2}\right) \tag{52}\]です。
この解が不安定かどうかを調べるために、\(\lambda = \lambda_\mathrm{R} + i\delta\)のように、\(\lambda\)が小さな虚部\(\delta\)を持つ場合の解の振る舞いを考えてみましょう。 ここで\(\lambda_\mathrm{R}<0, \vert \lambda_\mathrm{R} \vert < a\)であるとします。 すなわち、\(\lambda_\mathrm{R}+x\)は、\(0 < x < a\)のある点でその符号を変えることになります。 \(\lambda\)に対する固有値方程式における境界条件は、次のように書くことができます。
これを計算するために、\(F_1, F_2\)の微分を計算しましょう。
\[F_1'(x) = \frac{1}{2} (x+\lambda)^{-1/2} J_{1/4} \left(\frac{k(x+\lambda)^2}{2}\right) + (x+\lambda)^{1/2} \frac{dJ_{1/4}}{dz} \frac{dz}{dx} \tag{54}\]途中、\(z = \frac{k(x+\lambda)^2}{2}\)としました。 さらに\(k \gg 1\)の場合を考えましょう。 ベッセル関数の漸近形より
\[J_{\nu} (z) \approx \sqrt{\frac{2}{\pi z}} \cos \left( z - \frac{2\nu + 1}{4} \pi \right) \ \Longrightarrow \ \frac{dJ_\nu}{dz} \approx - \sqrt{\frac{2}{\pi z}}\sin \left( z - \frac{2\nu + 1}{4} \pi \right) \tag{55}\]です。 (54)式において、第二項には\(\frac{dz}{dx} = k(x+\lambda)\)があることから、\(k \gg 1\)ではこの項が優勢となり、第一項は無視することができます。 すると、\(\nu = 1/4\)を代入して
\[F_1'(x) \approx (x+\lambda)^{1/2} \left( \frac{4k}{\pi}\right)^{1/2} \sin \left( \frac{k(x+\lambda)^2}{2} - \frac{3\pi}{8}\right) \tag{56}\]のようになります。 ここから
\[F_1'(0) \approx - (-\lambda)^{1/2} \sqrt{\frac{4k}{\pi}} \sin \left( \frac{k\lambda^2}{2} - \frac{3\pi}{8}\right) \tag{57}\] \[F_1' (a) \approx - (\lambda + a)^{1/2} \sqrt{\frac{4k}{\pi}} \sin \left( \frac{k(\lambda + a)^2}{2} - \frac{3\pi}{8}\right) \tag{58}\]を得ます。 同様に
\[F_2' (0) \approx (-\lambda)^{1/2} \sqrt{\frac{4k}{\pi}} \sin \left( \frac{k\lambda^2}{2} - \frac{\pi}{8}\right) \tag{59}\] \[F_2' (a) \approx - (\lambda + a)^{1/2} \sqrt{\frac{4k}{\pi}} \sin \left( \frac{k(\lambda+a)^2}{2} - \frac{\pi}{8}\right) \tag{60}\]を得ることができます。 (57), (59)式の\((-\lambda)^{1/2}\)では、正の実数の場合のみを取ります。 これらを(53)式に代入すると
\[\sqrt{2} \sin \left[ \frac{k}{2} \left\{ \lambda^2 + (\lambda + a)^2 \right\}\right] = \cos \left[ \frac{k}{2} \left\{ \lambda^2 - (\lambda + a)^2 \right\}\right] \tag{61}\]となります。 (61)式の解を、\(\lambda = -\frac{1}{2} a + i \delta\)の形で見つけることにしましょう。 すると
\[\cosh (ka \delta) = \sqrt{2} \sin \left\{ k \left( \frac{1}{4} a^2 - \delta^2\right) \right\} \tag{62}\]この式は、ある\(k\)に対して\(\delta\)が正の値の解を持つことを意味します。 \(ka^2 \gg 1\)かつ\(\delta \ll a\)の場合を考え、\(ka\delta \sim \mathcal{O}(1)\)程度であると考えると
\[\frac{1}{\sqrt{2}} \cosh (ka\delta) = C_0 < 1\]であるとわかります。 ここから
\[\frac{1}{4}ka^2 \left( 1 - \frac{4\delta^2}{a^2}\right) = \sin^{-1} C_0 + 2N\pi \qquad (N \gg 1)\]のようになります。 この不安定性の典型的な成長率は、\(ka\delta \sim 1\)から求めることができます。
\[- \mathrm{Im}(\sigma) = - \delta \mu \simeq \frac{\vert \mu \vert}{k a} = \sqrt{\frac{\gamma P}{\rho a^2}} \tag{63}\]以上から、不安定性の成長の時間スケールは音波横断時間スケールであり、不安定性が力学的タイムスケールで起こることがわかります。
薄い等温リング
続いて、中心天体の重力場の影響下にある等温ガスリングについて考えてみましょう。 このリングは\(R=R_0\)を中心に存在しているとします。 また等温であることから、一定の音速\(C_s\)を用いてその状態方程式は\(P = \rho C_s^2\)で与えられるとします。 先程の薄い円筒の場合と同様に、\(x = R - R_0\)のような変数を考え、さらに\(x/ R_0, z/R_0 \ll 1\)とします。 リング中のガスは運動を行っておらず、平衡状態にあるとすると、その運動方程式は重力・遠心力・圧力勾配の力の釣り合いから
\[- \frac{1}{\rho} \frac{\partial P}{\partial R} - \frac{\partial \psi}{\partial R} + \Omega^2 R = 0\]です。 これを\(R\)で積分することで
\[C_s^2 \ln \rho + \psi + \frac{h^2}{2R^2} = C \ (定数) \tag{64}\]となります。 ここで\(h\)はガスの比角運動量です。 重力ポテンシャル(3)式を、\(R=R_0, z=0\)の周りでテイラー展開すると
\[\psi = - \frac{GM}{R_0} \left( 1 - \frac{x}{R_0} + \frac{2x^2 - z^2}{2R_0^2} + \cdots \right) \tag{65}\]を得ます。 同様に
\[\frac{h^2}{2R^2} = \frac{h^2}{2R_0^2} \left( 1 - \frac{2x}{R_0} + \frac{3x^2}{R_0^2} + \cdots \right) \tag{66}\]です。 これらを代入し、(64)式の\(x, z\)の2次のオーダーまでを計算しましょう。
\[C_s^2 \ln \rho + \left( \frac{GM}{R_0^2} - \frac{h^2}{R_0^3}\right) x - \frac{GM}{2R_0^3} (2x^2 - z^2) + \frac{3h^2 x^2}{2 R_0^4} = D \tag{67}\]ここで\(D\)は\(C\)とは異なる定数です。 \(h^2 = GM R_0\)であることを用いると、密度が
\[\rho = \rho_0 \exp\left\{ - \frac{GM}{2R_0^3 C_s^2} (x^2 + z^2)\right\} \tag{68}\]の ように求まります。 ここで\(\rho_0\)は\(x = z= 0\)、すなわち\((R, z )= (R_0, 0)\)に位置するリング最深部での密度です。 温度が下がる(\(C_s\)が小さい)と、密度の集中度がより大きくなることがわかります。
このリングの密度分布が判明したところで、次はこの系の安定性を議論していきましょう。 そのために、(26)式から振り返っていきましょう。 (26)式において\(x/R_0 \ll 1\)かつ\(\gamma = 1\)の場合を考えると
のようになります。 ここで先程の薄い円筒の場合と同じ表現を用いました。 この場合
\[k^2 = \frac{4m^2 \Omega^2 (R_0)}{C_s^2 R_0^2} = \frac{4m^2}{b^2 R_0^2}, \quad \lambda = - \frac{(\sigma + m \Omega (R_0)) R_0}{2m\Omega(R_0)}, \quad b^2 = \frac{C_s^2 R_0^3}{GM}\tag{70}\]です。 (68)式を用いて\(\rho\)を消去しましょう。 すると
\[\frac{\partial^2 W}{\partial x^2} - \frac{x}{b^2} \frac{\partial W}{\partial x} + \frac{\partial^2 W}{\partial z^2} - \frac{z}{b^2} \frac{\partial W}{\partial z} - \frac{m^2 W}{R_0^2} = - k^2 (x+\lambda)^2 W \tag{71}\]のような\(W\)の微分方程式を得ることができます。 この方程式の解を
\[W = G_1(x) G_2(z) \tag{72}\]のように変数分離した形で求めることにします。 すると
\[\frac{d^2 G_1}{dx^2} - \frac{x}{b^2} \frac{dG_1}{dx} - \frac{m^2 G_1}{R_0^2} - \Lambda G_1 + k^2 (\lambda + x)^2 G_1 = 0 \tag{73}\] \[\frac{d^2 G_2}{dz^2} - \frac{z}{b^2} \frac{dG_2}{dz} + \Lambda G_2 = 0 \tag{74}\]となります。 ここで\(\Lambda\)は、分離をしたときの定数です。 (74)式の\(G_2(z/b)\)はエルミート多項式の微分方程式を満たします。 その解から\(\Lambda = n_1 / b^2 \ (n_1 = 0, 1, 2, \dots)\)のみに限られることがわかります。
(73)式を解くために、次のような変換を行いましょう。
ここで\(a_1, a_2\)はそれぞれ
\[a_1^2 + \frac{a_1}{b^2} + k^2 = 0, \quad a_2 = - \frac{2\lambda k^2}{2a_1 + b^{-2}} \tag{76}\]を満たします。 そして\(G_3\)は、以下の微分方程式を満たします。
\[\frac{d^2 G_3}{dx^2} - \frac{dG_3}{dx} \{(2a_1 + b^{-2}) x + 2a_2\} + G_3 \left( k^2 \lambda^2 - \frac{m^2}{R_0^2} - \frac{n_1}{b^2} + a_2^2 - a_1\right) = 0 \tag{77}\]これは再びエルミート方程式になっていることがわかります。 よって\(G_3\)は
\[y = (2a_1 + b^{-2})^{1/2} \left( x + \frac{2a_2}{2a_1 + b^{-2}}\right) \tag{78}\]を変数とするエルミート多項式関数として求まります。 そしてこの解は
\[k^2 \lambda^2 - \frac{m^2}{R_0^2} - \frac{n_1}{b^2} + a_2^2 - a_1 = (2a_1 + b^{-2}) n_2 \quad (n_2 = 0, 1, 2, \dots) \tag{79}\]により制限されます。 各\(n_1, n_2\)に対し、(76), (79)式により固有値\(\lambda\)を決定することができます。 (76)式を\(a_1\)について解きましょう。
\[a_1 = - \frac{1}{2b^2} \pm \sqrt{\frac{1}{4n^4} - k^2} \tag{80}\]簡単のため、マイナス符号の解のみを考えることにすると\(\lambda\)は
\[k^2 \lambda^2 = (1-4k^2 b^4) \left\{ \frac{n_1 - \frac{1}{2}}{b^2} + \frac{m^2}{R_0^2} + \left( n_2 + \frac{1}{2}\right) \sqrt{\frac{1}{b^4} - 4k^2}\right\} \tag{81}\]のようになります。 不安定なモードを調べるには、\(\lambda\)が複素数となるような解が存在するかどうかを調べれば良いでしょう。 そのためには、(81)式の右辺が負でなければなりません。 そのための必要条件は\(n_1 = 0\)とわかります。 よって、不安定モードは\(z\)方向には依存しません。 そして\(k^2 = \frac{4m^2}{b^2 R_0^2}\)であることを思い出すと、不安定となる条件が
\[2m^2 \epsilon^2 + (2n_2 + 1) \sqrt{1-16 m^2 \epsilon^2} < 1 \tag{82}\]と求まります。 ここで\(\epsilon \equiv b / R_0 \ll 1\)です。 \(\xi = 16 m^2 \epsilon^2 = 4k^2 b^4\)のように定義すると、(82)式の条件は
\[2n_2 + 1 < \frac{1 - \frac{1}{8} \xi}{\sqrt{1-\xi}} \tag{83}\]のようになります。 もし\(\xi = 0\)、すなわち\(m=0\)ならば、この不等式は任意の\(n_2\)で満たされず、常に安定です。 (83)式の右辺は\(\xi\)の単調増加関数であるため、\(\xi\)が\(0\rightarrow 1\)のように増加すると、\(n_2\)の大きな値が不等式を満たしていくことになります。 また\(k^2\)が大きくなるほど、不安定なモードが増えていくこともわかります。 最も素早く成長する不安定性のモードは\(n_2=0\)の基本振動です。 \(\epsilon\)が十分小さく、\(\xi\)が連続関数として扱える場合、最も早い成長率は\(m \approx 0.19 R_0 / b \ (0.24 C_s / b = 0.24 \Omega (R_0))\)と求まります。 このことから、先程の薄い円筒の場合と同様に、この系でも力学的な時間スケールで不安定性が起こることがわかります。
最近の研究
磁気流体トーラスでのPPI
ここまでPPIの議論をしてきましたが、実際の降着トーラスは磁場を持つ磁気流体として記述されます。 磁気流体トーラスでのPPI不安定性を線形解析した研究が、Fu & Lai (2011)です。 トロイダル磁場が存在する場合にその不安定性を調べたところ、薄いトーラスでは、大きな磁場強度の場合には不安定性が抑制されることがわかりました。 また分厚いトーラスの場合には、十分強い磁場の場合には、逆に不安定性が発生することが判明したのです。

Fu & Lai (2011)より。横軸はアルヴェーン速度の\(\phi\)成分の大きさ、縦軸はトーラスの厚さ。
磁場強度の大きいトーラスは、通常の磁気回転不安定性に対して安定な場合でも、PPIのようなトーラス全体の不安定性を受ける可能性があることを示唆しました。
PPIによる重力波の発生
先程の薄い等温リングでの議論から、PPIでは基本振動モードが一番成長しやすいことがわかります。 すなわち軸対称なトーラスは、PPIにより一本腕の非軸対称な構造になることがわかります。 それを3次元一般相対論的流体シミュレーションにより調べたのが、Kiuchi et al. (2011)です。 また非軸対称な構造は力学的時間スケールよりも長い時間に渡って維持され、大振幅の準周期的な重力波の放射源となることを示しました。
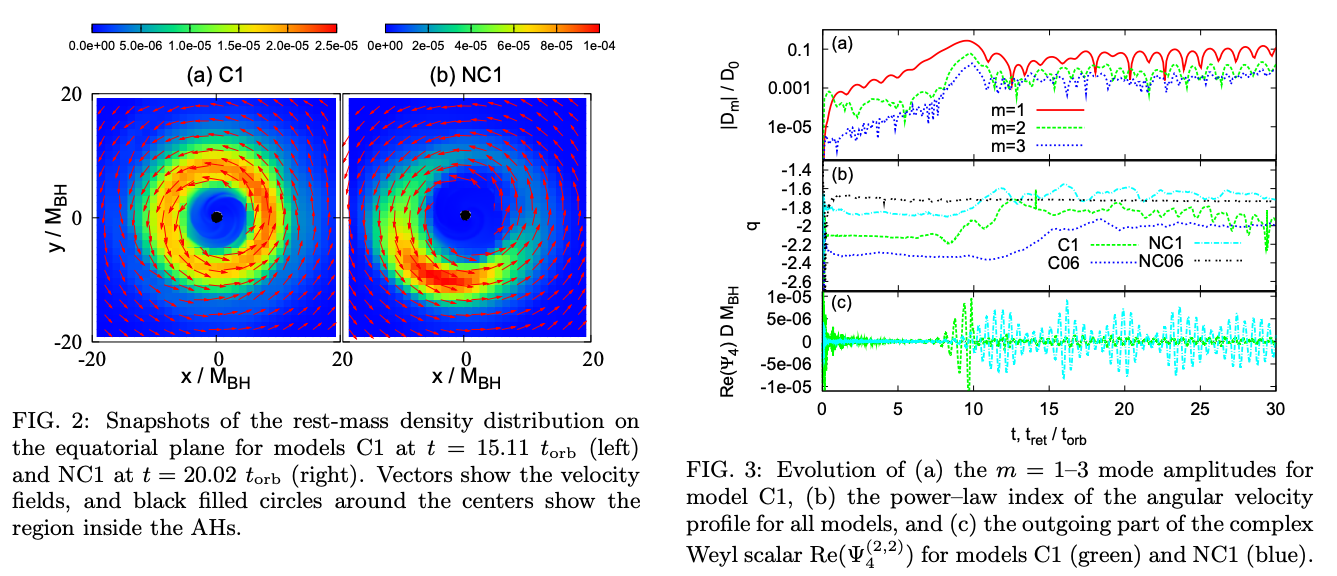
Kiuchi et al. (2011)より。左パネルはシミュレーションから得られた軸対称と非軸対称のガス分布、右パネルの一番下のグラフが重力波の波形に対応するもの。
銀河中心に存在する超大質量ブラックホール(SMBH)とその周囲に存在するトーラスが、今後の宇宙重力波検出器で観測される可能性を示したのです。
参考文献
[1] Papaloizou & Pringle, 1984, “The dynamical stability of differentially rotating discs with constant specific angular momentum”
[2] Papaloizou & Pringle, 1985, “The dynamical stability of differentially rotating discs - II”
[3] Abramowicz et al., 1987, “A New Example of the Papaloizou-Pringle Instability”
[4] Fu & Lai, 2011, “Papaloizou-Pringle instability of magnetized accretion tori”
[5] Kiuchi et al., 2011, “Gravitational Waves from the Papaloizou-Pringle Instability in Black-Hole-Torus Systems”
[6] 花輪知幸, “回転流体の安定性と回転円盤の進化”