宇宙線 (Cosmic Rays: CRs)

円形加速器では、磁場(と電場)を巧みに用いることで荷電粒子を高エネルギーまで加速することができます。宇宙にもあまねく磁場が存在し、その環境次第では高エネルギー粒子の生成現場となっているような天体があります。ここではそれらの天体がどの程度まで陽子を加速できるかを推定し、それが地球に飛来できるのかどうかを見積もってみましょう。

相対論的陽子のラーモア半径と運動エネルギー

ここでは大雑把な推定のために、ある天体が一様磁場を持っているとします。この一様磁場中を相対論的速度を持つ陽子が、一様磁場に垂直な方向に運動している場合を考えましょう(もし水平成分を持っていたとしてもその方向には等速度で運動をするだけなので、問題には特に影響しません)。すると、この相対論的陽子の円運動の半径は、ラーモア半径より

\[\begin{align} &r_L = \frac{v}{\omega_\mathrm{se}} = \frac{m_p \gamma c}{e B} v = \underbrace{\frac{m_p c}{eB}}_{\equiv \alpha^{-1}} \frac{cv}{c^2 - v^2} \ \Longrightarrow \ \alpha^2 r_L^2 = \frac{c^2 v^2}{c^2 - v^2} \notag \\ &\Longrightarrow \ (c^2 + \alpha^2 r_L^2) v^2 = \alpha^2 r_L^2 c^2 \ \Longrightarrow \ \beta^2 = \left( \frac{v}{c}\right)^2 = \frac{\alpha^2 r_L^2}{c^2 + \alpha^2 r_L^2} \tag{1} \end{align}\]

この式から、ローレンツ因子\(\gamma\)がラーモア半径\(r_L\)と

\[\gamma = \frac{1}{\sqrt{1-(v/c)^2}} = \sqrt{1 + (r_L / c)^2 \alpha^2} \tag{2}\]

のような関係にあることがわかります。相対論より、超相対論的な陽子\((\gamma \gg 1)\)の運動エネルギーは\(T = m_p \gamma c^2\)のように書けるので

\[T = m_p c^2 \sqrt{1 + (r_L / c)^2 \alpha^2} \tag{3}\]

のように表されます。ここで、途中で定義した\(\alpha\)を計算しておきましょう。

\[\begin{align} \alpha^2 &= \frac{e^2 B^2}{m_p^2 c^2} = \underbrace{\frac{e^2}{\hbar c}}_{=1/137} \frac{\overbrace{\hbar c}^{=197 \mathrm{MeV} \cdot \mathrm{fm}} c^2}{\underbrace{(m_p c^2)^2}_{(938 \mathrm{MeV})^2}} B^2 \simeq \frac{2 \times 10^{-11}}{140} \frac{9 \times 10^{20}}{10^6 \mathrm{MeV}} B^2 \simeq \frac{9}{70} \frac{10^3}{1 \mathrm{MeV}} B^2 \notag \\ &\simeq \frac{9}{70} \frac{10^3}{10^6 \times 1.6 \times 10^{-12}} B^2 \simeq \frac{9}{112} \times 10^9 \left( \frac{B}{1 \mu \mathrm{G}}\right)^2 10^{-12} \simeq 8 \times 10^{-5} \left( \frac{B}{1 \mu \mathrm{G}}\right)^2 \tag{4} \end{align}\]

低エネルギーの陽子が天体内部で加速され高エネルギーになっていくと、いずれはラーモア半径がその天体サイズを越えてしまい、天体の外に飛び出します。すると天体の磁場による軌道の曲がりを受けなくなるため、その相対論的陽子は宇宙の彼方へ飛び去ることがわかります。当然ながら、これ以上はその天体内部で加速されることはありません。よってラーモア半径が天体のサイズと一致する程度になったときを、その天体内部での加速の限界と定めましょう。以下では例として

1pc程度の大きさの超新星残骸
10kpc程度の大きさの銀河円盤

について、相対論的陽子が加速されうる最大のエネルギーを見積もります。さらに大雑把に考えるために、以下では磁場の強度を\(1 \mu \mathrm{G}\)とします。

超新星残骸の場合 (サイズ1pc)

\(r_L = 1 \mathrm{pc} \sim 3 \times 10^{18} \mathrm{cm}\)のとき

\[\begin{align} T &\sim 938 \mathrm{MeV} \times \sqrt{1 + \left(\frac{3 \times 10^{18}}{3 \times 10^{10}} \times 8 \times 10^{-5} \right)^2} \sim 938 \times \sqrt{8 \times 10^{11}} [\mathrm{MeV}] \notag \\ &\sim 9.38 \times 2\sqrt{2} \times 10 \times 10^7 [\mathrm{MeV}] \sim 8 \times 10^{5} [\mathrm{GeV}] \tag{5} \end{align}\]

およそ\(10^{6} \mathrm{GeV}\)となることがわかります。

もちろんこれは大雑把な見積もりです。実際の超新星残骸では、磁場が衝撃波面で大きく増幅されています。

銀河円盤の場合 (サイズ10kpc)

\(r_L = 10 \mathrm{kpc} \sim 3 \times 10^{22}\)のとき、(5)式と同様の計算を行うことで

\[T \sim 8 \times 10^{9} [\mathrm{GeV}] \tag{6}\]

およそ\(10^{10} \mathrm{GeV}\)となります。

宇宙線スペクトル

ここまでの大雑把な見積もりを踏まえて、実際に観測されている、地球へと飛来した宇宙線のエネルギースペクトルを見てみましょう。

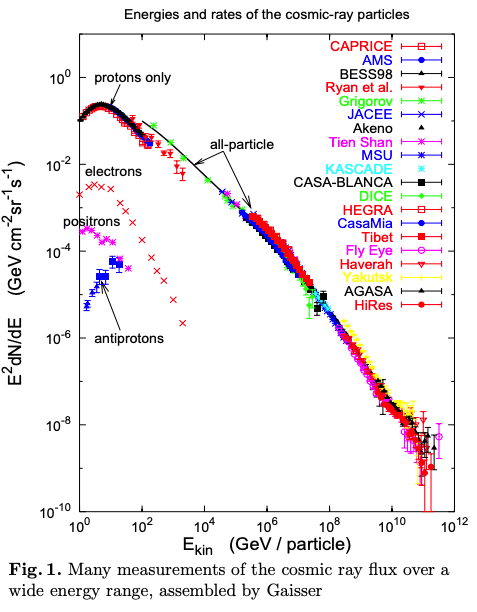
上図は縦軸が単位時間・単位立体角・単位面積・単位エネルギーあたりに飛来する宇宙線の頻度にエネルギーの2乗を掛けたもの、そして横軸は宇宙線のエネルギーです。宇宙線の飛来頻度にエネルギーの2乗をかけることで、エネルギーが増加するにつれて急激に減少するグラフを見やすくしています。上図を見ると、\(10^6\mathrm{GeV}\)あたりと\(10^{9-10}\mathrm{GeV}\)のあたりにわずかながら折れ曲がりを見ることができます。このグラフを人間の足に見立てて、前者を膝”knee”、そして後者を足首”ankle”と呼びます。先程の2つの大雑把な見積もりから、この2つの折れ曲がり部分は宇宙線の加速現場の違いを反映していると推察することができます。すなわちkneeより低エネルギー側は超新星残骸やそれより小さな天体が起源、そしてkneeより大きくankleより小さいエネルギーの宇宙線は天の川銀河起源であると言えます。それよりも高エネルギーのものはより大きなスケール、すなわち銀河系外から飛来してきているものと考えることができます。

参考文献

[1] Hillas, 2006, “Cosmic Rays: Recent Progress and some Current Questions”
[2] The IceCube Masterclass website
[3] FAST Project website