Table of contents
1次元ニューラルネットワークの万能近似定理
ニューラルネットワークには、どのような関数も近似して表現することができる万能近似定理(univearsal approximation theorem; 普遍性定理とも訳される)があります。以下ではこの証明を追っていきましょう。
以下の説明は”これならわかる機械学習”の4.2.1章部分を分かりやすくするために、自分なりに図の挿入や式変形などを行ったものです。
問題設定
簡単のため入力はスカラー\(x\)ただ一つ、そして隠れ層(入力でも出力でもない中間層)は1層とします。
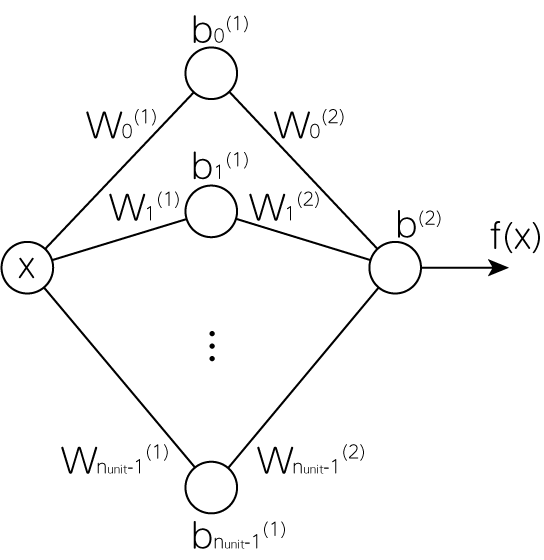
すると1層目の出力は
\[L_i^{(1)} = g(w_i^{(1)} x + b_i^{(1)}) \qquad (i \in [0, 1, \dots, n_\mathrm{unit}-1]) \tag{1}\]のようになります。ここで\(g\)はユニット部分の活性化関数です。今、問題をさらに簡単にするために活性化関数をステップ関数\(g = \sigma_\mathrm{step}\)のようにします。すると出力される値は
\[f(x) = \sum_{i=0}^{n_\mathrm{unit}-1} w_i^{(2)} L_i^{(1)} + b^{(2)} = \sum_{i=0}^{n_\mathrm{unit}-1} w_i^{(2)} \sigma_\mathrm{step} \left( w_{i}^{(1)} x + b_i^{(1)} \right)+ b^{(2)} \tag{2}\]となります。
各層で何が起こるのか
いきなり出力された(2)式から何が起こっているのかを判断するのは難しいため、1層目と2層目で何が起こっているのかを\(n_\mathrm{unit}=1\)の場合に見てみましょう。このとき1層目から出力されるのは、(1)式より
\[L_0^{(1)} (x) = \sigma_\mathrm{step} (w_0^{(1)} x + b_0^{(1)})\]です。ここで\(w_0^{(1)} \neq 0\)とすると
\[L_0^{(1)} (x) = \sigma_\mathrm{step} (w_0^{(1)} (x- \tilde{b}_0^{(1)})) \qquad (\tilde{b}_0^{(1)} \equiv - b_0^{(1)} / w_0^{(1)})\]のように変形することができます。よって\(\tilde{b}_0^{(1)}\)の値によって、ステップの場所を任意に定めることが可能です。
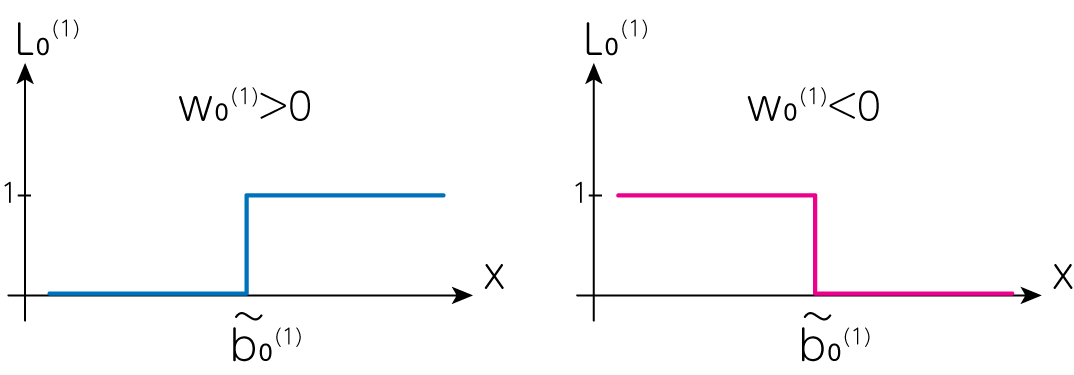
ここにさらに\(w_0^{(2)}\)をかけた
\[w_0^{(2)} \sigma_\mathrm{step} \left(w_0^{(1)}(x - \tilde{b}_0^{(1)}) \right)\]は\(w_0^{(2)}\)によってステップの高さを自由に調整できる関数であり、そしてここにバイアスを追加した
\[f(x) = w_0^{(2)} \sigma_\mathrm{step} \left(w_0^{(1)}(x - \tilde{b}_0^{(1)}) \right) + b^{(2)}\]はステップ全体の値を変えることが可能であることがわかります。
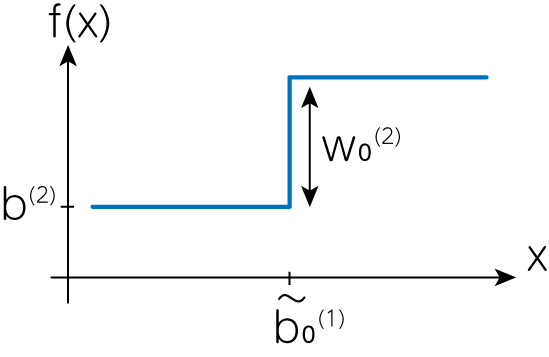
このようにして自由にステップの始まる高さやステップそれ自体の高さ、そしてステップ全体の値を設定できることから、\(n_\mathrm{unit}\)を増やすことで任意の関数を近似的に表現することができるようになるとわかります。
ユニットを増やす
例えば\(n_\mathrm{unit}=2\)としてみましょう。先程と同様に\(\tilde{b}_i^{(1)} = -b_i^{(1)} / w_i^{(1)} \ (i = 0, 1)\)とすると
\[f(x) = w_0^{(2)}\sigma_\mathrm{step} (w_0^{(1)}(x-\tilde{b}_0^{(1)})) + w_1^{(2)}\sigma_\mathrm{step} (w_1^{(1)}(x-\tilde{b}_1^{(1)})) + b^{(2)} \tag{3}\]のようになります。ここで例えば\(w_0^{(1)} = w_1^{(1)} = 1, \tilde{b}_0^{(1)} = 0.5, \tilde{b}_1^{(1)} = -0.5, w_0^{(2)} = -1, w_1^{(2)} = 1, b^{(2)} = 0\)のように定めれば
\[f(x) = \left\{ \begin{array}{cl} 1 & (-0.5 \leq x \leq 0.5) \\ 0 & (\mathrm{otherwise}) \end{array} \right.\]のような矩形関数を描くことができます。2つのユニットから矩形を1つ作ることができるので、これを増やしていけばどのような関数でも近似することができます。このような理由から1次元ニューラルネットワークは任意の連続関数を望む精度で表現することが可能です。
参考文献
[1] 富谷昭夫, “これならわかる機械学習”
[2] Michael Nielsen, “Neural Networks and Deep Learning” website, Chapter 4