白色矮星の振動

概要

白色矮星の中には、周期が\(100\sim 1000\)秒の変光を示すものがあります。それらは白色矮星のg-mode振動により、主に表面温度が変化することで起こるものです。白色矮星の自由落下時間は数秒であるため、それらの振動は動径方向モードやp-modeではありえません。単周期のものはまれで、ほとんどの場合には同時にいくつものモードの振動が存在し、ビートにより振幅が一定ではありません。振幅は0.01magから0.3magまでと、多様に存在します。

物理量の抽出

白色矮星の振動の観測から正確な周期を得ることで、白色矮星の質量・水素の層の厚さ・自転周期などの情報を引き出すことができます。また周期の時間変化が検出できれば、進化の速さを評価することも可能です。 g-mode振動に対し、動径方向の波数\(k_r\)は、特に\(k_r \gg k_h\)のとき

\[k_r \simeq \frac{N}{r\sigma} \sqrt{\ell (\ell + 1)} \tag{1}\]

のように表されます。ここで\(k_h \equiv \sqrt{\frac{\ell (\ell + 1)}{r}}\)は水平方向の波数、\(N\)はBrunt-Väisälä振動数、そして\(\sigma\)は角振動数を表します。大局的振動の振動数は、量子化条件

\[n\pi = \int_{r_1}^{r_2} k_r dr = \frac{\sqrt{\ell (\ell + 1)}}{\sigma} \int_{r_1}^{r_2} \frac{N}{r} dr \tag{2}\]

によって求まります。ここで\(n\)は整数、\(r_1, r_2\)は\(k_r\)が実数となる(伝搬可能な)層の境界の中心からの距離を表します。したがって、白色矮星の振動周期は

\[\Pi = \frac{2\pi}{\sigma} \propto \frac{n}{\sqrt{\ell (\ell + 1)}} \left( \int_{r_1}^{r_2} \frac{N}{r} dr\right)^{-1} \tag{3}\]

のように表されます。

この辺の導出もしっかり解説する予定です。しかしいつになることやら...

水素は軽く、不透明度が大きいため、比較的広がった構造を持ちます。そのため表面の水素の層の質量が大きいと、振動が伝搬可能な層の厚さ \(r_2 - r_1 (\ll r)\)が大きいため、比較的周期が短くなります。この性質から、観測される最も短い周期をモデルと比較することにより、水素層に含まれる質量を評価することができます。またBrunt-Väisälä振動数は温度が下がるとその値が減少するため、ある振動モードの周期は、白色矮星の冷却が進むに連れて長くなっていきます。それを計測することで、冷却率の観測的な評価をすることができます。期待される周期変化率は、1年で\(10^{-7} \mathrm{s}\)程度のわずかな量です。そのため、これを観測的に決定するには、何年にも渡る観測が必要となります。現在のところ得られている結果は、理論モデルの値と同程度であると知られています。
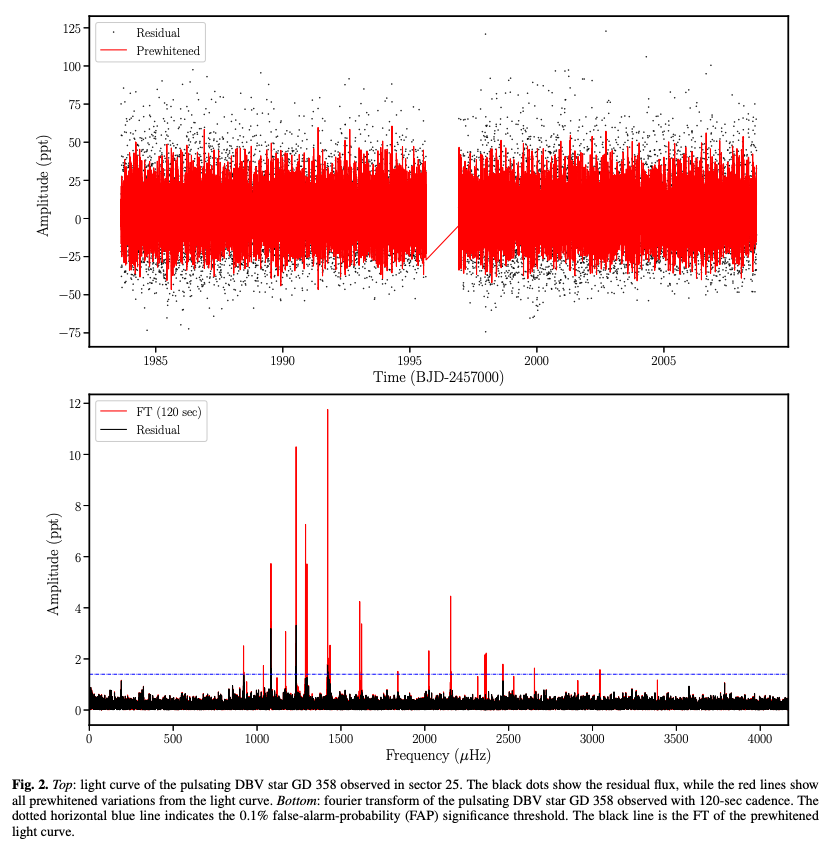
次の図の上パネルは、振動する(DB型)白色矮星の光度曲線の例です。

Corsico et al. (2022)より

このような変光は、複数の固有振動の重ね合わせ \(\sum_j A_j \exp (2\pi i \nu_j t)\)として表されます。この光度曲線をフーリエ変換することにより、下パネルのようなパワースペクトルが得られ、振動数を知ることができます。

参考文献

[1] Corsico et al., 2022, “Pulsating hydrogen-deficient white dwarfs and pre-white dwarfs observed with TESS III. Asteroseismology of the DBV star GD 358”
[2] Shapiro & Teukolsky, “Black Holes, White Dwarfs, and Neutron Stars”

白色矮星の振動

概要

分類

物理量の抽出

参考文献