Table of contents
分散量度 (Dispersion Measure: DM)
冷たい等方プラズマ中の電磁波による情報伝搬について議論していきましょう。 情報伝搬の速度は群速度で与えられます。 すると冷たい等方プラズマ中の電磁波の伝播ページの(19)式より
\[v_g = \frac{d\omega}{dk} = c \sqrt{1 - \frac{\omega_\mathrm{pe}^2}{\omega^2}} \underbrace{\simeq}_{\omega \gg \omega_\mathrm{pe}} c \left( 1- \frac{\omega_\mathrm{pe}^2}{2 \omega^2}\right) < c \tag{1}\]を得ます。 ここから、天体から放射されたパルスが観測者に到達するまでにかかる時間\(t_p\)を計算しましょう。 天体から観測者までの距離を\(d\)とすると
\[t_p = \int_0^d \frac{ds}{v_p} \simeq \frac{d}{c} + \frac{1}{2c\omega^2} \int_0^d \omega_\mathrm{pe}^2 ds = \frac{d}{c} + \frac{2\pi e^2}{m_e c\omega^2} \int_0^d n_e ds \tag{2}\]のように計算されます。 第一項の\(d/c\)は距離\(d\)を光の速度で伝搬した場合にかかる時間です。 第二項は電子密度\(n_e\)のプラズマが存在することによるパルスの到達の遅れを表します。 そこで、この部分を以下のように表記しましょう。
\[\begin{align} \Delta t_p &= \frac{2\pi e^2}{m_e c \omega^2} \mathrm{DM} = \frac{e^2}{\hbar c} \hbar c \frac{c}{m_e c^2} \frac{1}{(2\pi \nu)^2} \mathrm{DM} \notag \\ &\simeq \frac{200 \mathrm{MeV \cdot fm}}{140} \frac{3 \times 10^{10} \mathrm{cm \cdot s^{-1}}}{0.5 \mathrm{MeV}} \frac{10^{-18}}{6} \left(\frac{\nu}{1 \mathrm{GHz}} \right)^{-2} 3 \times 10^{18} \left( \frac{\mathrm{DM}}{1 \mathrm{pc \cdot cm}^{-3}} \right) \notag \\ &\simeq 4 \left( \frac{\nu}{1 \mathrm{GHz}}\right)^{-2} \left( \frac{\mathrm{DM}}{1 \mathrm{pc \cdot cm^{-3}}} \right) \ [\mathrm{ms}] \quad \left( \mathrm{DM} \equiv \int_0^d n_e ds \right) \tag{3} \end{align}\]このDMは、宇宙物理研究では通常\(\mathrm{pc} \ \mathrm{cm}^{-3}\)という単位で表され、これを分散量度 (Dispersion Measure: DM)と呼びます。 これは\(1 \mathrm{cm}^{-3}\)のプラズマ中をDM pcだけ伝搬してきたことを表す量です。 プラズマの電子数密度が既知である場合、時間の遅れを測定することでDMを求め、天体までの距離\(d\)の測定を行うことができます。 (24)式から、時間の遅れは電磁波の周波数の2乗に逆比例しています。 これを利用し、複数の周波数でパルス放射の到達時間を測定すれば、DMを測定することが可能です。
最近、高速電波バースト(Fast Radio Burst: FRB)が多数報告されるようになりました。 この現象の発生原因は未だ解明されていませんが、この電波パルスを用いてDMと距離を測定することで、FRBが発生した周囲のプラズマの情報を得る研究がされています。 FRBが生まれる天体はどのような姿をしているのか、その発生源を探るためにも、その周囲の環境について精査することは非常に重要な研究と位置付けられています。
実際にFRBまでの距離を求めてみよう
以下では観測結果をもとに、実際にFRBまでの距離を推定してみましょう。 下図はFRBの最初の発見報告である、Lorimer et al., 2007から抜粋した電波観測結果です。
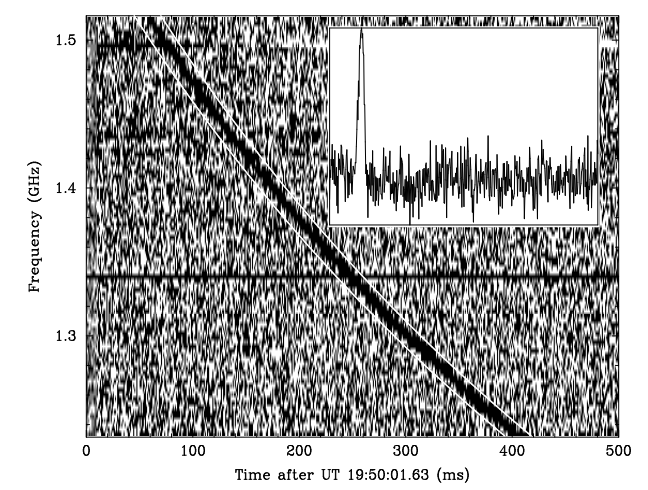
この図は縦軸に周波数(GHz)、横軸にパルスの到達時間をとったものです。 図の黒い線がシグナルであり、例えば1.4GHzのチャンネルではある時刻から約200ms後にシグナルを受け取ったことを表しています。 (3)式から高周波ほど到達時間が早いため、この図は上に行くほど周波数が大きいこともわかります。
この図を見ると、1.4GHzでは約200msで到達しているのに対し、約1.3GHzでは300msで到達しているとわかります。 このことから、この二つの周波数での時間差はは100msです。 二つの周波数\(\nu_1, \nu_2\)のパルスの到達の時間差をさらに\(\Delta\)とすれば
から、DMを求めることができます。よって
\[100 = 4 \left\{ \left( \frac{1}{1.3} \right)^2 - \left( \frac{1}{1.4} \right)^2 \right\} \mathrm{DM} \ \Longrightarrow \ \mathrm{DM} \sim 3 \times 10^2 \ [\mathrm{pc \cdot cm}^{-3}] \tag{5}\]と計算されます。 Lorimer et al., 2007の論文では\(375 \mathrm{pc \cdot cm}^{-3}\)と求めており、これと大体同じ値が求まっていることがわかります。 さらに天の川銀河内の星間空間の平均電子数密度\(n_e \sim 0.03 \mathrm{cm}^{-3}\)を用いて、距離を推定してみましょう。 簡単のため、この宇宙空間がどこまでもこの電子数密度で満たされているものとします。すると
\[\mathrm{DM} = n_e d \ \Longrightarrow \ d = \frac{\mathrm{DM}}{n_e} = 10 \ [\mathrm{kpc}] \tag{6}\]のように求まります。 実はこの推定は大雑把すぎて、少々距離が近く求まっています。 Lorimer et al., 2007では電子数密度により厳密なモデルを用い、さらにパルスを放射している天体までの距離が宇宙論的な場合のDMを用いることで、その距離を1Gpc以内としています。 いずれにしても、このFRBが近傍で発生したものであることは間違いないようです。 ちなみに、最近までに発見されているFRBの中で最も近傍にあるとされているのは、M81の方向から発生したものです。 M81は渦巻銀河であり、その距離は3.6Mpcとされています。 それに付随する球状星団内で繰り返し起こるFRBを検出したという論文が、最近Natureから出版されました。
参考文献
[1] Zhang et al., 2022, “Distribution of fast radio burst dispersion measures in CHIME/FRB Catalog 1: implications on the origin of FRBs “
[2] Lorimer et al., 2007, “A Bright Millisecond Radio Burst of Extragalactic Origin”
[3] Bhardwaj et al., 2021, “A Nearby Repeating Fast Radio Burst in the Direction of M81”
[4] Kirsten et al., 2022, “A repeating fast radio burst source in a globular cluster”
[5] AstroBaki, Dispersion measure