Table of contents
ファラデー回転 (Faraday rotation)
プラズマに外場として磁場\(\mathbf{B}_0\)が存在するときの、この磁場に沿った方向への電磁波の伝搬を考えましょう。 外場として磁場がある場合、磁場の方向が特別な方向となります。 従って、分散度量で扱った等方プラズマとは異なり、非等方プラズマとなります。
円偏光電磁波の分散関係式
任意の電磁波の電場ベクトルは、以下のように左回り・右回りの円偏光に分解して記述することができるのでした。
\[\mathbf{E} = (E_+ \boldsymbol{\epsilon}_+ + E_- \boldsymbol{\epsilon}_-) e^{-i(\omega t - \mathbf{k} \cdot \mathbf{r})} \tag{1}\] \[E_+ = \frac{1}{\sqrt{2}} (a_1 e^{-i\delta_1} -ia_2 e^{-i\delta_2}), \quad E_- = \frac{1}{\sqrt{2}} (a_1 e^{-i\delta_1} +ia_2 e^{-i\delta_2})\tag{2}\] \[\boldsymbol{\epsilon}_+ = \frac{1}{\sqrt{2}} (\boldsymbol{\epsilon}_1 + i \boldsymbol{\epsilon}_2), \quad \boldsymbol{\epsilon}_- = \frac{1}{\sqrt{2}} (\boldsymbol{\epsilon}_1 - i \boldsymbol{\epsilon}_2) \tag{3}\]ここで\(a_1, a_2\)は実数で、これはそれぞれ\(\boldsymbol{\epsilon}_1, \boldsymbol{\epsilon}_2\)の偏光ベクトル方向の振幅を表します。 \(\delta_1, \delta_2\)はれぞれ\(\boldsymbol{\epsilon}_1, \boldsymbol{\epsilon}_2\)の偏光ベクトル方向の電場の位相です。
以下では磁場に沿った方向に進む左回り円偏光電磁波が、プラズマに入射し伝搬していく場合を考えましょう。 \(\mathbf{B}_0 = B_0 \mathbf{n}\)のように書くことにします。 この\(\mathbf{n}\)は磁場の方向かつ、左回り円偏光電磁波の進行方向の単位ベクトルを表します。 左回り円偏光電磁波の場合、\(\delta = \delta_2 - \delta_1 = - \pi / 2, a_1 = a_2\)より、電場は
この左回り円偏光電磁波がプラズマ中を伝搬すると、それまで静止していたプラズマ中の電子に運動が生じます。 ここでは、電磁波により引き起こされる電子の運動の速度は光速度より十分遅いとして、非相対論の範疇で考えていきましょう。 これより、電磁波の磁場によるローレンツ力は無視されます。 さらに外部磁場強度は、電磁波の磁場強度より圧倒的に強いものとします。 電磁波は横波より、電磁波の波数ベクトル\(\mathbf{k} (=k \mathbf{n})\)に対して、常に\(\mathbf{k}\cdot \mathbf{E} =0\)が成り立ちます。 電子の運動方程式より
\[m_e \frac{d\mathbf{v}}{dt} = -e \mathbf{E} - \frac{e}{c} \mathbf{v} \times (\mathbf{B}_0 + \mathbf{B}) \simeq -e \left( \mathbf{E} + \frac{\mathbf{v}}{c} \times \mathbf{B} \right) \tag{5}\]プラズマに電磁波が入社したときの電子の速度と電流密度をそれぞれ
\[\mathbf{v} = \mathbf{v}_0 e^{-i(\omega t - \mathbf{k} \cdot \mathbf{r})}, \quad \mathbf{j} = - e n_e \mathbf{v} = - e n_e \mathbf{v}_0 e^{-i(\omega t - \mathbf{k} \cdot \mathbf{r})} \tag{6}\]のように書けます。 すると(4), (5), (6)式より
\[\begin{align} &-i m_e \omega \mathbf{v}_0 e^{-i(\omega t - \mathbf{k} \cdot \mathbf{r})} = -e \left( E_+ e^{-i (\omega t - \mathbf{k} \cdot \mathbf{r})} \boldsymbol{\epsilon}_+ + \frac{B_0}{c} e^{-i(\omega t - \mathbf{k} \cdot \mathbf{r})} \mathbf{v}_0 \times \mathbf{n} \right) \notag \\ &\Longrightarrow \ \mathbf{v}_0 = \frac{e}{im_e\omega} \left(E_+ \boldsymbol{\epsilon}_+ + \frac{B_0}{c} \mathbf{v}_0 \times \mathbf{n} \right) \tag{7} \end{align}\]を得ます。 この両辺と\(\boldsymbol{\epsilon}_+^\ast\)との内積を取ると
\[\begin{align} \mathbf{v}_0 \cdot \boldsymbol{\epsilon}_+^\ast &= \frac{e}{im_e \omega} \left\{ E_+ \boldsymbol{\epsilon}_+ \cdot \boldsymbol{\epsilon}_+^\ast + \frac{B_0}{c} (\mathbf{v}_0 \times \mathbf{n}) \cdot \boldsymbol{\epsilon}_+^\ast \right\} \underbrace{=}_{(3)} \frac{e}{im_e \omega} \left\{ E_+ + \frac{B_0}{c} \frac{1}{\sqrt{2}} (\mathbf{n} \times \boldsymbol{\epsilon}_1 - i \mathbf{n} \times \boldsymbol{\epsilon}_2) \cdot \mathbf{v}_0 \right\} \notag \\ &= \frac{e}{im_e \omega} \left\{ E_+ + \frac{B_0}{\sqrt{2} c} (\boldsymbol{\epsilon}_2 + i \boldsymbol{\epsilon}_1) \cdot \mathbf{v}_0 \right\} \underbrace{=}_{(3)} \frac{e}{im_e \omega} \left\{ E_+ + i\frac{B_0}{c} \boldsymbol{\epsilon}_+^\ast \cdot \mathbf{v}_0 \right\} \notag \\ &\Longrightarrow \ \mathbf{v}_0 \cdot \boldsymbol{\epsilon}_+^\ast = \frac{1}{1-\frac{1}{\omega} \frac{eB_0}{m_e c}} \frac{e E_+}{i m_e \omega} = \frac{eE_+}{i m_e} \frac{1}{\omega - \omega_\mathrm{ce}} \tag{8} \end{align}\]と計算されます。途中、\(\boldsymbol{\epsilon}_+ \cdot \boldsymbol{\epsilon}_+^\ast = 1\)、そしてベクトル恒等式\((\mathbf{v}_0 \times \mathbf{n}) \cdot \boldsymbol{\epsilon}_+^\ast = (\mathbf{n} \times \boldsymbol{\epsilon}_+^\ast) \cdot \mathbf{v}_0\)を用いました。さらに最後の\(\omega_\mathrm{ce} \equiv eB_0 / m_e c\)は電子サイクロトロン振動数です。 同様の計算を\(\boldsymbol{\epsilon}_-^\ast\)との内積に対しても行いましょう。 \(\boldsymbol{\epsilon}_+ \cdot \boldsymbol{\epsilon}_-^\ast = 0\)を用いると
\[\begin{align} \mathbf{v}_0 \cdot \boldsymbol{\epsilon}_-^\ast &= \frac{e}{im_e \omega} \left\{ E_+ \boldsymbol{\epsilon}_+ \cdot \boldsymbol{\epsilon}_-^\ast + \frac{B_0}{c} (\mathbf{v}_0 \times \mathbf{n}) \cdot \boldsymbol{\epsilon}_-^\ast \right\} \underbrace{=}_{(3)} \frac{e}{im_e \omega} \frac{B_0}{c} \frac{1}{\sqrt{2}} (\mathbf{n} \times \boldsymbol{\epsilon}_1 + i \mathbf{n} \times \boldsymbol{\epsilon}_2) \cdot \mathbf{v}_0 \notag \\ &= \frac{e}{im_e \omega} \frac{B_0}{\sqrt{2} c} (\boldsymbol{\epsilon}_2 - i \boldsymbol{\epsilon}_1) \cdot \mathbf{v}_0 \underbrace{=}_{(3)} -\frac{e B_0}{m_e c \omega} \boldsymbol{\epsilon}_-^\ast \cdot \mathbf{v}_0 \ \Longrightarrow \ \mathbf{v}_0 \cdot \boldsymbol{\epsilon}_-^\ast = 0 \tag {9} \end{align}\]のようになります。 すると(6), (8), (9)式、そして円偏光ベクトルについて成り立つ関係式\(\boldsymbol{\epsilon}_+ \perp \boldsymbol{\epsilon}_-\)、そして\(\boldsymbol{\epsilon}_+ \cdot \boldsymbol{\epsilon}_+^\ast = 1, \boldsymbol{\epsilon}_- \cdot \boldsymbol{\epsilon}_+^\ast = 0\)から
\[\mathbf{v} = \frac{eE_+}{i m_e} \frac{\boldsymbol{\epsilon}_+}{\omega - \omega_\mathrm{ce}} e^{-i(\omega t- \mathbf{k} \cdot \mathbf{r})} \underbrace{=}_{(4)} \frac{e}{i m_e} \frac{\mathbf{E}}{\omega - \omega_\mathrm{ce}} \tag{10}\] \[\mathbf{j} = \frac{i n_e e^2 E_+}{m_e} \frac{\boldsymbol{\epsilon}_+}{\omega - \omega_\mathrm{ce}} e^{-i(\omega t- \mathbf{k} \cdot \mathbf{r})} \underbrace{=}_{(4)} \frac{i n_e e^2}{m_e} \frac{\mathbf{E}}{\omega - \omega_\mathrm{ce}} \tag{11}\]と求まります。 一つのフーリエモードを考えると、プラズマ中でのマクスウェル方程式は
\[i \mathbf{k} \cdot \mathbf{E} = i \mathbf{k} \cdot \mathbf{B} = 0 \tag{12}\] \[i \mathbf{k} \times \mathbf{E} = \frac{i\omega}{c} \mathbf{B} \tag{13}\] \[i \mathbf{k} \times \mathbf{B} = \frac{4\pi}{c} \mathbf{j} - \frac{i\omega}{c} \mathbf{E} \tag{14}\]のようになるのでした。 これらより
\[\mathbf{k} \times (12) の左辺 = i \mathbf{k} \times (\mathbf{k} \times \mathbf{E}) = i \{ (\mathbf{k} \cdot \mathbf{E}) \mathbf{k} - k^2 \mathbf{E} \} \underbrace{=}_{(11)} -i k^2 \mathbf{E} \tag{15}\] \[\mathbf{k} \times (12) の右辺 = \frac{i\omega}{c} \mathbf{k} \times \mathbf{B} \underbrace{=}_{(13)} \frac{4\pi \omega}{c^2} \mathbf{j} - \frac{i\omega^2}{c^2} \mathbf{E} \tag{16}\]と変形できるので、(11)式を代入して整理しましょう。
\[-ik^2 \mathbf{E} = \frac{4\pi i \omega n_e e^2 }{m_e c^2 (\omega - \omega_\mathrm{ce})} \mathbf{E} - \frac{i\omega^2}{c^2} \mathbf{E} \ \Longrightarrow \ \left( k^2 + \frac{1}{c^2} \frac{\omega \omega_\mathrm{pe}^2}{\omega - \omega_\mathrm{ce}} - \frac{\omega^2}{c^2} \right) \mathbf{E} = \mathbf{0} \tag{17}\]途中、電子のプラズマ振動数\(\omega_\mathrm{pe} = \sqrt{4\pi e^2 n_e/m_e}\)を導入しました。 以上より、左回り円偏光電磁波が磁場に沿って伝搬する場合の分散関係式
\[\omega^2 = c^2 k^2 + \frac{\omega \omega_\mathrm{pe}^2}{\omega - \omega_\mathrm{ce}} \tag{18}\]が求まりました。 真空中であれば\(n_e = 0\)より、第二項がなくなり真空中の電磁波の分散関係式\(\omega = ck\)に一致することがわかります。
同様に、右回りの円偏光電磁波の場合、電子の速度は
のようになります。 (10), (19)式から、右回り・左回りに関係なく、電子は電磁波の電場ベクトルの回転方向と同じ方向に回転することがわかります。 回転の速度は右回りのときの方が、左回り円偏光のときより遅いこともわかります。 これは次のように解釈できます。 電磁波が入る前、すなわち外部磁場\(\mathbf{B}_0\)のみの場合、電子のサイクロトロン運動の回転方向は、左回り円偏光の電場の回転方向と同じです。 よって電磁波の入射は、サイクロトロン運動を助ける方向に電子に力を及ぼします。 反対に、右回り円偏光の電場の回転方向は、サイクロトロン運動の回転方向と逆となります。 これはサイクロトロン運動を妨げる結果となり、回転速度が遅くなると理解できます。
右回り円偏光電磁波の場合の計算をさらに進め、分散関係式を導出すると
のようになります。
位相差の計算
これまでの議論で求まった分散関係式を変形し、波数および位相速度を求めてみましょう。 左回り・右回り円偏光電磁波の波数をそれぞれ\(k_+, k_-\)とすると、分散関係式はひとまとめに
\[\omega^2 = c^2 k_\pm^2 + \frac{\omega \omega_\mathrm{pe}^2}{\omega \mp \omega_\mathrm{ce}} \tag{21}\]と書くことができます。 サイクロトロン振動数とプラズマ振動数の典型的な値より、電磁波の振動数においては\(\omega \gg \omega_\mathrm{ce}\)として式変形を行います。
\[\begin{align} k_\pm &= \frac{\omega}{c} \sqrt{1-\frac{\omega_\mathrm{pe}^2}{\omega^2 (1 \mp \omega_\mathrm{ce}/\omega)}} \simeq \frac{\omega}{c} \left\{ 1 - \frac{1}{2} \left( \frac{\omega_\mathrm{pe}}{\omega} \right)^2 \frac{1}{1\mp \omega_\mathrm{ce}/\omega}\right\} \notag \\ &\simeq \frac{\omega}{c} \left\{ 1 - \frac{1}{2} \left( \frac{\omega_\mathrm{pe}}{\omega} \right)^2 \left( 1 \pm \frac{\omega_\mathrm{ce}}{\omega} \right) \right\} \tag{22} \end{align}\]この結果から\(k_+ < k_-\)、そして左回り円偏光電磁波の波長\(\lambda_+ = \frac{2\pi}{k_+}\)は右回り円偏光電磁波の波長\(\lambda_- = \frac{2\pi}{k_-}\)より長くなることがわかります。 位相速度に対しても、\(\omega / k_+ > \omega / k_-\)のように、左回り円偏光電磁波の位相速度の方が大きくなります。
ここまでの議論から、電磁波が磁場に沿った方向に距離\(d\)だけプラズマ中を伝搬したときの電磁波の位相の進みは
を計算することで求まります。 \(k_+ < k_-\)より、位相の進みについても\(\phi_+ < \phi_-\)となります。 これは同じ距離だけ伝搬したとき、左回り円偏光の方が右回りに比べて、少ない位相の変化量でプラズマを進むことを示しています。 電子の速度のについての考察で見たように、右回り円偏光の場合には電子は円偏光とは逆の向きに回転運動をしようとします。 このことから、右回り円偏光電磁波は電子から抵抗を受け、位相の進みが遅くなると解釈できます。 右回りと左回りの時の位相の進みの差を\(\Delta \phi \equiv \phi_- - \phi_+\)のように書きましょう。 すると(22), (23)式より
\[\Delta \phi = \int_0^d (k_- - k_+) ds = \int_0^d \frac{\omega}{c} \left( \frac{\omega_\mathrm{pe}}{\omega} \right)^2 \frac{\omega_\mathrm{ce}}{\omega} ds = \frac{4\pi e^3}{m_e^2 c^2 \omega^2} \int_0^d n_e B_0 ds \tag{24}\]ファラデー回転 (Faraday rotation)
ここまでの結果を用いると、直線偏光電磁波に対して面白い現象が起こります。 簡単のため、二つの偏光方向に対して\(\delta_1 = \delta_2 = 0, a_1 = 0\)とします。 すなわち、入射電磁波は\(\boldsymbol{\epsilon}_2\)の方向に直線偏光していたと考えます。 するとこの直線偏光電磁波は、(1), (2), (3)式より
\[\mathbf{E} = \frac{a_2}{\sqrt{2}i} (\boldsymbol{\epsilon}_+ - \boldsymbol{\epsilon}_-) e^{-i(\omega t - \mathbf{k} \cdot \mathbf{r})} \tag{25}\]のように表記できます。 これは下図のように左回りと右回りに回転するベクトルを、全く同位相で足し合わせることで上下に振動する矢印を作ることに対応します。
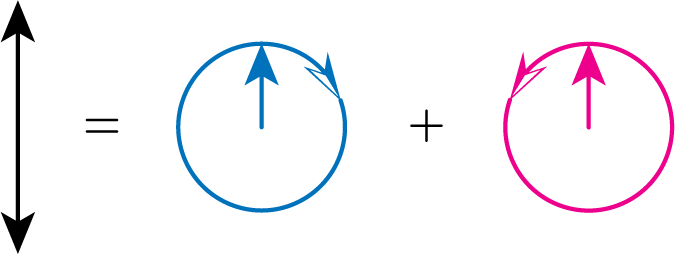
さて、先程までの議論で、もし磁場を伴うプラズマ中を左回り・右回りの円偏光電磁波が伝搬するとき、(24)式に従う位相差が発生するのでした。 すなわち次の図のように、左回り円偏光と右回り円偏光の伝搬後の位相差\(\phi\)が発生することで、偏光方向は元の方向から時計回りに\(\Delta \theta\)だけ回転した方向となります。
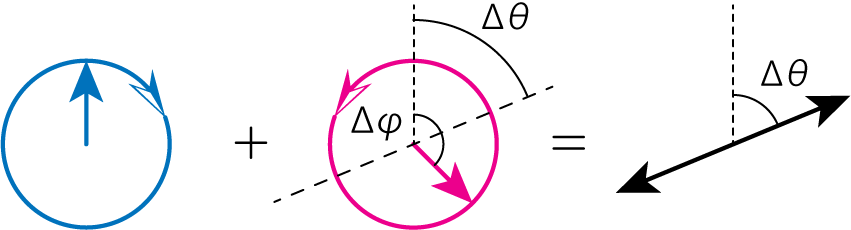
図より、\(\Delta \theta\)は
\[\Delta \theta = \frac{\Delta \phi}{2} = \frac{2\pi e^3}{m_e^2 c^2 \omega^2} \int_0^d n_e B_\parallel ds = \mathrm{RM} \lambda^2 \tag{26}\]この偏光方向の回転現象を、ファラデー回転 (Faraday rotation)と呼びます。 そしてファラデー回転を特徴づける量として、次のように回転量度 (Rotation Measure: RM)と呼ばれるものを定義します。
\[\begin{align} \mathrm{RM} &\equiv \frac{e^3}{2\pi m_e^2 c^4} \int_0^d n_e B_\parallel ds = \frac{(\hbar c)^{3/2}}{2\pi (m_e c^2)^2} \left( \frac{e^2}{\hbar c} \right)^{3/2} 10^{-6} \times 3 \times 10^{18} \int_0^{d \ \mathrm{pc}} n_e \left( \frac{B_\parallel}{1 \mu \mathrm{G}}\right) ds \notag \\ &\simeq \frac{(200 \ \mathrm{MeV \cdot fm})^{3/2} \times 3 \times 10^{12}}{6 \times (140)^{3/2} \times (0.5 \ \mathrm{MeV})^2} \int_0^{d \ \mathrm{pc}} n_e \left( \frac{B_\parallel}{1 \mu \mathrm{G}}\right) ds \notag \\ &\simeq 8 \times 10^{-5} \int_0^{d \ \mathrm{pc}} n_e \left( \frac{B_\parallel}{1 \mu \mathrm{G}}\right) ds = 0.8 \int_0^{d \ \mathrm{pc}} n_e \left( \frac{B_\parallel}{1 \mu \mathrm{G}}\right) ds \ [\mathrm{m}^{-2}]\tag{27} \end{align}\](26)式より、左辺はラジアンで無次元、右辺には\(\lambda^2\)があることから、RM自身は長さの2乗の逆数の次元を持ちます。 これは波長1mの電磁波が伝搬したときに、ファラデー回転による偏光方向の回転がRMラジアンになるものとして定義されています。
最後の係数はもう少し詳細に計算すると0.812程度になります。
例えば、観測から\(\Delta \theta\)が測定され、さらに別の観測などからDM(分散量度)が求まっていれば、\(\Delta \theta/ \mathrm{DM}\)から\(B_\parallel\)の平均的な値を算出することができます。
宇宙に一様な磁場は存在するか?
宇宙スケールの磁場
宇宙全体を貫く一様な磁場(宇宙磁場)は存在するでしょうか? もしそれが存在したとして、それはどの程度の強度だろうか、という問題を考えましょう。 これは古くはVallee, 1990などで考えられてきました。 この論文では、銀河団に所属していない\(z \leq 3.6\)までの309個の銀河・クェーサーを用いて、宇宙磁場および銀河間磁場の視線方向成分を調査しました。 もし宇宙に一様な磁場が存在するなら、遠くに行くほど(高赤方偏移銀河になるほど)RMの値が大きくなるような特別な方向が存在するはずです。
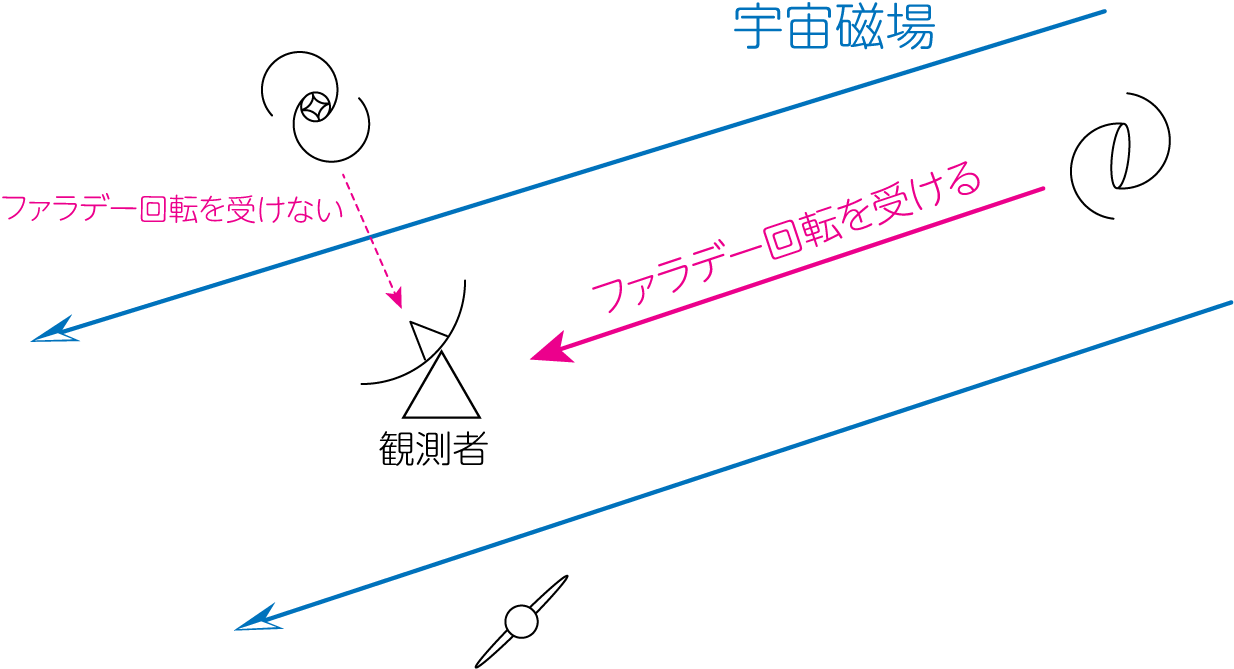
しかし、この論文の調査結果ではそのような兆候は見られませんでした。 もし一様な宇宙磁場が存在したとしても、それによるRMは\(2 \ \mathrm{rad \cdot m}^{-2}\)以下であるという上限が得られたのです。 仮に宇宙の大きさが半径100億光年の球形で、宇宙空間の平均電子密度が\(n_e \sim 2 \times 10^{-7} \ \mathrm{cm}^{-3}\)だとしましょう。 RMが一番大きくなるのは、視線方向と宇宙磁場の方向が一致した時です。 このことから
\[\begin{align} &2 \simeq 0.8 \times 2 \times 10^{-7} \left( \frac{B_\parallel}{1 \mu \mathrm{G}}\right) \times 10^{10} \times \underbrace{\frac{\overbrace{\pi \times 10^7}^{=1年} \times 3 \times 10^{10}}{3 \times 10^{18}}}_{=1光年を\mathrm{pc}換算} \ \Longrightarrow \ \left( \frac{B_\parallel}{1 \mu \mathrm{G}}\right) \sim 4 \times 10^{-3} \notag \\ &\Longrightarrow \ B_\parallel \sim 4 \ [\mathrm{nG}] \tag{28} \end{align}\]と求まります。 大雑把な見積もりですが、もし宇宙に一様な磁場が存在しても、その大きさは\(\mathrm{nG} (=10^{-9} \mathrm{G})\)より小さいということが示されました。 宇宙一様磁場が存在すると、その方向はこの宇宙において特別な方向となります。 すなわち等方の仮定をおいている宇宙論モデルとは相容れないものとなるのです。 この宇宙一様磁場の観測から、このような一様等方でない宇宙モデルに対して制限をかけることができます。 さらには、このような宇宙磁場は初期宇宙での量子ゆらぎなどから発生するものと考えられており、その理論によって初期にできる種磁場の大きさは異なります。 ここから初期宇宙モデルに制限をかけることも可能となります。 宇宙磁場は本当に存在するのか、あるとしてそれはどのような大きさか、またそれはどのように発生するのかは未解明の最先端分野と言えるでしょう。
余談: 各天体に付随した磁場や手前にある天体の効果はどうやって取り除く?
ここまでは私たち観測者と天体の間に一様磁場しかない、理想的な状態で話を進めてきました。 しかし実際の宇宙空間には、観測ターゲットである天体の手前に別の天体が存在し、それによる影響を受けます。 さらには、そのターゲット天体自身も磁場を持つことが考えられるため、各天体固有のRM成分を持つはずです。 ではどのようにこれを除去し、宇宙一様磁場の情報を引き出せば良いのでしょうか。
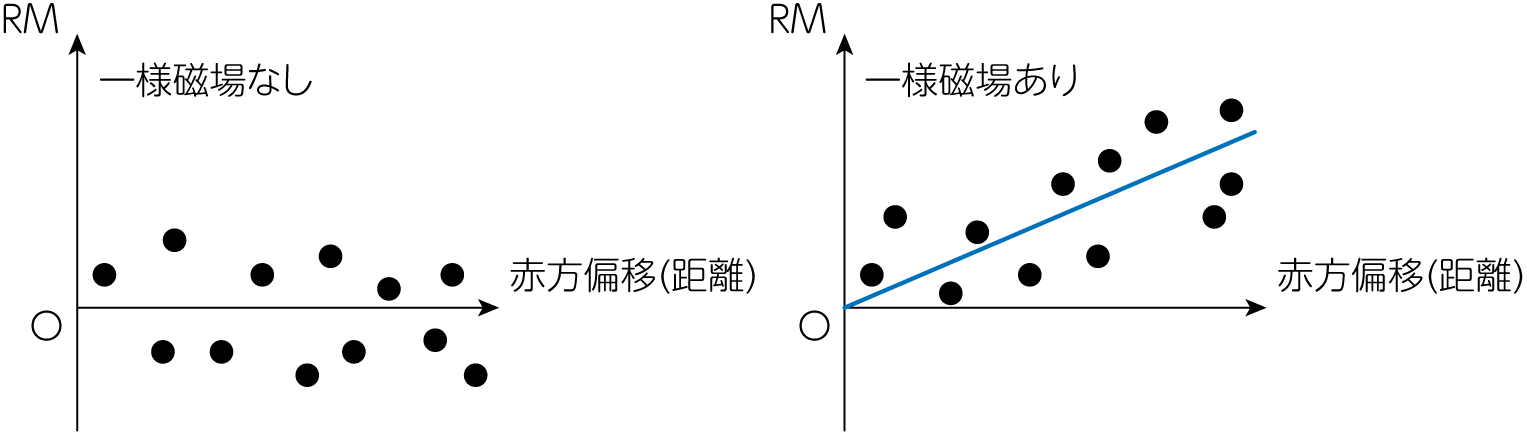
それには各天体で求められたRMの相関を見ます。 天体の持つ磁場や観測ターゲット天体の固有磁場は無相関なはずです。 よってもし一様磁場がなければ、観測した天体に関してRMを平均すると0に近い値になります。 逆に一様磁場が存在する場合、ある方向に着目したときに、距離に比例してRMが大きくなっていくような振る舞いが見えることになります。
大規模構造スケールの磁場
先程の例は\(z \leq 3.6\)までの非常に大きな(Gpcの)スケールの場合です。 次はそれよりもいくぶん小さい、Mpcスケールの大局的に揃った銀河間空間磁場についても触れておきましょう。 Lee et al., 2009では、SDSSのデータとNRAO VLAサーベイデータによるファラデー回転測定値を用いた研究を行っています。 それによると、背景となる電波源の位置から1Mpc/h以上離れた高密度領域を通過してきた電波は、そのRMが著しく大きいことが確認されたのです。
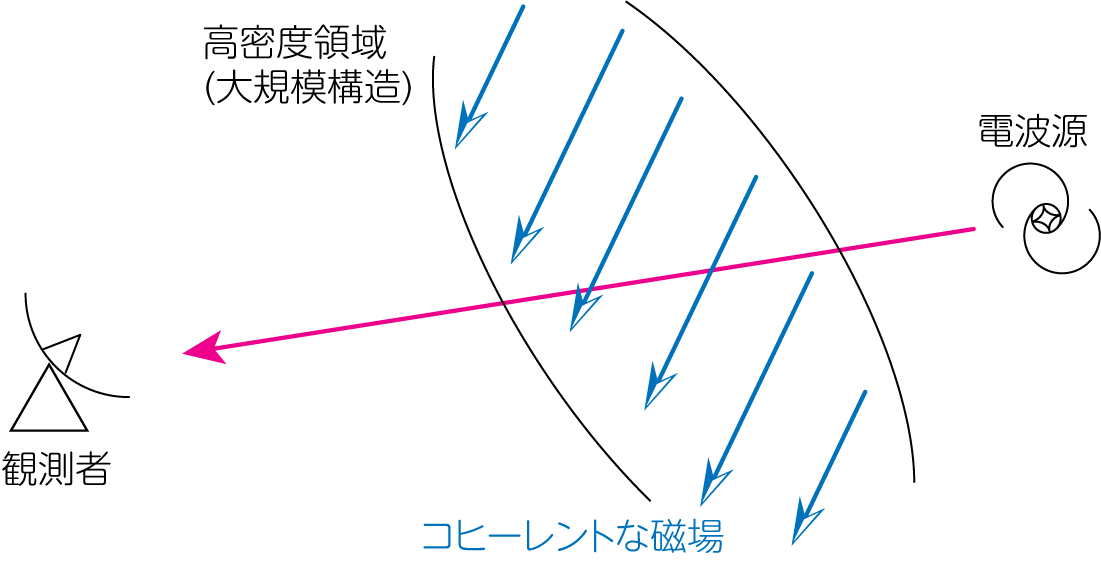
このことから、その高密度領域には1Mpc/hにわたってコヒーレントな磁場が存在し、その大きさが30nGであると結論づけました。 ファラデー回転を用いた観測から、宇宙大規模構造に大局的な磁場が存在することが示唆されたのです。
参考文献
[1] Vallee, 1990, “Detecting the Largest Magnets: The Universe and the Cluster of Galaxies”
[2] Lee et al., 2009, “Detection of Large-Scale Cosmic Magnetic Fields”
[3] 天文学辞典, ファラデー回転