Table of contents
完全電離水素プラズマ中でのRutherford散乱とSpitzer熱伝導率
1個の電子を陽子に向かって入射させたRutherford散乱から、多数の電子を入射させた場合に話を発展させることで散乱断面積という概念を学びました。次はプラズマ中ではこの散乱がどのようになるかを見てみましょう。
デバイ遮蔽による効果
プラズマ中ではデバイ遮蔽により、クーロンポテンシャルは無限遠まで到達せず、デバイ長\(\lambda_D\)と呼ばれる距離の範囲内にしか影響を及ぼさなくなります。すなわちデバイ長よりも遠くですれ違う電子は散乱を受けないことになります。衝突パラメータがデバイ長と等しくなるような位置を通り過ぎる電子はわずかに散乱を受け、このときの散乱角を\(\theta_\mathrm{min} (\ll 1)\)とします。
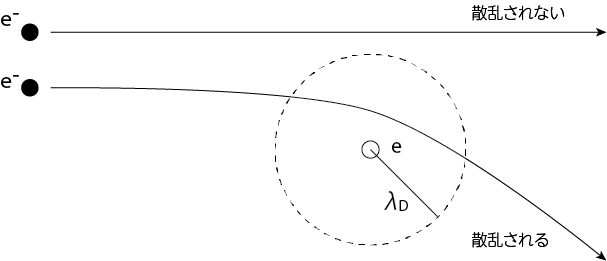
運動量交換衝突断面積
\(\theta\)方向に散乱された電子の運動量の\(x\)成分は\(m_e V_0\)から\(m_e V_0 \cos \theta\)に変化しています。運動量保存から電子が陽子に受け渡した\(x\)方向の運動量は
\[p_x = m_e V_0 - m_e V_0 \cos \theta = m_e V_0 (1- \cos \theta)\]です。当然ながら、\(y\)方向にも運動量のやりとりをしています。しかし、今は電子と陽子が入り乱れたプラズマ中を考えているため、多数の電子が様々な衝突パラメータで陽子に向けて撃ち込まれることを考えると、陽子が獲得する\(y\)方向の運動量は平均すると0になると考えてよいでしょう。
すると運動量交換の衝突断面積は、ラザフォード散乱の微分散乱断面積の式に\((1-\cos \theta)\)の重みをかけたものを全立体角積分したものとなります。今、散乱方向は\(\theta_\mathrm{min} \leq \theta \leq \pi\)より
のようにかけます。
運動量交換にかかる典型的な時間
ラザフォード散乱において衝突パラメータ\(b\)がちょうどデバイ長\(\lambda_D\)のとき
\[\frac{m_e V_0^2}{e^2} \lambda_D = \cos \frac{\theta_\mathrm{min}}{2}\]が成り立つのでした。\(\cot \frac{\theta_\mathrm{min}}{2} \simeq \frac{2}{\theta_\mathrm{min}}\)、さらに右辺において\(\frac{1}{2} m_e V_0^2 \simeq k_B T\)のように、運動エネルギーと熱エネルギーの間で等分配が成り立っているとすると
\[\frac{2}{\theta_\mathrm{min}} \simeq \frac{2 k_B T}{e^2} \sqrt{\frac{k_B T}{4\pi e^2 n_e}} = 4\pi n_e \left( \frac{k_B T}{4\pi e^2 n_e}\right)^{3/2} \simeq \Lambda_c \tag{3}\]ここで\(n_e\)は電子の個数密度です。最右辺に現れた\(\Lambda_c = n_e \lambda_D^3\)は、デバイ長を半径とする球内にいる電子の数、すなわちデバイ遮蔽を引き起こす(協調現象をになっている)電子数です。
Λcはlog内に現れるため、係数などは大雑把に考えています。
(1), (3)式より
\[\sigma_p \simeq \pi \left( \frac{2e^2}{m_e V_0^2} \right)^2 \ln \Lambda_c \tag{4}\]となります。この運動量を交換する指標となる散乱断面積\(\sigma_p\)を用いて、電子が陽子に運動量を受け渡す(すなわち衝突したと見なせる)のにかかる典型的な時間(mean free time)を\(\tau_{ep}\)とすると
\[\tau_{ep} = \frac{\mathrm{mean \ free \ path}}{V_0} = \frac{1}{n_e \sigma_p V_0} \simeq \frac{1}{n_e V_0} \frac{m_e^2 V_0^4}{4\pi e^4} \frac{1}{\ln \Lambda_c}\]です。先ほどと同様に\(\frac{1}{2} m_e V_0^2 \simeq k_B T\)を用いると
\[\tau_{ep} = 2^{3/2} \frac{m_e^{1/2} }{4 \pi e^4} \frac{(k_B T)^{3/2}}{n_e \ln \Lambda_c} = \frac{2^{3/2}}{4\pi} \frac{(m_e c^2)^{1/2}}{c} \left( \frac{\hbar c}{c^2} \right)^2 \frac{(k_B T)^{3/2}}{n_e \ln \Lambda_c} \tag{5}\]ここで物理定数や単位換算として
\[m_e c^2 \sim 0.5 [\mathrm{MeV}], \quad \frac{e^2}{\hbar c} \sim \frac{1}{137}, \quad \hbar c \sim 197 [\mathrm{Mev} \cdot \mathrm{fm}], \quad k_B T \simeq \left(\frac{T}{10^4 [K]} \right) [\mathrm{eV}], \quad 1 [\mathrm{fm}] = 10^{-13} [\mathrm{cm}]\]を用いると
\[\tau_{ep} \simeq 0.27 \frac{T^{3/2}}{n_e \ln \Lambda_c} \tag{6}\]となります。\(\Lambda_c\)がどのような値になろうとも、その依存性は\(\log\)でしか存在しません。\(\ln \Lambda_c\)はCoulomb logarismと呼び、その値はおよそ\(5 \sim 20\)程度です。
4つの場合の衝突頻度
これまでは陽子をまとにして電子が撃ち込まれる場合の系を考えてきました。しかし、実際のプラズマでは電子と陽子は入り乱れています。よって
- 陽子をまとにして電子が撃ち込まれる
- 電子をまとにして陽子が撃ち込まれる
- 電子をまとにして電子が撃ち込まれる
- 陽子をまとにして陽子が撃ち込まれる
の4つの衝突を考えなければ、プラズマ中の散乱を完全に理解したとは言えないでしょう。ではこれら4パターンの運動量交換時間はどのようになるでしょうか。衝突頻度から考えていきましょう。
(5)式より
です。このことから、陽子をまとにして陽子が撃ち込まれる場合の衝突頻度は
\[\nu_{pp} = \sqrt{\frac{m_e}{m_p}} \nu_{ep} \tag{8}\]と類推できます。
次に電子をまとにして電子が撃ち込まれる場合を考えましょう。(7)式に「陽子がまとである」という情報が入っていないことから、この場合の衝突頻度は、陽子をまとにして電子が撃ち込まれる場合と同じと考えられます。よって
です。
最後に電子をまとにして陽子が撃ち込まれる場合の衝突頻度を考えましょう。電子が陽子に入射する場合、(1)式の運動量交換断面積の計算では\(1-\cos \theta\)の重み付けをしていました。よって陽子が電子に入射する場合にはここにさらに変更が加わります。熱平衡状態のとき
さらに運動量保存を考え、電子が\(\theta\)方向に散乱されるときに陽子は\(\theta_p\)方向に散乱されるとすると
\[m_e v_e - m_p v_p = m_e v_e \cos \theta - m_p v_p \cos \theta_p \ \Longrightarrow \ m_e v_e (1-\cos \theta) = m_p v_p (1-\cos \theta_p)\]ここに先程の式を用いることで
\[1-\cos \theta_p = \sqrt{\frac{m_e}{m_p}} (1-\cos \theta)\]のようになります。よって「陽子のまとに電子が撃ち込まれる」場合の重み付けが\(1-\cos \theta\)だったならば、「電子のまとに陽子が撃ち込まれる」場合の重み付けは(10)式でなければなりません。陽子と電子の質量比はおよそ1800倍なので、陽子の運動量変化はわずかです。陽子の運動量は電子の運動量よりもはるかに大きいため、電子によって陽子が散乱を受けても、1回の散乱ではほとんど運動量変化を感じないという直感に一致する結果になっています。よって
\[\nu_{pe} = \sqrt{\frac{m_e}{m_p}} \nu_{pp} \tag{10}\](7), (8), (9), (10)式から、それぞれの運動量交換頻度は
\[\nu_{ep} : \nu_{ee} : \nu_{pp} : \nu_{pe} = 1 : 1 : \sqrt{\frac{m_e}{m_p}} : \frac{m_e}{m_p} \tag{11}\]とわかります。(11)式より電子の衝突頻度(\(\nu_{ep}, \nu_{ee}\))は陽子の衝突頻度(\(\nu_{pp}, \nu_{pe}\))に比べて大きいことがわかります。もし非平衡プラズマが存在すると、まず電子が衝突を繰り返して熱平衡に落ち着きます。その後に陽子・イオンが衝突を繰り返して熱平衡になります。電子が熱平衡になったとしてイオンは熱平衡になるまでにさらに時間がかかるため、これらを別成分とみなして2流体でプラズマを研究する試みもされています。
Spitzer熱伝導率
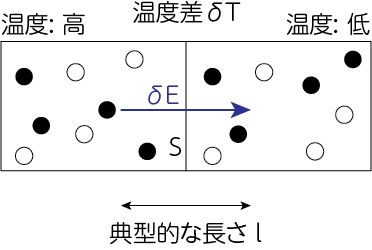
温度が\(\delta T\)だけ異なる2つの完全電離水素プラズマがある面を境にして接していたとしましょう。境界面の面積を\(S\)とします。温度差があるため熱伝導が起こりますが、(11)式で示したように陽子はあまり衝突を起こさないため、ここでは熱伝導が電子の熱運動によってのみもたらされるものとします。\(\tau\)だけ時間が経過したときに温度が高い方から低い方へ流れ込んだエネルギー量を\(\delta E\)とすると、単位時間あたりに流れ込むエネルギーは
\[\frac{\delta E}{\tau} = \frac{n_e k_B \delta T \cdot S \cdot \ell}{\tau}\]です。ここで\(\kappa_\mathrm{sp}\)をSpitzerの熱伝導率と呼びます。熱伝導率は単位長さ・単位温度・単位時間あたりに伝わるエネルギー量、として定義されます。
\(\tau = \tau_{ep}\)とすれば、\(\ell\)は電子の平均自由行程\(\ell_e = (n_e \sigma_p)^{-1}\)に一致します。\(\ell\)が考えている系よりも十分小さければ\(\delta T \simeq \ell |\nabla T|\)のようにかけるため、熱伝導によるエネルギーフラックス\(q\)は
です。\(\tau_{ep}= \ell_e / V_0\)より
\[\kappa_\mathrm{sp} = \frac{n_e k_B \ell_e^2 V_0}{\ell_e} = \frac{k_B V_0}{\sigma_p} \underbrace{=}_{(4)} \frac{\sqrt{2} k_B^{7/2}}{\pi e^4 m_e^{1/2}} \frac{T^{5/2}}{\ln \Lambda_c}\]係数部分のみを計算しましょう。
\[\begin{aligned} &\frac{\sqrt{2}}{\pi} \frac{\hbar^2 c^2}{e^4} \frac{1}{\hbar^2 c^2} \left( \frac{10^4 k_B}{10^4} \right)^{7/2} \frac{c}{(m_e c^2)^{1/2}} \sim \frac{\sqrt{2}}{\pi} 140^2 \frac{1}{200^2 \mathrm{MeV}^2 \ \mathrm{fm}^2} \frac{1 \mathrm{eV}^{7/2}}{10^{14}} \frac{3 \cdot 10^{10}}{0.5^{1/2} \mathrm{MeV}^{1/2}} \\ &\sim \frac{\sqrt{2}}{\pi} \frac{2 \cdot 10^4}{4 \cdot 10^4 \cdot 10^{12} \cdot 10^{-26}} \frac{1}{10^{14}} \frac{3 \cdot 10^{10}}{\frac{1}{\sqrt{2}} 10^3 \mathrm{eV}^{1/2}} \sim \frac{2}{3} \frac{2 \cdot 10^4 \cdot 3 \cdot 10^{10}}{4 \cdot 10^4 \cdot 10^{12} \cdot 10^{-26} \cdot 10^{14} \cdot 10^{3}} \cdot \underbrace{1 \mathrm{eV}}_{1.6 \cdot 10^{-12}} \\ &\sim 1.6 \times 10^{-5} \end{aligned}\]以上より
\[\kappa_\mathrm{sp} \simeq 1.6 \times 10^{-6} \left( \frac{10}{\ln \Lambda_c}\right) T^{5/2} \ [\mathrm{erg \ K^{-1} \ cm^{-1} \ s^{-1}}] \tag{12}\]となります(正確には\(1.84 \times 10^{-6}\)程度です)。
これはSpitzer熱伝導率と呼ばれ、星間物質中で起こる熱伝導を考えるときによく用いられる値です。
参考文献
- Spitzer, “Physics of Fully Ionized Gases”
- 田中基彦, 西川恭治, “高音プラズマの物理学”