Table of contents
与えられた場における荷電粒子の運動
ここでは、プラズマの運動論現象を理解するための基本となる、与えられた電磁場の中での荷電粒子の運動についてまとめました。
一様電磁場中での粒子の運動
例題
時間変化がないかつ空間的に一様な磁場中では、荷電粒子は磁場に巻き付く、一定の螺旋運動を行います。 しかし、そこに電場も加わると、この荷電粒子の運動はどのようになるでしょうか。 荷電粒子の質量・電荷・速度をそれぞれ\(m, q, \mathbf{v}\)とします。 一様磁場は\(\mathbf{B}_0 = B_0 \mathbf{e}_z\)のように、\(z\)軸方向を向いているとし、さらに一様電場は\(\mathbf{E}_0 = E_x \mathbf{e}_x + E_z \mathbf{e}_z\)のように\(x-z\)平面にとるとしましょう。 荷電粒子の運動方程式
\[m \frac{d \mathbf{v}}{dt} = q \left( \mathbf{E} + \frac{\mathbf{v}}{c} \times \mathbf{B} \right) \tag{1}\]より、\(x, y, z\)成分の式はそれぞれ
\[\frac{dv_x}{dt} = \frac{q}{m} E_x + \omega_c v_y \tag{2}\] \[\frac{dv_y}{dt} = - \omega_c v_x \tag{3}\] \[\frac{dv_z}{dt} = \frac{q}{m} E_z \tag{4}\]となります。 途中、サイクロトロン振動数を\(\omega_c \equiv \frac{qB_0}{mc}\)のように置きました。 (4)式は、\(z\)方向への等加速度運動を表しています。 (2), (3)式の両辺を時間で微分すると
\[\frac{d^2v_x}{dt^2} = \omega_c \frac{dv_y}{dt} \underbrace{=}_{(3)} - \omega_c^2 v_x \tag{5}\] \[\frac{d^2 v_y}{dt^2} = - \omega_c \frac{dv_x}{dt} \underbrace{=}_{(2)} - \omega_c^2 \left(v_y + \frac{c E_x}{B_z}\right) \ \Longrightarrow \ \frac{d^2 }{dt^2} \left( v_y + \frac{cE_x}{B_z}\right) = - \omega_c^2 \left( v_y + \frac{cE_x}{B_z}\right) \tag{6}\]を得ます。 (5), (6)式から
\[v_x = v_{0} e^{i \omega_c t}, \quad v_y = i v_{0} e^{i \omega_c t} - \frac{cE_x}{B_z} \tag{7}\]が解とわかります。 このように、この電磁場中を運動する荷電粒子はサイクロトロン運動をしつつ、その旋回中心(guiding center)は\(-y\)方向に運動をすることがわかりました。
旋回中心のドリフト: 電場ドリフト
より一般的な方向を持つ電場・磁場の場合について、このドリフト運動を求めてみましょう。 先程の例題から分かるように、このような場合の運動は磁場によるサイクロトロン運動と一定のドリフト速度\(\mathbf{v}_\mathrm{E}\)の和で表されることがわかります。 さらに例題からも分かるように、このドリフト速度ベクトルは常に電場と磁場に垂直とします。 サイクロトロン一周期での時間平均を取ると、(1)式は
\[\langle \frac{d\mathbf{v}}{dt} \rangle = \frac{q}{m} \left( \mathbf{E}_0 + \frac{\mathbf{v}_\mathrm{E}}{c} \times \mathbf{B}_0\right) = 0 \tag{8}\]のようになります。 ここで、磁場によるサイクロトロン運動の速度と加速度の一周期の時間平均はゼロとしました。 この式の両辺に、磁場\(\mathbf{B}_0\)をベクトル積としてかけてみましょう。
\[\frac{q}{m} \left(\mathbf{E}_0 \times \mathbf{B}_0 + \frac{1}{c} (\mathbf{v}_\mathrm{E} \times \mathbf{B}_0) \times \mathbf{B}_0\right) = \frac{q}{m} \mathbf{E}_0 \times \mathbf{B}_0 + \frac{q}{mc} \underbrace{(\mathbf{v}_\mathrm{E} \cdot \mathbf{B}_0)}_{\mathbf{v}_\mathrm{E} \perp \mathbf{B}_0} - \frac{q B_0^2}{mc} \mathbf{v}_\mathrm{E} \tag{10}\]以上より
\[\mathbf{v}_\mathrm{E} = \frac{c \mathbf{E}_0 \times \mathbf{B}_0}{B_0^2} \tag{11}\]のように、電場によるドリフト運動を求めることができました。 (11)式で重要なことは、\(\mathbf{v}_\mathrm{E}\)が\(m, q, v_0\)に依存せず、場の量のみで決まることです。 よって、電子とイオンは同じ方向に同じ速度でドリフト運動を行うため、正味の電流は発生しません。
直感的には、この電場ドリフトは次のように理解することができます。 磁場の影響により、荷電粒子は電場方向に直線的に加速され続けることはできず、そのうち電場による減速を受けることになります。 加速部分ではラーモア半径が大きくなり、減速部分ではラーモア半径が小さくなります。 これにより、下図のような電場にも磁場にも垂直な方向へのドリフトが生じるのです。
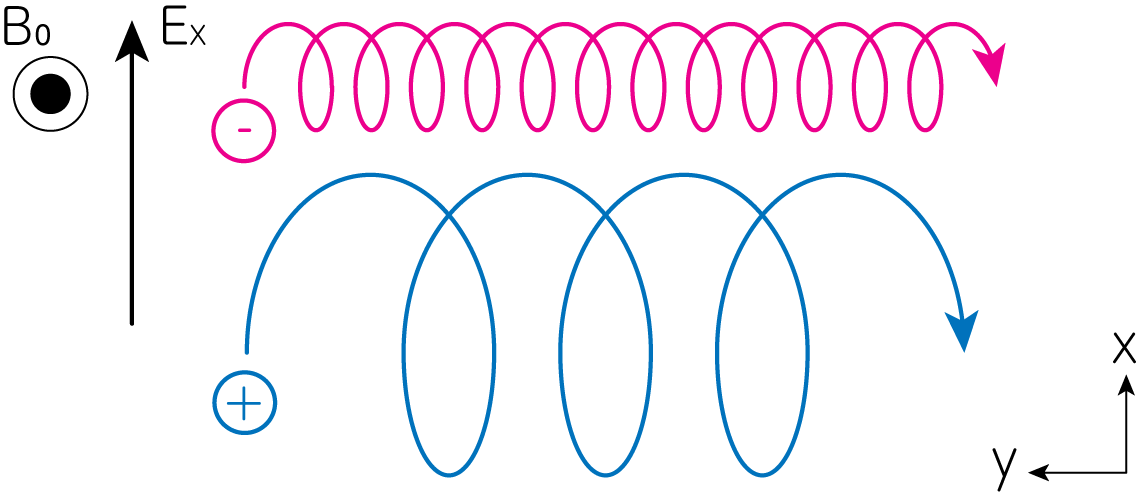
一般的な力によるドリフト
運動方程式(1)の\(q \mathbf{E}\)を一般的な力\(\mathbf{F}\)に置き換えることで、(11)式の電場ドリフトを他の力の場合に適用することができます。 このようにして、\(\mathbf{F}\)による旋回中心のドリフトは
\[\mathbf{v}_\mathrm{f} = \frac{c}{q} \frac{\mathbf{F} \times \mathbf{B}_0}{B_0^2} \tag{12}\]となります。 特に重力\(m \mathbf{g}\)の場合
\[\mathbf{v}_\mathrm{g} = \frac{mc}{q} \frac{\mathbf{g} \times \mathbf{B}_0}{B_0^2} = \frac{\mathbf{g} \times \hat{\mathbf{b}}_0}{\omega_c} \tag{13}\]のようになります。 途中、磁場方向の単位ベクトルを\(\hat{\mathbf{b}}_0 = \mathbf{B}_0 / B_0\)としました。 またこれを重力ドリフトと呼ぶこともあります。 このドリフトは\(\mathbf{F}, \mathbf{B}\)の両方に垂直という点では、先程の\(\mathbf{v}_\mathrm{E}\)と同じです。 しかし、(13)式の途中からも分かる通り、\(\mathbf{v}_\mathrm{g}\)は電荷の正負によってドリフト方向が変化します。 重力のもとでイオンと電子は逆方向にドリフトし、正味の電流密度
\[\mathbf{j} = q n \mathbf{v}_\mathrm{g} = (m_i + m_e) c n \frac{\mathbf{g} \times \mathbf{B}_0}{B_0^2} \tag{14}\]がプラズマ中に存在することになります。 ここで\(m_i, m_e\)はそれぞれイオンと電子の質量、\(n\)は荷電粒子の個数密度です。
時間的に変化する電場存在下での荷電粒子の運動
例題
\(\mathbf{E}\)が空間的には一様ですが、ゆっくりと時間変化する場合について考えましょう。 なお磁場はこれまでと同じく、一様かつ時間に依存せず一定で、\(z\)方向を向いているとします。 \(x\)軸を\(\mathbf{E}\)に沿ってとり
\[\mathbf{E} = E_0 e^{i \omega t} \mathbf{e}_x \tag{15}\]とします。 ただし時間変化は十分遅いとして、\(\omega \ll \omega_c\)であるとします。 すると(2), (3)式より
\[\ddot{v}_x = \frac{q}{m} \dot{E}_x + \omega_c \dot{v}_y = \frac{iq\omega}{m} E_x + - \omega_c^2 v_x = - \omega_c^2 \left( v_x - \frac{i\omega}{\omega_c} \frac{cE_x}{B_0} \right) = -\omega_c^2 (v_x - v_\mathrm{p}) \qquad \left(v_\mathrm{p} \equiv \frac{i\omega}{\omega_c} \frac{cE_x}{B_0} \right)\tag{16}\] \[\ddot{v}_y = - \omega_c \dot{v}_x = - \omega_c \left( \frac{q}{m} E_x + \omega_c v_y\right) = -\omega_c^2 \left( v_y - v_\mathrm{E} \right) \tag{17}\]のようになります。 (17)式の\(v_\mathrm{E}\)は、(11)式の電場ドリフト速度です。 (16), (17)式の解が、\(\omega \ll \omega_c\)の仮定のもとで
\[v_x = v_0 e^{i\omega_c t} + v_\mathrm{p}, v_y = i v_0 e^{i\omega_c t} + v_\mathrm{E} \tag{18}\]となることを示しましょう。 これらの時間2階微分をとると
\[\ddot{v}_x = - v_0 \omega_c^2 e^{i \omega_c t} - \omega^2 v_\mathrm{p} = - \omega_c^2 v_x + (\omega_c^2 - \omega^2) v_\mathrm{p}\] \[\ddot{v}_y = -i v_0 \omega_c^2 e^{i\omega_c t} - \omega^2 v_\mathrm{E} = -\omega_c^2 v_y + (\omega_c^2 - \omega^2) v_\mathrm{E}\]のようになりますが、\(\omega^2 \ll \omega_c^2\)の仮定により、これらが(16), (17)式と一致することがわかります。 ここまでの議論から分かるように、電場の時間変化によって、旋回中心の新たなドリフト\(v_\mathrm{p}\)が加わっていることがわかります。
分極ドリフト
先程は電場が\(E_0 e^{i \omega t}\)のように、ゆっくりと振動する場合のみを考えました。 ここでは、より一般的な場合のドリフトについて考えてみましょう。 ただし、ここでも電場の時間変化は十分ゆっくりであるとします。
まずは先程の例題も踏まえて、この場合にどのような現象が起こるかを考察します。 電場の存在により、荷電粒子の旋回中心は電場ドリフトを行います。 しかし、電場の時間変化により、電場ドリフトの大きさも同じ速さで変化します。 これは電場ドリフト方向に等価な力が働いていることを意味します。 一般的な力におけるドリフトの式(12)を見てみると、この力によって新たに磁場に垂直な方向へドリフトが生じることがわかります。
以上の考察から粒子の速度を、電場が存在しないときのサイクロイド運動速度\(\mathbf{v}_0\)、電場ドリフト速度\(\mathbf{v}_\mathrm{E}\)、そして新しいドリフト\(\mathbf{v}_\mathrm{p}\)に分けることにしましょう。
これを(1)式に代入すると
\[m (\dot{\mathbf{v}}_0 + \dot{\mathbf{v}}_\mathrm{E}) = q \mathbf{E} + \frac{q}{c} (\mathbf{v}_0 + \mathbf{v}_\mathrm{E} + \mathbf{v}_\mathrm{p}) \times \mathbf{B}_0 \tag{20}\]のようになります。 途中、\(\mathbf{v}_\mathrm{p}\)の時間変化はさらに高次の微少量であるとして、無視しました。 この式において、\(\dot{\mathbf{v}}_0\)を含む左辺の第一項と、右辺の第二項がつりあいます。 また電場ドリフトに対応する右辺第一項と第三項がつりあうため、最終的に
\[m \dot{\mathbf{v}}_\mathrm{E} = \frac{q}{c} \mathbf{v}_\mathrm{p} \times \mathbf{B}_0 \tag{21}\]を得ます。 この式の両辺に磁場ベクトル\(\mathbf{B}_0\)をかけてベクトル積を作ると
\[(\mathbf{E} \times \mathbf{B}_0) \times \mathbf{B}_0 = \underbrace{(\mathbf{E} \cdot \mathbf{B}_0)}_{\mathbf{E} \perp \mathbf{B}_0} \mathbf{B}_0 - B_0^2 \mathbf{E}, \quad (\mathbf{v}_\mathrm{p} \times \mathbf{B}_0) \times \mathbf{B}_0 = \underbrace{(\mathbf{v}_\mathrm{p} \cdot \mathbf{B}_0)}_{\mathbf{v}_\mathrm{p} \perp \mathbf{B}_0} \mathbf{B}_0 - B_0^2 \mathbf{v}_\mathrm{p}\]より、最終的に
\[\mathbf{v}_\mathrm{p} = \frac{mc^2}{qB_0^2} \frac{d\mathbf{E}_\perp}{dt} = \frac{c}{\omega_c B_0} \frac{d \mathbf{E}_\perp}{dt} \tag{22}\]を得ます。 これを分極ドリフト (polarization drift)と呼びます。 分母にサイクロトロン振動数\(\omega_c\)が入っていることから分かるように、主にイオンについてのドリフトであることがわかります。 したがって、磁場に垂直な電場の大きさが時間的にゆっくりと変化するときは、その電場方向に正味の電流が発生します。 分極ドリフトは、アルヴェーン波などの磁気流体波の伝搬を、イオン運動を通して支えます。 それだけでなく、波動を介しての磁場を横切る方向の異常イオン拡散などに重要な働きをしています。
非一様な磁場中での粒子の運動
磁場勾配ドリフト
ここでは電場は存在せず、その代わりに磁場の大きさが空間的にゆるやかに変化する場合を考えましょう。 このとき、1サイクロトロン周期中でラーモア半径が変化します。 すなわち強磁場側ではラーモア半径が小さく、低磁場側ではラーモア半径が大きくなります。 このことから、粒子の軌道は磁場および磁場強度勾配の両方に垂直な方向へ、一定速度でズレていくことになります。

磁場の空間分布をテイラー展開を用いて
\[\mathbf{B} (\mathbf{r}) \simeq \mathbf{B}_0 + (\mathbf{r} \cdot \nabla) \mathbf{B}_0 \tag{23}\]のように書くことで、非一様磁場の効果を取り入れましょう。 ここで、\(\mathbf{r}\)は旋回中心からの位置ベクトルを表し、さらに第二項は第一項に比べて十分小さいとします。 これを運動方程式(1)に代入すると
\[\frac{d\mathbf{v}}{dt} = \frac{q}{mc} \{\mathbf{v} \times \mathbf{B}_0 + \mathbf{v} \times (\mathbf{r} \cdot \nabla) \mathbf{B}_0\} \tag{24}\]となります。 第一項が第二項に比べて大きいことから、粒子の運動が磁場による旋回運動\(\mathbf{v}_0\)と、そこからのズレ\(\mathbf{v}_1\)として表現されるとすると
\[\frac{d\mathbf{v}_1}{dt} = \frac{q}{mc} \{ \mathbf{v}_1 \times \mathbf{B}_0 + \mathbf{v}_0 \times (\mathbf{r}_0 \cdot \nabla) \mathbf{B}_0\} \tag{25}\]のようになります。 途中、\((\mathbf{r}_0 \cdot \nabla) \mathbf{B}_0\)は一次の微小量であり、これに\(\mathbf{v}_1\)がかかったものは無視しました。 この式をサイクロトロン運動の一周期に渡って平均しましょう。 冒頭の議論から、荷電粒子は強磁場側と低磁場側を行き来することになるため、左辺の\(\frac{d \mathbf{v}_1}{dt}\)の平均はゼロになると予想されます。 以上より
\[\mathbf{v}_\mathrm{B} \times \mathbf{B}_0 + \langle \mathbf{v}_0 \times (\mathbf{r}_0 \cdot \nabla) \mathbf{B}_0 \rangle = 0 \qquad (\mathbf{v}_\mathrm{B} \equiv \langle \mathbf{v}_1 \rangle)\tag{26}\]を得ます。 \(\mathbf{v}_0, \mathbf{r}_0\)は、磁場\(\mathbf{B}_0\)によるサイクロトロン運動から出てくることを思い出しましょう。 そして今、磁場強度は\(x\)方向に変化するとすると
\[\begin{align} \langle \mathbf{v}_0 \times (\mathbf{r}_0 \cdot \nabla) \mathbf{B}_0 \rangle &= -r_L^2 \omega_c (\langle \cos^2 \omega_c t\rangle \mathbf{e}_x+ \langle \sin \omega_c t \cos \omega_c t\rangle \mathbf{e}_y) \frac{\partial B_0}{\partial x} = - \frac{1}{2} r_L^2 \omega_c \frac{\partial B_0}{\partial x} \mathbf{e}_x \notag \\ &= - \frac{1}{2} r_L^2 \omega_c \nabla \mathbf{B}_0 \tag{27} \end{align}\]となります。 ここで\(r_L\)はラーモア半径です。 これを(26)式に代入し、その両辺を\(\mathbf{B}_0\)とのベクトル積を取れば
\[\mathbf{v}_\mathrm{B} = \frac{v_0^2}{2 \omega_c} \frac{\mathbf{B}_0 \times \nabla \mathbf{B}_0}{B_0^2} = \frac{c W_\perp}{q B_0} \frac{\mathbf{B}_0 \times \nabla \mathbf{B}_0}{B_0^2} \tag{28}\]を得ます。 これを磁場勾配ドリフト (gradient-B drift)と呼びます。 途中の\(W_\perp\)は磁場に垂直な方向の荷電粒子の運動エネルギーです。 このことから磁場勾配ドリフトでは、主に磁場に垂直な方向に高エネルギーの荷電粒子が磁場勾配ドリフトを起こし、正味の電流がもたらされます。
磁力線湾曲ドリフト
ここまで磁力線は直線的であるとしてきましたが、ここでは磁力線が曲率半径\(R\)で空間的に湾曲している場合を考えましょう。
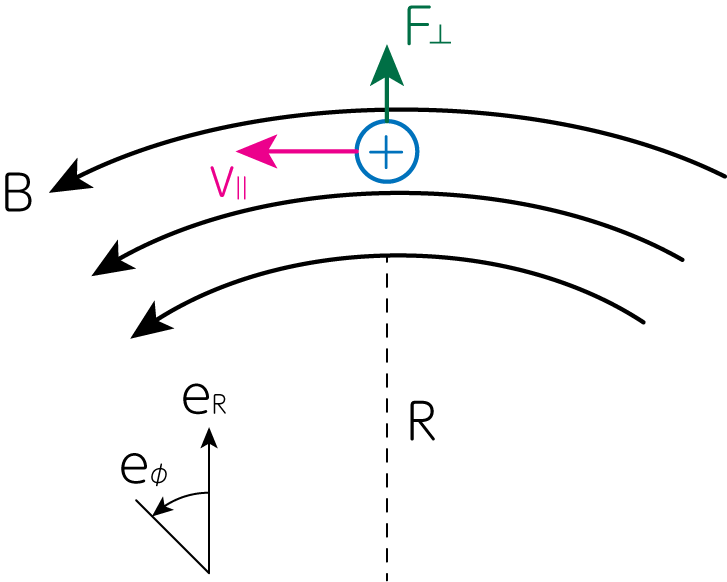
荷電粒子は磁力線を横切れず、磁力線に沿って運動を行います。 するとこの粒子には、曲率中心から外向きの遠心力が働きます。
\[\mathbf{F}_\perp = \frac{m v_\parallel^2}{R} \mathbf{e}_R \tag{29}\]ここで\(\mathbf{e}_R\)は、曲率中心から外向きの単位ベクトルです。 この遠心力を、外場\(\mathbf{F}\)によるドリフト速度の一般式(12)に代入すると
\[\mathbf{v}_\mathrm{c} = \frac{c}{q} \frac{m v_\parallel^2}{R B_0} \mathbf{e}_R \times \hat{\mathbf{b}}_0 = \frac{v_\parallel^2}{R \omega_c} \mathbf{e}_R \times \hat{\mathbf{b}}_0 \tag{30}\]を得ます。 これを磁力線湾曲ドリフト (curvature drift) と呼びます。
次に、湾曲ドリフトとともに必ず存在する磁場勾配ドリフトを、曲率半径方向の\(\vert B \vert\)の減少を考慮して計算してみましょう。 マクスウェル方程式より、真空中では\(\nabla \times \mathbf{B} = \mathbf{0}\)です。 また磁場は\(\varphi\)成分しか持たないとすると
より
\[\vert B \vert \propto \frac{1}{R}, \quad \frac{\nabla \vert B \vert}{\vert B \vert} = - \frac{\mathbf{e}_R}{R} \tag{32}\]となります。 これと(28)式を用いると
\[\mathbf{v}_\mathrm{B} = - \frac{v_\perp^2}{2\omega_c} \frac{\mathbf{B} \times \frac{\mathbf{e}_R}{R^2}}{B} = \frac{v_\perp^2}{2\omega_c} \frac{\mathbf{e}_R \times \mathbf{B}}{R B} \tag{33}\]より、これと湾曲ドリフトとを合わせて
\[\mathbf{v}_\mathrm{mag} = \frac{v_\parallel^2 + \frac{1}{2} v_\perp^2}{R \omega_c} (\mathbf{e}_R \times \hat{\mathbf{b}}) \tag{34}\]のように書くことができます。 ここで\(v_\parallel, v_\perp\)はそれぞれ、磁力線に平行方向と垂直方向の粒子の速度です。
このようなドリフトは、熱核融合プラズマで重要な働きをします。 核融合プラズマを閉じ込める目的で単純な磁場トーラスを用いるとき、温度や磁場をどのように調整しても、粒子はトーラスの外部にドリフトしてしまうことがわかります。
非一様な電場中での粒子の運動
先程までは非一様な磁場による効果について考察しましたが、ここでは磁場は一様で、電場が非一様な場合について考えてみましょう。 簡単のため、\(\mathbf{E}\)は\(x\)方向を向いており、さらに\(y\)方向に沿っては正弦的に変化する \(\mathbf{E} \equiv E_0 \cos (ky) \mathbf{e}_x\)の形とします。。
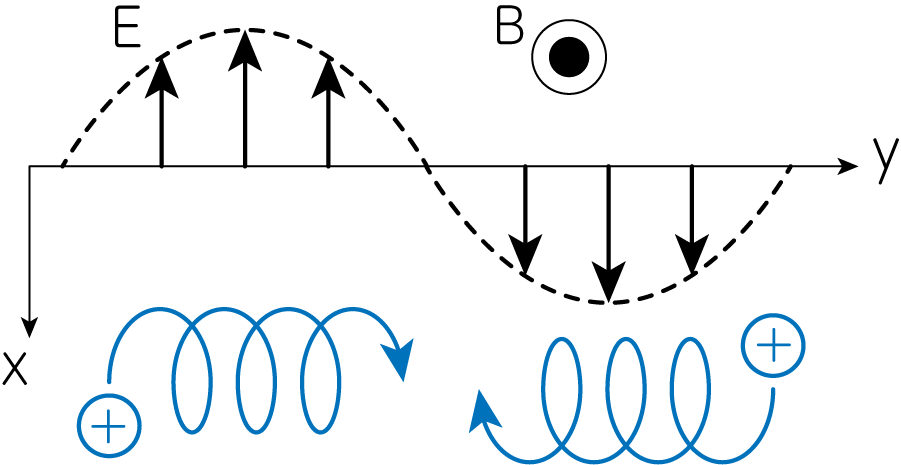
磁場に垂直な\(x, y\)方向の運動方程式は
\[\dot{v}_x = \omega_c v_y + \frac{q}{m} E_x(y), \quad \dot{v}_y = - \omega_c v_x \tag{35}\]です。 これらの時間微分から
\[\ddot{v}_x = - \omega_c^2 v_x \tag{36}\] \[\ddot{v}_y = - \omega_c^2 v_y - \omega_c^2 \frac{cE_x(y)}{B} \tag{37}\]を得ます。 粒子の位置における電場\(E_x(y)\)を求めるためには、求めようとしている粒子の軌道を知る必要があります。 もし電場が弱ければ、電場がない場合の軌道と摂動的な軌道を足し合わせた解析が可能となります。 そこで、まずは電場がない場合の軌道をみてみましょう。 するとこれは磁場によるサイクロトロン運動に他ならないため
\[y = y_0 \pm r_L \cos \omega_c t \tag{38}\]とわかります。 ここで\(y_0\)は荷電粒子の初期位置です。 よって(37)式から
\[\ddot{v}_y = - \omega_c^2 v_y - \omega_c^2 \frac{cE_0}{B} \cos \{k (y_0 \pm r_L \cos \omega_c t)\} \tag{39}\]のようになります。 第二項において
\[\begin{align} \cos \{k (y_0 \pm r_L \cos \omega_c t)\} &= \cos (k y_0) \cos (k r_L \cos \omega_c t) \mp \sin (k y_0) \sin (k r_L \cos \omega_c t) \notag \\ &\underbrace{\approx}_{k r_L \ll 1} \cos (k y_0) \left(1 - \frac{1}{2} k^2 r_L^2 \cos^2 \omega_c t \right) \mp \sin (ky_0) k r_L \cos \omega_c t \end{align}\]のように整理しましょう。 途中の\(k r_L \ll 1\)の近似は、電子やイオンのラーモア半径が、電場の波長よりも十分短い場合に対応します。 プラズマにおいては、だいたいはこの近似でも十分です。 結果を予想して、\(\omega_c\)の旋回と、定常的なドリフト\(v_\mathrm{E}\)の重ね合わせのような解を探してみましょう。 1周期にわたる平均操作をとることで、旋回運動を取り除きます。 すると(39)式から
\[\begin{align} &\langle \ddot{v}_y \rangle = - \omega_c^2 \langle v_y \rangle - \omega_c^2 \frac{cE_0}{B} \langle \cos \{k (y_0 \pm r_L \cos \omega_c t)\}\rangle = - \omega_c^2 \langle v_y \rangle - \omega_c^2 \frac{cE_0}{B} \cos (ky_0) \left(1 - \frac{1}{4} k^2 r_L^2 \right) = 0 \notag \\ &\Longrightarrow \ \langle v_y \rangle = - \frac{cE_x(y_0)}{B}\left(1 - \frac{1}{4} k^2 r_L^2 \right)\tag{40} \end{align}\]を得ます。 また\(v_x\)に関しては、(36)式から\(\langle v_x \rangle = 0\)は明らかです。 (40)式で\(k \rightarrow 0\)(波長無限大の極限)を取ると、(11)式の電場ドリフトに一致することがわかります。 すなわちこれは電場の非一様性により、電場ドリフトが補正を受けたと考えることができるのです。
\[\mathbf{v}_\mathrm{E} = \frac{c \mathbf{E} \times \mathbf{B}}{B^2} \left(1 - \frac{1}{4} k^2 r_L^2 \right) \tag{41}\](41)式で現れた補正\(-\frac{1}{4} k^2 r_L^2\)の意味を考えてみましょう。 例えば、電場\(\mathbf{E}\)が最大となる点を旋回中心に持つ荷電粒子は、\(\mathbf{E}\)のより弱い領域で運動時間の大部分を費やします。 したがって、その平均的なドリフトは、旋回中心で求まる\(E/ B\)よりも小さくなります。 \(\mathbf{E}\)が単調に増加・減少しているような場所では、荷電粒子はある時には強い電場を感じますが、その反対部分では弱い電場を感じることになります。 このため、\(\mathbf{v}_\mathrm{E}\)の修正は相殺されます。 このことから、修正項は\(\mathbf{E}\)の2階微分に依存することがわかります。 解析的に式を求める上で仮定した電場の正弦分布では、その空間の2階微分は常に負となります。 任意の\(\mathbf{E}\)の変化に対しては、\(ik\)を\(\nabla\)で置き換えれば良いでしょう。
\[\mathbf{v}_\mathrm{E} = \left(1 + r_L^2 \nabla^2 \right) \frac{c \mathbf{E} \times \mathbf{B}}{B^2} \tag{42}\]この第二項を有限ラーモア半径効果と呼びます。
プラズマ中でこのドリフトが発生したとき、イオンのラーモア半径の方が電子よりもとても大きいため、一般に\(\mathbf{v}_\mathrm{E}\)はプラズマを構成する荷電粒子の種類に関係します。 プラズマ中に電荷密度の偏りが生じると、これにより生じる電場がイオンと電子を分離し、また別の電場を作り出します。 このように作られた第二の電場が、第一の電場をを助長するようなフィードバック機構がもし存在するなら、\(\mathbf{E}\)は再現なく成長し続け、プラズマは不安定となります。 このように荷電粒子のドリフトにより発生する不安定性を、ドリフト不安定性と呼びます。 磁場勾配ドリフト(28)式において\(\nabla \rightarrow ik\)のように置き換えると、磁場勾配ドリフトは\(k\)に比例することがわかります。 それに比べ、(42)式の修正項は\(k^2\)に比例することから、この効果は\(k\)が比較的大きい(電場変化を表す長さが比較的短い)場合に重要となります。 このことからドリフト不安定性は、微視的不安定性と呼ばれるものに分類されます。
参考文献
[1] 田中基彦, 西川恭治, “高温プラズマの物理学”
[2] Chen, 内田 岱二郎(訳), “プラズマ物理入門”
[3] 宮本健郎, “プラズマ物理・核融合”
[4] 小野高幸, 三好良純, “太陽地球圏”
[5] 加藤鞆一, “核融合はなぜむずかしいか”