Table of contents
恒星内で起こる熱核反応
恒星内部で起こる核融合反応は、熱核反応と呼ばれます。 それはガスを構成する粒子(原子核)が熱運動で飛び回っている間に衝突を起こし、核反応を起こすというものです。
原子核の結合エネルギー (nuclear binding energy)
粒子a, bが反応を起こし、粒子cと光子\(\gamma\)になったとしましょう。
\[a + b \ \longrightarrow \ c + \gamma\]この核反応が起こったときのエネルギー収支を考えましょう。 粒子a, b, cの静止質量をそれぞれ\(m_a, m_b, m_c\)と書き、粒子の運動エネルギーは静止質量エネルギー\(mc^2\)に比べて非常に小さい(非相対論的)とすると、この反応でのエネルギー保存は
\[(m_a + m_b - m_c) c^2 = E_\gamma \tag{6.3.1}\]のように表すことができます。 ここで\(E_\gamma\)は光子のエネルギーを表します。 反応前後での静止質量の差が、光子のエネルギーとして放出されます。 光子はMeVのオーダーのエネルギーを持つガンマ線ですが、発生するとすぐに周りのガスに吸収され、粒子の熱運動のエネルギーと低いエネルギーの光に変えられます。 すなわち、核融合反応では反応前後での静止質量の差が熱エネルギーとなります。
原子核の静止質量は、その質量数(原子核内の陽子と中性子の数)とその結合エネルギー\(E_\mathrm{B}\)により決まります。 原子核内の陽子数と中性子数をそれぞれ\(Z, N\)と書くと、原子核の静止質量\(m_\mathrm{i}\)は
と書かれます。 ここで\(m_\mathrm{p}, m_\mathrm{n}\)はそれぞれ陽子と中性子の質量を表します。 核融合反応では、質量数は保存されます。 すると
\[m_a + m_b = (Z_a + Z_b) m_\mathrm{p} + (N_a + N_b) m_\mathrm{n} - \frac{E_{\mathrm{B}, a} + E_{\mathrm{B}, b}}{c^2} \simeq (A_a + A_b) m_\mathrm{p} - \frac{E_{\mathrm{B}, a} + E_{\mathrm{B}, b}}{c^2} \quad (m_\mathrm{p} \simeq m_\mathrm{n})\] \[m_c = (A_a + A_b) m_\mathrm{p} - \frac{E_{\mathrm{B}, c}}{c^2}\]のようになります。 ここで\(A_a, A_b\)はそれぞれ原子核\(a, b\)の質量数です。 以上より、(6.3.1)式は
\[E_\gamma = E_{\mathrm{B}, c} - (E_{\mathrm{B}, a} + E_{\mathrm{B}, b}) \tag{6.3.2}\]のように変形されます。 この式は、結合エネルギーの差が核融合反応によりエネルギーとして出てくることを意味しています。 次の図は、1核子あたりの結合エネルギー\(E_\mathrm{B} / A\)を質量数に対して描画したものです。
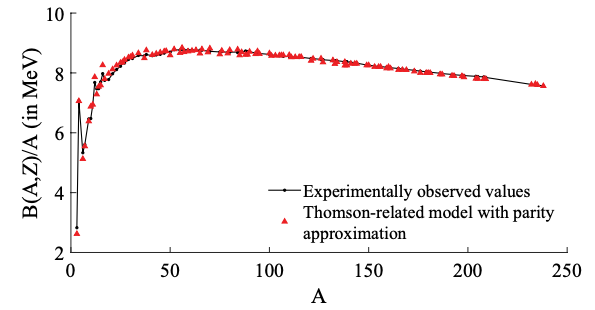
1核子あたりの結合エネルギーは質量数とともに急激に増加し、\(A (=N+Z) \gtrsim 12\)では\(\sim 8 \mathrm{MeV}\)程度となります。 その値は質量数が\(\sim 60\)の鉄グループの原子核で最高となり、それより重い原子核に対してはなだらかに減少しています。 そのため水素からヘリウム・炭素などと、鉄までの重い原子核が作られていく核融合反応が起こるとエネルギーが発生し、これが恒星中でのエネルギー源となります。
核反応率 (nuclear reaction rates)
2つの原子核\(a, b\)が、単位体積・単位時間あたりに起こす核反応\(r_{ab}\) (単位体積あたりの核反応率)を定式化しましょう。
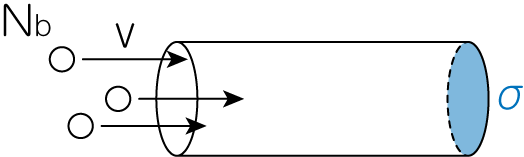
上図のように、1個の原子核\(a\)に数密度\(N_b\)の原子核\(b\)が相対速度\(v\)で飛び込んでいく状況を考えましょう。 運動エネルギー\(\mathcal{E}\)で起こる\(a, b\)間の反応の反応断面積を\(\sigma_{ab} (\mathcal{E})\)とすると、\(N_b v \sigma_{ab}\)が原子核\(a\)1つあたり・単位時間あたりに反応する原子核\(b\)の粒子数となります。 単位体積あたりの原子核\(a\)の数が\(N_a\)であることから、単位時間・単位体積あたりに反応する原子核\(a, b\)の粒子数は\(\frac{N_a N_b}{1+\delta_{ab}} v \sigma_{ab}\)と書くことができます。 ここで\(\delta_{ab}\)は原子核\(a, b\)が同じ種類の原子核のとき1、そうでないとき0となる関数です。 そして分母の\(1+\delta_{ab}\)は、\(a=b\)のときに\(1/2\)とすることで、ボンド数を補正・ダブルカウントを防ぐためのものです。 以上から、原子核がマクスウェル・ボルツマン分布\(f(\mathcal{E})\)に従って運動している場合の、原子核反応率は
\[r_{ab} = \frac{N_a N_b}{1+\delta_{ab}} \int_0^\infty \sigma_{ab} (\mathcal{E}) v(\mathcal{E}) f(\mathcal{E}) d\mathcal{E} = \frac{N_a N_b}{1+\delta_{ab}} \langle \sigma v \rangle_{ab} \rangle \tag{6.3.3}\]のように表されます。 ここで\(\langle \sigma v \rangle_{ab}\)は\(\sigma_{ab} v(\mathcal{E})\)の平均を表しています。 速度のマクスウェル・ボルツマン分布\(v^2 \exp \left\{ - \frac{m_{ab} v^2}{2k_B T}\right\} dv\) (\(m_{ab}\)は原子核\(a, b\)の換算質量)を運動エネルギー\(\mathcal{E} = \frac{1}{2} m_{ab} v^2\)に変換し、その規格化しましょう。
\[d\mathcal{E} = m_{ab} v dv = \sqrt{2 m_{ab} \mathcal{E}} dv\]より
\[f(\mathcal{E}) = \frac{\sqrt{\mathcal{E}} e^{-\mathcal{E} / (k_B T)} d\mathcal{E}}{\int_0^\infty \sqrt{\mathcal{E}} e^{-\mathcal{E} / (k_B T)} d\mathcal{E}} = \frac{2}{\sqrt{\pi} (k_B T)^{3/2}} e^{-\mathcal{E} / (k_B T)} \sqrt{\mathcal{E}} d\mathcal{E} \tag{6.3.4}\]続いて、反応断面積\(\sigma_{ab}\)について考えてみましょう。 原子核は正の電荷を持っているため、反応を起こそうと近づく原子核間にはクーロン反発力が働きます。 質量数\(A\)を持つ原子核の半径は、近似的に
\[R_\mathrm{n} \approx 1.2 \times 10^{-13} A^{1/3} \ [\mathrm{cm}] \tag{6.3.5}\]のように表されます。 原子核の\(a, b\)の質量数をそれぞれ\(A_a, A_b\)とし、電荷をそれぞれ\(Z_a, Z_b\)と書くと、それらが反応を起こすために越えなければならない静電エネルギー障壁 (Coulomb barrier)は
\[E_\mathrm{C} \approx \frac{Z_a Z_b e^2}{1.2 \times 10^{13} (A_a^{1/3} + A_b^{1/3})} \ [\mathrm{erg}] \approx 1.2 \frac{Z_a Z_b}{A_a^{1/3} + A_b^{1/3}} \ [\mathrm{MeV}] \tag{6.3.6}\]のようになります。 \(1 \mathrm{eV} \sim 10^4 \mathrm{K}\)より、熱運動でこの障壁を越えるには\(10^{10} \mathrm{K}\)程度が必要とわかります。 これに対し、主系列星およびヘリウム燃焼段階の恒星の中心温度は\(10^7 \sim 10^8 \mathrm{K}\)となっています。 従って、恒星中心で核反応が起きるためには、原子核は量子力学のトンネル効果により静電エネルギー障壁を透過する必要があります。 \(E_\mathrm{C} \gg \mathcal{E}\)のときのトンネル降下による透過率\(P_\ell (\mathcal{E})\)は、WKB近似により求められ
\[P_\ell (\mathcal{E}) \propto e^{-2\pi \eta_{ab}} \quad \left( \eta_{ab} \equiv \frac{Z_a Z_b e^2}{\hbar v } \approx 0.157 Z_a Z_b \left( \frac{A_{ab}}{\mathcal{E} \ [\mathrm{MeV}]}\right)^{1/2}\right) \tag{6.3.7}\]のように表されます。 ここで\(A_{ab}\)は原子核\(a, b\)の、原子質量単位の換算質量を表します。 次の図は、原子核反応の概念図です。
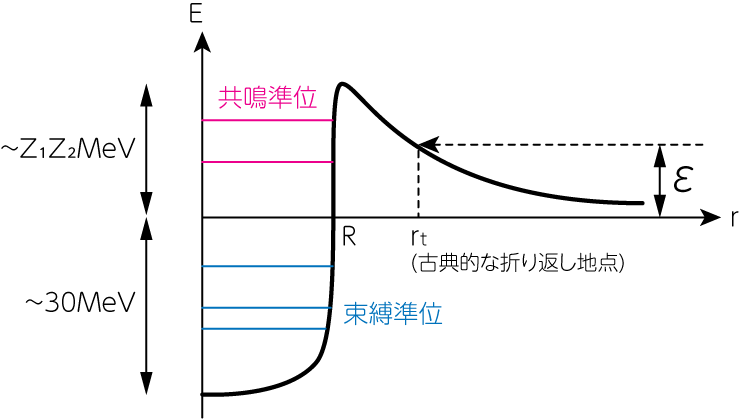
半径\(r_0\)以内では核力によるポテンシャルより、2つの入射粒子の複合状態ができます。 エネルギーが負の準位は束縛された準位であり、最低エネルギー準位の状態が、安定な原子核の状態を表します。 エネルギーが正の準位は共鳴準位と呼ばれ、この準位には2つの原子核分離した状態とトンネル効果により結合した状態です。 そして共鳴準位にある複合核は、有限の寿命で崩壊し、核融合が行われます。
反応断面積\(\sigma_{ab}\)はこの静電エネルギー障壁の透過率\(P_\ell (\mathcal{E})\)に比例するとともに、2つの原子核\(a, b\)の相対速度に対するドブロイ波長 (DeBroglie wavelength)の2乗に比例します (これは面積に対応します。) 相対速度に対する運動量を\(p\)とすると、このドブロイ波長は
より、\(\lambda^2 \propto 1/ \mathcal{E}\)に比例することがわかります。
反応断面積\(\sigma_{ab}\)のこれらのエネルギー依存性を具体的に表して
のように書く習慣があります。 この\(S(\mathcal{E})\)は、天体物理的S因子 (Astrophysical S-factor)と呼ばれるものです。 \(\sigma_{ab}\)がエネルギーとともに急激に変化するのに対し、\(S(\mathcal{E})\)はエネルギー\(\mathcal{E}\)に対してゆっくり変化する量となる、という特徴があります。 一般に、恒星内部で起こる核反応での相対運動のエネルギー\(\mathcal{E}\)は、反応断面積を計測する実験で用いられるエネルギーに比べて非常に低いことが知られています。 そのため、外挿により恒星内部での熱核反応に対する反応断面積を得る必要があります。 それにはエネルギー依存性の小さい天体物理的S因子を使う方が都合が良いため、このような習慣があります (共鳴反応が起こる場合には\(S(\mathcal{E})\)にも強いエネルギー依存性があるため特別な扱いが必要ですが、ここでは簡単のために非共鳴的な反応のみを考えることにします。)
(6.3.8)式を(6.3.3)式に代入しましょう。 \(v = \sqrt{2 \mathcal{E} / m_{ab}}\)を用いて
のようになります。 ここで
\[\zeta \equiv \frac{\pi \sqrt{2m_{ab}} Z_a Z_b e^2}{\hbar} \quad \left( 2\pi \eta_{ab} = \frac{\zeta}{\sqrt{\mathcal{E}}}\right) \tag{6.3.10}\]です。 (6.2.9)式の被積分関数にある\(e^{-\frac{\mathcal{E}}{k_B T}}\)は、マクスウェル分布から来たものです。 これは典型的なエネルギー\(k_B T\)より大きいエネルギーを持つ粒子数が、急激に減少することに対応します。 一方、\(e^{- \zeta / \sqrt{\mathcal{E}}}\)はクーロン障壁に対する透過確率からきたもので、エネルギーが増加するに連れて大きくなります。 これら2つの関数と、そしてそれらの積である被積分関数を次の図に表しました。
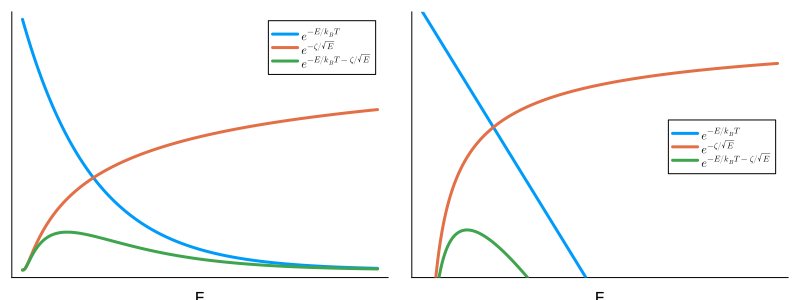
右図は左図の縦軸を対数にしたものを表しています。 この図に表されているように、これら2つの関数の席は、2つの関数のすその交わるあたりのエネルギーに鋭いピークを持ちます。 このピークはガモフピーク(Gamow-peak)と呼ばれています。 このピークの性質に基づく近似を用い、(6.3.9)式の積分を解析に実行しましょう。
ピークの位置\(\mathcal{E}_0\)は、\(-\frac{\mathcal{E}}{k_B T} - \frac{\zeta}{\sqrt{\mathcal{E}}}\)が最大となるところなので
のように得られます。 ここから\(\exp \left( - \frac{\mathcal{E}}{k_B T} - \frac{\zeta}{\sqrt{\mathcal{E}}}\right)\)のピーク値を求めましょう。
\[\exp \left( - \frac{\mathcal{E}_0}{k_B T} - \frac{\zeta}{\sqrt{\mathcal{E}_0}}\right) = \exp \left( - \frac{\mathcal{E}_0}{k_B T} - \frac{2 \mathcal{E}_0^{3/2}}{k_B T \sqrt{\mathcal{E}_0}}\right) = e^{-\frac{3\mathcal{E}_0}{k_B T}} \equiv e^{-\tau} \tag{6.3.12}\]ここで\(\tau\)は
\[\tau \equiv \frac{3\mathcal{E}_0}{k_B T} = 3 \left( \frac{\zeta^2}{4k_B T}\right)^{1/3} \propto \frac{m_{ab}^{1/3} (Z_a Z_b)^{2/3}}{T^{1/3}} \tag{6.3.13}\]です。
(6.3.9)式の積分では、ガモフピーク付近のエネルギーに対する被積分関数の値しか寄与しないと近似しましょう。 そのため、エネルギーに対してゆっくり変化する関数\(S(\mathcal{E})\)は\(S_0 \equiv S (\mathcal{E}_0)\)として積分の外に出すことができます。 そして\(g(\mathcal{E}) = - \frac{\mathcal{E}}{k_B T} - \frac{\zeta}{\sqrt{\mathcal{E}}}\)を\(\mathcal{E} = \mathcal{E}_0\)の周りでテイラー展開すると
のように近似されます。 これを(6.3.9)式の積分に代入すると
\[\begin{align} \int_0^\infty \exp \left( -\frac{\mathcal{E}}{k_B T} - \frac{\zeta}{\sqrt{\mathcal{E}}}\right) d\mathcal{E} &\simeq e^{-\tau} \int_{-\mathcal{E}_0}^\infty \exp \left\{ - \frac{\tau}{4} \frac{(\mathcal{E} - \mathcal{E}_0)^2}{\mathcal{E}_0^2}\right\} \underbrace{d(\mathcal{E} - \mathcal{E}_0)}_{=dx} \notag \\ &\simeq e^{-\tau} \int_{-\infty}^\infty e^{-\frac{\tau}{4\mathcal{E}_0^2} x^2} dx = 2 \sqrt{\frac{\pi}{\tau}} e^{-\tau} \mathcal{E}_0 \tag{6.3.15} \end{align}\]のように積分できます。 途中、被積分関数は\(\mathcal{E} \sim \mathcal{E}_0\)でしか大きな値を持たないため、積分の下限を\(-\mathcal{E}_0\)から\(-\infty\)に変えました。 このように積分が近似的に実行できたため、(6.3.9)式は最終的に
\[\begin{align} \langle \sigma v \rangle &\simeq S_0 \sqrt{\frac{8}{\pi m_{ab}}} \frac{1}{(k_B T)^{3/2}} 2 \sqrt{\frac{\pi}{\tau}} e^{-\tau} \mathcal{E}_0 = \frac{4}{3} \sqrt{\frac{2}{m_{ab}}} S_0 \frac{\tau^2}{\sqrt{k_B T \tau^3}} e^{-\tau} \notag \\ &= \frac{8}{9} \sqrt{\frac{2}{3m_{ab}}} \frac{S_0}{\zeta} \tau^2 e^{-\tau} \simeq \frac{8\hbar}{3^{5/2} \pi m_{ab} e^2} \frac{S_0}{Z_a Z_b} \tau^2 e^{-\tau} \tag{6.3.16} \end{align}\]のように計算されます。 温度依存性は\(\tau^2 e^{-\tau} \ (\tau \propto T^{-1/3})\)に含まれています。 ここでは\(\tau^2\)よりも\(e^{-\tau}\)の方が温度変化に対して急激に変化するため、核反応率は温度が高いほど大きくなります。 また2つの原子核の電荷の積が大きいほど、(高いクーロン障壁にために)高い温度でしか核反応が起こりません。
1回の核反応で放出されるエネルギーを\(Q\)と書くと、単位時間・単位質量あたりに放出されるエネルギー\(\epsilon_\mathrm{n}\)は(6.3.3)式より
のように表されます。 \(\epsilon_\mathrm{n}\)の温度依存性は
\[\begin{align} \left( \frac{\partial \ln \epsilon_\mathrm{n}}{\partial \ln T}\right)_\rho &\propto \left[ \frac{\partial}{\partial \ln T} \left( 2 \ln \tau - \tau \right) \right]_\rho \propto \left[ \frac{\partial}{\partial \ln T} \left( -\frac{2}{3} \ln T - \tau \right) \right]_\rho \notag \\ &\propto - \frac{2}{3} - \left( \frac{\partial \tau}{\partial \ln T}\right)_\rho \underbrace{\propto}_{\ln T \propto -3 \tau} - \frac{2}{3} + \frac{\tau}{3} \tag{6.3.18} \end{align}\]となります。 恒星の中の状態では多くの場合\(\tau \gg 1\)なので、核反応によるエネルギー発生率は温度に非常に敏感となります。
電子による遮蔽効果 (electron screening)
ここまでは原子核\(a, b\)の間の静電エネルギーを電荷\(Z_a, Z_b\)とだけがあるとして表してきました。 しかし密度が高い場合には、原子核\(a, b\)の間にいる電子による電荷の遮蔽効果を補正する必要があります。 電荷\(Z_\mathrm{i} e\)を持つイオン(原子核)の数密度を\(N_\mathrm{i}\)とし、電子の数密度を\(N_\mathrm{e}\)と書くと、静電ポテンシャル\(\phi\)のもとでは
\[N_\mathrm{i} = N_\mathrm{0i} e^{-\frac{Z_\mathrm{i} e \phi}{k_B T}}, \quad N_\mathrm{e} = N_\mathrm{0e} e^{\frac{e\phi}{k_B T}} \tag{6.3.19}\]のように表現されます。 ここで\(N_\mathrm{0i}, N_\mathrm{0e}\)はそれぞれ、静電場の効果を無視したときのイオンと電子の数密度を表します。 ガスが電気的に中性であるという条件から
\[Z_\mathrm{i} N_\mathrm{0i} = N_\mathrm{0e} \tag{6.3.20}\]が成り立ちます。 静電ポテンシャル\(\phi\)はポアソン方程式
\[\nabla^2 \phi = -4\pi (N_\mathrm{i} Z_\mathrm{i}-N_\mathrm{e}) e \tag{6.3.21}\]に従います。 静電エネルギーが熱エネルギー (粒子の運動エネルギー)に比べて非常に小さい場合 \(\left( \frac{Z_\mathrm{i} e\phi}{k_B T} \ll 1\right)\)だけを考えましょう。 すると(6.3.19)式が
\[\begin{align} N_\mathrm{i} Z_\mathrm{i} - N_\mathrm{e} &\simeq N_\mathrm{0i} Z_\mathrm{i} \left( 1 - \frac{Z_\mathrm{i} e \phi}{k_B T}\right) - N_\mathrm{0e} \left( 1 + \frac{e \phi}{k_B T}\right) \notag \\ &\underbrace{\simeq}_{(6.3.20)} - (N_\mathrm{i} Z_\mathrm{i}^2 + N_\mathrm{e}) \frac{e\phi}{k_B T} \tag{6.3.22} \end{align}\]のように展開できます。 これを(6.3.21)式の右辺に代入、さらに球対称を仮定すると
\[\begin{aligned} \frac{1}{r^2} \frac{d}{dr} \left( r^2 \frac{d\phi}{dr} \right) &= \frac{1}{r^2} \frac{d}{dr} \left( r \cdot r \frac{d\phi}{dr} \right) = \frac{1}{r^2} \frac{d}{dr} \left\{ r \left( \frac{d}{dr} (r\phi) - \phi \right) \right\} \\ &= \frac{1}{r^2} \left\{ \frac{d}{dr} (r\phi) - \phi + r \frac{d^2}{dr^2} (r\phi) - r \frac{d\phi}{dr} \right\} = \frac{1}{r} \frac{d^2}{dr^2} (r\phi) \end{aligned}\]のように変形できるため
\[\frac{d^2}{dr^2} (r\phi) = \frac{4\pi (N_\mathrm{i} Z_\mathrm{i}^2 + N_\mathrm{e}) e^2}{k_B T} r \phi = \frac{r\phi}{r_\mathrm{D}^2} \tag{6.3.23}\]ここで\(r_\mathrm{D}\)は
\[r_\mathrm{D} \equiv \sqrt{\frac{k_B T}{4\pi (N_\mathrm{i}Z_\mathrm{i}^2 + N_\mathrm{e}) e^2}} \simeq 0.9 \times 10^{-8} \sqrt{\frac{T_6 \mu_\mathrm{I}}{Z_\mathrm{i}(Z_\mathrm{i}+1) \rho}} \ [\mathrm{cm}] \tag{6.3.24}\]で定義される長さの次元を持つ量で、デバイ長と呼ばれます。 ここで\(T_6 \equiv T / 10^6 \mathrm{K}\)です。 (6.3.23)式の一般解は
\[r\phi = A e^{-r / r_\mathrm{D}} + B e^{r/r_\mathrm{D}}\]のように書かれますが、\(r \rightarrow \infty\)でゼロに減衰するためには、\(B = 0\)でなければなりません。 そして\(r \ll r_\mathrm{D}\)において電荷\(Z_\mathrm{i}e\)の原子核が作る静電ポテンシャルになるためには、\(A = Z_\mathrm{i} e\)とわかります。 よって
\[\phi = \frac{Z_\mathrm{i} e}{r} e^{-r / r_\mathrm{D}} \tag{6.3.25}\]が得られます。 \(r > r_\mathrm{D}\)では正の電荷\(Z_\mathrm{i} e\)が、電子によって強く遮蔽されていることがわかります。
原子核\(a, b\)が相対運動の運動エネルギー\(\mathcal{E}\)で近づくとき、クーロン障壁による古典的な折り返し地点の距離\(r_t\)は
となるため、デバイ長との比をとると
\[\frac{r_\mathrm{D}}{r_t} \simeq 62 \frac{\mathcal{E} \ [\mathrm{keV}]}{Z_a Z_b} \sqrt{\frac{T_6 \mu_\mathrm{I}}{Z_\mathrm{i} (Z_\mathrm{i} + 1) \rho}} \tag{6.3.27}\]のように書けます。 太陽の中心部では\(T_6 \sim 10, \rho \sim 10^2 \mathrm{g/ cm^3}\)です。 \(\mathcal{E}\)としてガモフピークの値\(\mathcal{E}_0 \sim 10 \mathrm{keV}\)を上式に代入すると、\(r_\mathrm{D} \gg r_t\)となっていることがわかります。 これは、太陽中心部で起こる核融合反応には、非常に弱い遮蔽効果が働くことを示しています。 このような弱い遮蔽の場合、原子核\(a, b\)間の静電エネルギーは
\[\frac{Z_a Z_b e^2}{r} e^{-r/r_\mathrm{D}} \approx \frac{Z_a Z_b e^2}{r} - \frac{Z_a Z_b e^2}{r_\mathrm{D}}\]のように表せます。 右辺第二項は場所に依存しない量であり、これは静電エネルギーを下げていることがわかります。 逆に相対運動のエネルギーが
\[\mathcal{E} \ \longrightarrow \ \mathcal{E} + U_0, \quad \left( U_0 \equiv \frac{Z_a Z_b e^2}{r_\mathrm{D}} \ll \mathcal{E}_0, \ \because r_\mathrm{D} \gg r_t (\mathcal{E}_0)\right) \tag{6.3.28}\]のように下駄をはかされたと考えても差し支えないでしょう。 遮蔽効果を考慮した量には添字\(\mathcal{s}\)、考慮していないものには\(\mathcal{ns}\)を付けて表すことにします。 すると反応断面積の平均値は、(6.3.3)式より
\[\langle \sigma v \rangle_\mathrm{s} = \int_0^\infty \sigma_\mathrm{ns} (\mathcal{E} + U_0) v(\mathcal{E}) f(\mathcal{E}) d\mathcal{E} = \int_{U_0}^\infty \sigma_\mathrm{ns} (\mathcal{E}') v(\mathcal{E}' - U_0) f(\mathcal{E}' - U_0) d\mathcal{E}' \tag{6.3.29}\]のように書けます。 (6.3.4)式から、\(f(\mathcal{E}) \propto \mathcal{E}^{1/2} e^{-\frac{\mathcal{E}}{k_B T}}\)と\(v(\mathcal{E}) \propto \mathcal{E}^{1/2}\)であることから
\[v(\mathcal{E}' - U_0) f(\mathcal{E}' - U_0) \propto v(\mathcal{E}' - U_0) \sqrt{\mathcal{E}'-U_0} e^{-\frac{\mathcal{E}'}{k_B T}} e^{\frac{U_0}{k_B T}} \propto v(\mathcal{E}') f(\mathcal{E}') e^{\frac{U_0}{k_B T}} \tag{6.3.30}\]のように書けます。 ここで\(\mathcal{E} \sim \mathcal{E}_0 \gg U_0\)を用いました。 (6.3.30)式を(6.3.29)に用い、積分の下限\(U_0\)を0とみなすと
\[\langle \sigma v \rangle_\mathrm{s} \simeq \langle \sigma v \rangle_\mathrm{ns} e^{\frac{U_0}{k_B T}} \tag{6.3.31}\]が得られます。 このように弱い遮蔽効果を考慮するには、反応率に\(e^{\frac{U_0}{k_B T}} \ (>1)\)をかければよいとわかります。 この因子を電子遮蔽因子 (screening factor)と呼びます。
水素燃焼
ppチェイン反応
4個の水素原子核(陽子)からヘリウム原子核が合成される核融合反応は、太陽のような主系列星のエネルギー源となっています。 水素原子核4個の質量は原子質量単位で\(4\times 1.0078=4.0312\)であるのに対し、ヘリウム原子核 (\(\alpha\)核)の質量は\(4.0026\)です。 この差は、ヘリウム原子核内の核子が結合エネルギー分だけ低いエネルギーを持っていることに対応します。 そしてヘリウム原子核生成の際に、この質量差に相当するエネルギーが放出されます。 すなわち、水素燃焼により質量の約0.7%がエネルギーに変えられることになります。 したがって、1gの水素がヘリウムとなった際に放出されるエネルギーは約\(6 \times 10^{18}\)ergです。
水素燃焼には、太陽質量程度以下の主系列星で主に起こるpp-chains (Proton-Proton chains)反応と、主に中大質量の主系列星で起こるCNO-cycles (Carbon-Nitrogen-Oxygen cycles)反応とがあります。
pp-chain反応では、クーロン反発力が比較的小さな(電荷の比較的小さな)原子核どうしの反応が起こります。 したがって、比較的温度の低い(\(T \lesssim 1.5 \times 10^7 \mathrm{K}\))領域で起こり、小質量 (\(M \lesssim 1.1 M_\odot\))の主系列星の中での主要な反応となります。
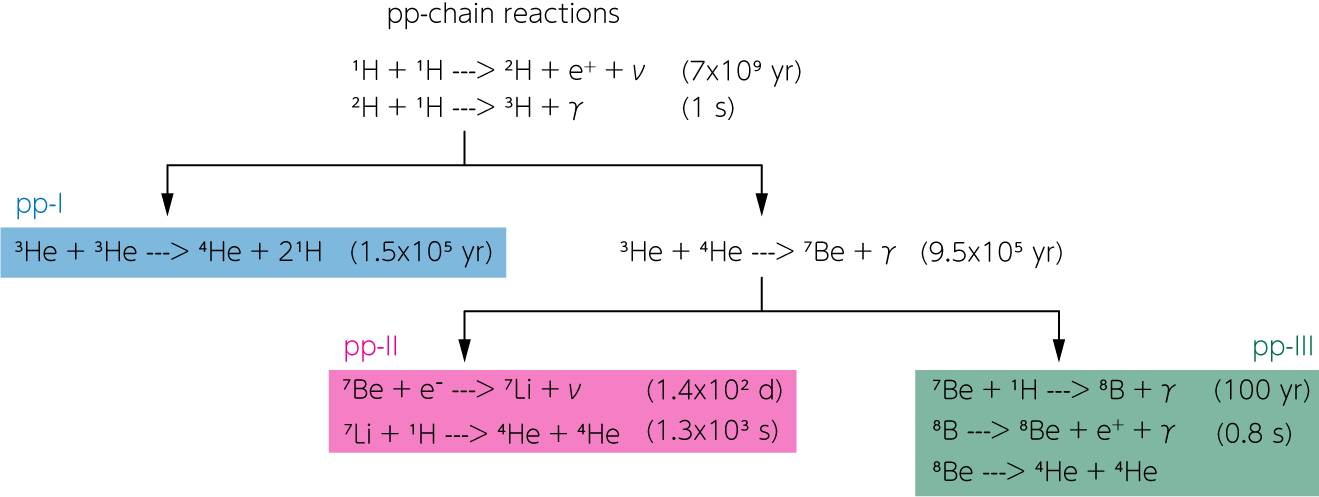
pp-chain反応にはpp-I, pp-II, pp-IIIの3つのchain反応があり、そのどのchainも陽子・陽子反応
\[{}^1 \mathrm{H} + {}^1 \mathrm{H} \rightarrow {}^2 \mathrm{H} + \mathrm{e}^+ + \nu_\mathrm{e} \tag{6.3.32}\]から始まります。 この反応は2つの陽子が遭遇した瞬間に、そのうちの1つの陽子が陽電子崩壊を起こし、重水素なることで完遂されます。 これらがほぼ同時に起こる必要があるため、非常に稀にしか起こらない反応です。 その単位体積あたりの反応率\(r_\mathrm{pp}\)は、近似的に
\[r_\mathrm{pp} \simeq 1.15 \times 10^9 X^2 \rho^2 T_9^{-2/3} e^{-3.380 / T_9^{1/3}} \ [\mathrm{cm^{-3} s^{-1}}] \tag{6.3.33}\]のように表されます。 ここで\(X\)は水素の質量含有量、\(T_9 \equiv T / 10^9 \mathrm{K}\)です。 この反応による陽子の平均寿命\(\tau_\mathrm{p}\)を求めてみましょう。
\[\frac{dN_\mathrm{H}}{dt} = -2 r_\mathrm{pp} \quad (N_\mathrm{H} = X \rho N_\mathrm{A})\]右辺の2は、1回の反応で2個の水素原子核が壊されることからきています。 ここで\(N_\mathrm{A}\sim 6.02 \times 10^{23}\)はアボガドロ数です。 これより
\[\tau_\mathrm{p} = \frac{N_\mathrm{H}}{\left\vert \frac{dN_\mathrm{H}}{dt} \right\vert} = \frac{X \rho N_\mathrm{A}}{2 r_\mathrm{pp}} \tag{6.3.34}\]と表されます。 \(T_6 \sim 15, \rho \sim 100 \ \mathrm{g/cm^3}, X=0.7\)に対して、\(\tau_\mathrm{p}\sim 6 \times 10^9 \ \mathrm{yr}\)となります。 pp-chain反応の中ではこの陽子・陽子反応が最も遅い反応なため、pp-chain反応の速さは陽子・陽子反応率により決まります。
陽子・陽子反応で生成された重水素は、すぐに陽子と反応して\({}^3 \mathrm{He}\)が生成されます。 その後に\({}^3 \mathrm{He}\)の起こす反応には、2種類があります。 その1つは、2つの\({}^3 \mathrm{He}\)が融合して1つのヘリウム原子核 (\({}^4 \mathrm{He}\), \(\alpha\)粒子)が生成され、2つの陽子が発生する反応です。 この一連の反応でヘリウムが生成される連鎖反応を、pp-I chainと呼びます。
\({}^3 \mathrm{He}\)が起こすもう一つの反応は、既存のヘリウム核 (\({}^4 \mathrm{He}\))と融合し、\({}^7 \mathrm{Be}\)を生成する反応です。 その次に\({}^7 \mathrm{Be}\)が起こす反応は、電子を捕獲するか陽子を捕獲するかにより2つに分かれます。 電子を捕獲する場合、\({}^7 \mathrm{Li}\)が生成され、その後\({}^7\mathrm{Li}\)が陽子を捕獲することで2つのヘリウムが生成されます。 この一連の反応をpp-II chain反応と呼ばれます。 一方で\({}^7 \mathrm{Be}\)が陽子を捕獲する場合は、\({}^8 \mathrm{B}\)ができます。 \({}^8 \mathrm{B}\)は半減期0.5秒で陽電子崩壊し、\({}^8 \mathrm{Be}\)を経てヘリウムが生成されます。 このとき放出されるニュートリノは高いエネルギーを持ち、太陽ニュートリノ観測に重要です。 \({}^8 \mathrm{Be}\)は非常に不安定な原子核です。 その平均寿命は約\(10^{-16}\)秒で、2つのヘリウム原子核に崩壊します。 この一連の反応がpp-III chainです。 pp-I, pp-II, pp-IIIの順に起こりにくい反応ですが、温度が高いほどpp-II, pp-IIIが起こりやすくなっています。
先程述べたように、pp-chain反応の完結する速さは、最初に起こる陽子・陽子反応率で決まっています。 そのため、どのchainを通ってもヘリウムができる速さは同じですが、各chainでニュートリノが持ち逃げするエネルギーは異なります。 よってQ-valueは各chainで少しづつ異なります。 各chainを通る割合は温度によって異なるため、effective Q-value \(Q(\mathrm{pp})_\mathrm{eff}\)は温度によって異なります。 これは近似的に
のように表すことができます。 (6.3.35)式と\(r_\mathrm{pp}\)を用いると、pp-chainsによるエネルギー発生率を近似的に
\[\epsilon (\mathrm{pp}) = \frac{r_\mathrm{pp} Q_\mathrm{eff}}{\rho} \simeq 2.4 \times 10^4 \frac{\rho X^2}{T_9^{2/3}} e^{-3.380 / T_9^{1/3}} \ [\mathrm{erg/g/s}] \tag{6.3.36}\]のように表されます。 このエネルギー発生率の温度依存性は
\[\begin{align} \frac{\partial \ln \epsilon (\mathrm{pp})}{\partial \ln T} &= \frac{\partial}{\partial \ln T} (\ln T_9^{-2/3} + \ln e^{-3.38 T_9^{-1/3}}) = -\frac{2}{3} -3.38 \frac{\partial}{\partial \ln T} T_9^{-1/3} \notag \\ &= -\frac{2}{3} -3.38 \frac{\partial}{\partial \ln T} \left( \frac{T_6}{10^3}\right)^{-1/3} = -\frac{2}{3} + \frac{33.8}{3} T_6 T_6^{-4/3} \notag \\ &= -\frac{2}{3} + \frac{11.3}{T_6^{1/3}} \tag{6.3.37} \end{align}\]CNOサイクル
CNOサイクルは、陽子が炭素・窒素・酸素の原子核内に次々に捕獲され、4個の水素が捕獲された時に1つのヘリウム原子核が生成され、さらに重元素原子核は元に戻るというサイクルです。 すなわち、CNOの原子核は触媒の働きをし、CNO全体の含有量は変化しません。 ただしCNOの個々の元素の含有量は変化します。
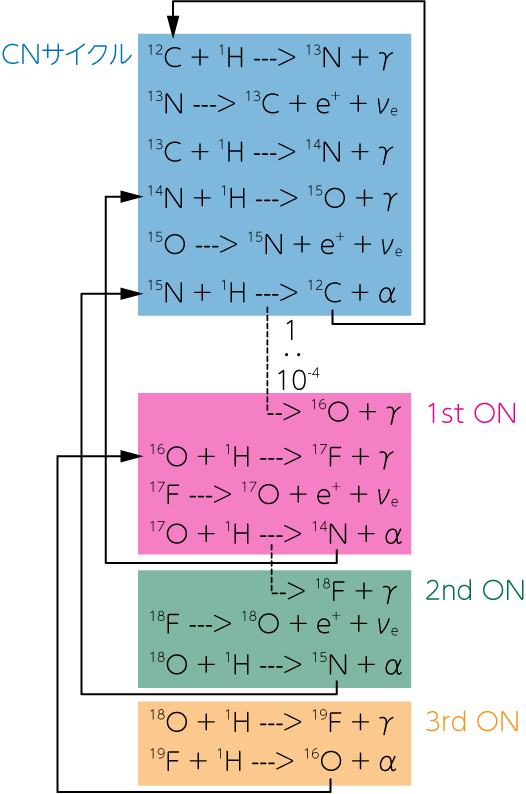
(どの反応から開始しても良いですが)例えば\({}^{12} \mathrm{C} (\mathrm{p}, \gamma) {}^{13} \mathrm{N}\)のあと、\({}^{13}\mathrm{N}\)が陽電子崩壊してできた\({}^{13} \mathrm{C}\)がさらに陽子を捕獲します。 これを繰り返し、\({}^{15} \mathrm{N}\)が4つ目の陽子を捕獲することで、\({}^{15} \mathrm{N} (\mathrm{p}, \alpha) {}^{12} \mathrm{C}\)が発生します。 この最後の反応により、1つのヘリウム原子核ともとの\({}^{12} \mathrm{C}\)ができ、サイクルが閉じます。 このサイクルは、特にCNサイクルと呼ばれることもあります。 \({}^{15} \mathrm{N}\)の陽子捕獲反応では、\({}^{15} \mathrm{N} (\mathrm{p}, \alpha) {}^{12} \mathrm{C}\)の他に、これに対して\(10^{-4}\)の頻度で\({}^{15} \mathrm{N} (\mathrm{p}, \gamma) {}^{16} \mathrm{O}\)の反応も起こります。 この反応により、\({}^{16} \mathrm{O}, {}^{17} \mathrm{O}\)を介してもう一度\({}^{14} \mathrm{N}\)に戻る、もう一つのサイクルができます。
CNOサイクル中の反応では、\({}^{14} \mathrm{N} (\mathrm{p}, \gamma) {}^{15} \mathrm{O}\)の反応が最も遅いことが知られています。 そのため、この反応率がCNOサイクルの循環の速さを決定します。 よってこのサイクルが平衡状態になった段階では、最初に存在したCNO元素のほぼ全てが\({}^{14}\mathrm{N}\)になります。
私たちの周りにある窒素のほとんどが、CNOサイクルによって作られたと考えられています。
またCNOサイクルに起因する元素蘇生に関するもう一つ顕著な特徴は、\({}^{12}\mathrm{C}/{}^{13}\mathrm{C}\)の比に現れます。 Cosmic abundanceにおけるこの比は100近い値となるが、CNOサイクルの平衡状態では、この値は4程度まで下がります。 この同位体元素比の大きな変化は、CNOサイクル内での反応\({}^{12} \mathrm{C} (\mathrm{p}, \gamma) {}^{13} \mathrm{N}, {}^{13} \mathrm{C} (\mathrm{p}, \gamma) {}^{14} \mathrm{N}\)の反応率\(\langle \sigma v \rangle\)の違いはほとんど質量の違いだけから生じるもので、その差が4倍程度にしかならないためです。 実際、赤色巨星で\({}^{14} \mathrm{N} / {}^{12} \mathrm{C}, {}^{12} \mathrm{N} / {}^{13} \mathrm{C}\)等の値が、主系列星とは著しく異なる値の観測結果が示されています。 これらは赤色巨星の対流外層が恒星内部深くまで侵入し、CNOサイクルが起こっていた場所の物質を対流層に取り込んだことを示しています。
CNOサイクルの回る速さが\({}^{14} \mathrm{N} (\mathrm{p}, \gamma) {}^{15} \mathrm{O}\)の反応率で決まっていることと、初期にあったCNO元素のほぼ全てが\({}^{14} \mathrm{N}\)になることから、CNOサイクルのエネルギー発生率は近似的に
のように書かれます。 ここでCNO元素の含有量は、重元素全体の含有量\(Z\)の半分であるという近似を用いました。 上述のCNOサイクルのエネルギー発生率から、その温度依存性は
\[\begin{align} \frac{\partial \ln \epsilon (\mathrm{CNO})}{\partial \ln T} &\simeq \frac{\partial}{\partial \ln T} (\ln T_9^{-2/3} + \ln e^{-15.228/T_9^{1/3}}) = -\frac{2}{3} - 15.228 \frac{\partial}{\partial \ln T} T_9^{-1/3} \notag \\ &= -\frac{2}{3} - 15.228 \frac{\partial}{\partial \ln T} \left( \frac{T_6}{10^3}\right)^{-1/3} = -\frac{2}{3} + \frac{152.28}{3} T_6 T_6^{-4/3} \notag \\ &= -\frac{2}{3} + \frac{50.8}{T_6^{1/3}} \tag{6.3.39} \end{align}\]のように表されます。 この値は、\(T_6 = 20\)で20となります。 これは先ほどのpp-chainsの場合よりも、大きい値です。 CNOサイクル中の反応は、pp-chainsの場合に比べ大きな電荷をもつ原子核が関与しているため、クーロン障壁の高さに起因します。
CNOサイクルはpp-chain反応よりも高温で発生し、\(M \gtrsim 1.2 M_\odot\)の主系列星の中で優勢となります。
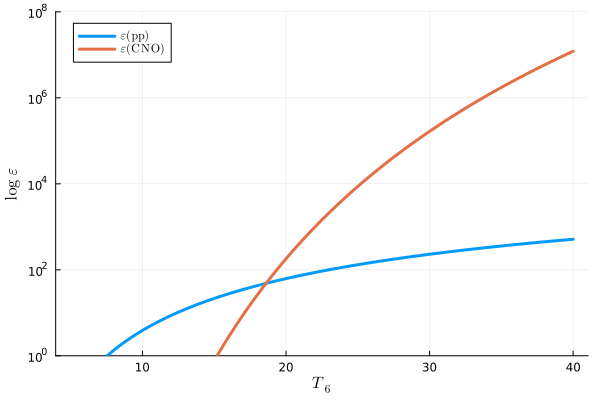
上図は\(\rho = 100 \mathrm{g/cm^3}, X=0.7, Z=0.01\)とした場合の、(6.3.36)式と(6.3.38)式を描画したものです。 この図からわかるように、CNOサイクルは2000万K以上になるとppチェインよりも効率的にエネルギーを放出するようになります。
ヘリウム燃焼
温度が\(10^8\)K程度になると、3個のヘリウム原子核が炭素原子核に融合する反応が起きます。 この核融合は、次の二段階の反応で起こります。
\[{}^4 \mathrm{He} + {}^4 \mathrm{He} \longleftrightarrow {}^8 \mathrm{Be}, \quad {}^8 \mathrm{Be} + {}^4 \mathrm{He} \longrightarrow {}^{12} \mathrm{C} + \gamma \tag{6.3.40}\]\({}^8 \mathrm{Be}\)は不安定な原子核で、\(10^{-16}\)sの寿命で2つの\({}^4 \mathrm{He}\)に崩壊します。 そのため\({}^4 \mathrm{He}\)と\({}^8 \mathrm{Be}\)の間の反応は平衡状態にあり、\(T=10^8\mathrm{K}, \rho=10^5 \mathrm{g/cm^3}\)では、\(10^9\)個の\({}^4 \mathrm{He}\)に対して1個の割合で\({}^8 \mathrm{Be}\)が存在します。 そのわずかな量の\({}^8 \mathrm{Be}\)にさらに\({}^4 \mathrm{He}\)が反応し、\({}^{12} \mathrm{C}\)が生成されます。 この一連の反応は、トリプル-アルファ反応と呼ばれています。 1gの\({}^4 \mathrm{He}\)が\({}^{12} \mathrm{C}\)に融合する際に発生するエネルギーは\(6\times 10^{17}\)ergで、水素燃焼の約1/10です。 そのエネルギー発生率は近似的に
\[\epsilon (3\alpha) = \frac{N_\alpha^3}{3! \rho} \langle \sigma v \rangle_{3\alpha} Q_{3\alpha} \simeq 5.1 \times 10^8 \rho^2 Y^3 \frac{e^{-4.4027 / T_9}}{T_9^3} \ [\mathrm{erg/g/s}] \tag{6.3.41}\]と表されます。 ここで\(N_\alpha^3 / 3!\)は、\(N_\alpha \ (\gg 1)\)から3個のヘリウム原子核を取り出す場合の数 \({}_{N_\alpha} C_3\)からくるものです。 また\(Q_{3\alpha} = 7.275 \mathrm{MeV}\)であり、\(T_9 \equiv T / (10^9 \mathrm{K})\)です。
トリプル-アルファ反応と同時に
の反応も起こります。 これらの反応に対する単位質量あたりのエネルギー発生率は
\[\epsilon (\alpha, {}^{12} \mathrm{C}) = \frac{N_\alpha N_{12}}{\rho} \langle \alpha 12 \rangle Q_{\alpha 12} \simeq 10^{25} \frac{YX_{12} \rho}{T_9^2} \exp \left\{ -\frac{32.12}{T_9^{1/3}} - (0.286T_9)^2\right\} \ [\mathrm{erg / g/ s}] \tag{6.3.42}\] \[\epsilon (\alpha, {}^{16} \mathrm{O}) = \frac{N_\alpha N_{16}}{\rho} \langle \alpha 16 \rangle Q_{\alpha 16} \simeq 6.7 \times 10^{26} \frac{YX_{16} \rho}{T_9^{2/3}} \exp \left\{ -\frac{39.757}{T_9^{1/3}} - (0.631T_9)^2\right\} \ [\mathrm{erg / g/ s}] \tag{6.3.43}\]のように表されます。 ここで\(N_{12}, X_{12}\)はそれぞれ\({}^{12} \mathrm{C}\)の数密度と質量含有比 (単位質量あたりに含まれる\({}^{12} \mathrm{C}\)の質量)、そして\(N_{16}, X_{16}\)はそれぞれ\({}^{16} \mathrm{O}\)の数密度と質量含有比を表します。 またそれぞれの反応の\(\langle \sigma v\rangle\)を、\(\langle \alpha 12\rangle, \langle \alpha 16\rangle\)のように書きました。
ヘリウム燃焼後に残るのは、炭素と酸素(そしてわずかなネオン・マグネシウム: 上述の反応で生成されたネオンがさらに\(\alpha\)核を捕獲してMgとなる)の金剛ガスです。 燃焼時の温度が高いほど (つまり質量の大きい恒星の場合ほど)酸素の割合が多くなります。 しかし\({}^{12} \mathrm{C} (\alpha, \gamma) {}^{16} \mathrm{O}\)反応の反応断面積は、まだ2倍程度不確定です。 そのためヘリウム燃焼が終わった時に残される炭素・酸素の比の絶対値を、よく決定することはできません。
ヘリウム燃焼の点火時に、電子の縮退圧で中心核が支えられているような小質量星 (\(M \lesssim 2M_\odot\))の場合、圧力の温度依存性が小さいために、ヘリウム燃焼の点火に際しフラッシュと呼ばれる熱的暴走が起こり、構造の変化が急激に起こります。 一方、中・大質量性の場合は、ヘリウム燃焼段階への構造の変化には劇的な現象は伴いません。
炭素、ネオン、酸素燃焼など
ヘリウム燃焼後は、炭素・ネオン・酸素・シリコンなどの燃焼が起こります。 これらの融合反応は高温で起こるため、ニュートリノによるエネルギー損失も重要となります。 融合反応によるエネルギー発生率が、ニュートリノエネルギー損失率によりも大きくなったとき、重力収縮を止めることができます。 そのため、その時点で各燃焼段階が始まる(ignition)と言えます。
炭素燃焼
\(T_9 \sim 0.5 - 1\)の高温になると、炭素燃焼が起こります。 炭素燃焼では
\[{}^{12} \mathrm{C} + {}^{12} \mathrm{C} \ \longrightarrow \ \left\{ \begin{array}{cc} {}^{20} \mathrm{Ne} + \alpha & (44\%) \\ {}^{23} \mathrm{Na} + p & (56\%) \end{array} \right.\]の反応が起こります。 生成された陽子は
\[{}^{23} \mathrm{Na} + p \ \longrightarrow \ {}^{20} \mathrm{Ne} + \alpha, \quad {}^{23} \mathrm{Na} + p \ \longrightarrow \ {}^{24} \mathrm{Mg} + \gamma\]の反応に用いられます。 またヘリウムは\({}^{16} \mathrm{O} (\alpha, \gamma) {}^{20} \mathrm{Ne}, {}^{20} \mathrm{Ne} (\alpha, \gamma) {}^{24} \mathrm{Mg}\)などの反応を起こします。 さらに温度が高い場合、\({}^{24} \mathrm{Mg} (\alpha, \gamma) {}^{28} \mathrm{Si}\)という反応も起こります。 したがって、炭素燃焼が終わったときに残る元素は、\({}^{16} \mathrm{O}, {}^{20} \mathrm{Ne}, {}^{24} \mathrm{Mg}\)、そして少量の\({}^{28} \mathrm{Si}\)となります。 1グラムの\({}^{12} \mathrm{C}\)が\({}^{20} \mathrm{Ne}, {}^{24} \mathrm{Mg}\)に変えられるときに放出されるエネルギーは、およそ\(4\times 10^{17} \mathrm{erg/g}\)です。
ネオン燃焼
\(T_9 > 1.5\)では、エネルギーの高い光子がネオン原子核を壊す反応
\[{}^{20} \mathrm{Ne} + \gamma \ \longrightarrow \ {}^{16} \mathrm{O} + \alpha, \quad Q = -4.73 \mathrm{Mev}\]が、その逆反応より速く起こるようになります。 生成されたヘリウムは、\({}^{20} \mathrm{Ne} (\alpha, \gamma) {}^{24} \mathrm{Mg}\)という反応に用いられます。 これらの反応を合わせると
\[2 {}^{20} \mathrm{Ne} + \gamma \ \longrightarrow \ {}^{16} \mathrm{O} + {}^{24} \mathrm{Mg} + \gamma, \quad Q = + 4.583 \mathrm{MeV}\]のように、\({}^{20} \mathrm{Ne}\)が\({}^{16} \mathrm{O}, {}^{24} \mathrm{Mg}\)となってエネルギーを発生するネオン燃焼となります。 この燃焼で放出されるエネルギーは、1グラムの\({}^{20} \mathrm{Ne}\)あたり、\(1.1 \times 10^{17} \mathrm{erg/g}\)です。
酸素燃焼
\(T_9 \sim 2\)では、酸素燃焼が起こります。 そこでは
\[{}^{16} \mathrm{O} + {}^{16} \mathrm{O} \ \longrightarrow \ \left\{ \begin{array}{cc} {}^{31} \mathrm{P} + p + 7.68 \mathrm{MeV} & (56\%) \\ {}^{28} \mathrm{Si} + \alpha + 9.59 \mathrm{MeV} & (34\%) \\ {}^{31} \mathrm{S} + n + 1.45 \mathrm{MeV} & (5\%) \\ {}^{30} \mathrm{P} + d - 2.41 \mathrm{MeV} & (5\%) \\ \end{array} \right.\]などの反応が起こります。 それらの生成物により、種々の反応が起きます (ただし比較的低温では重水素の生成される吸熱反応は起こりません。) 最終的には、多量の\({}^{28} \mathrm{Si}\)と\({}^{32} \mathrm{S}, {}^{40} \mathrm{Ca}\)などの重元素が残ります。 酸素燃焼により1グラムの\({}^{16} \mathrm{O}\)から放出されるエネルギーは、およそ\(5 \times 10^{17} \mathrm{erg/g}\)です。
シリコン燃焼
\(T_9 >3\)になると、\({}^{28} \mathrm{Si}\)が光子に破壊され、\(n, p, \alpha\)粒子を放出します。 そしてそれらから、非常に多くの種類の核反応が起こり始めます。 そこでは、結合エネルギーの低い原子核ほど多く存在するような、統計的平衡に近い状態となります。 そして最も安定な原子核である、\({}^{56} \mathrm{Fe}\)が最も多くできます。 1グラムの\({}^{28} \mathrm{Si}\)が\({}^{56} \mathrm{Ni}\)に変わるときに放出されるエネルギーは、およそ\(2 \times 10^{17} \mathrm{erg/g}\)です。
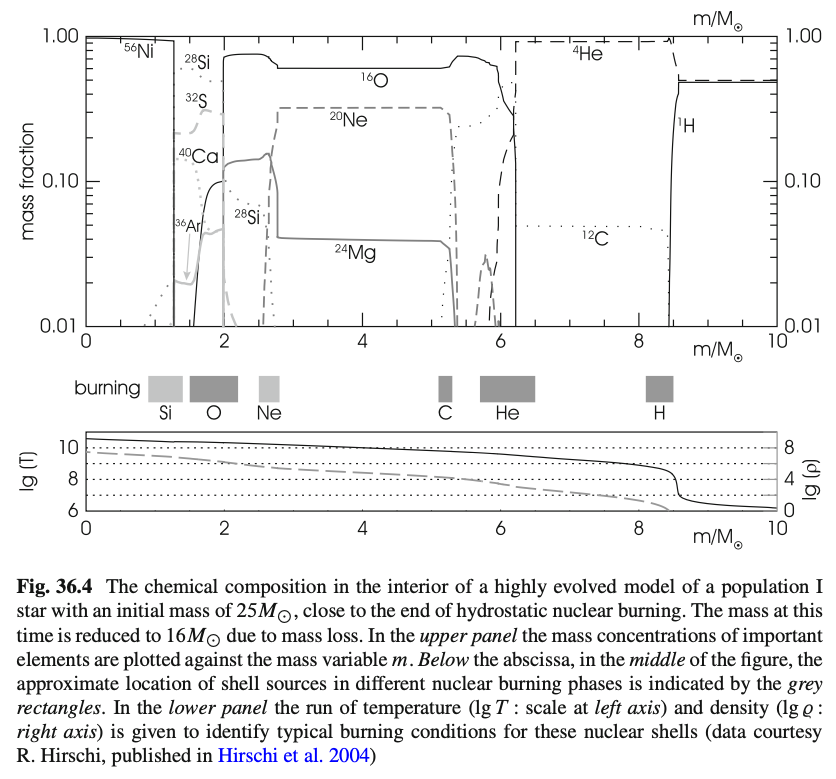
次の図は、最終段階まで進化した大質量星 (\(25 M_\odot\))内部の元素組成の分布を計算したものです。 横軸は半径の代わりに質量\(m / M_\odot\)を取っています。 中心(図の左側)ではシリコン燃焼がすでに終わり、鉄グループの元素\({}^{56}\mathrm{Ni}\)によって構成される中心核が形成されます。 図の下の灰色で記された部分は、各燃焼の起こっている球殻 (shell)の位置を表しています。 この図から、中心部から外側に向かって重い原子核から軽い原子核の層が次々と重なるような構造がわかります。 これをタマネギ構造と呼ばれます。
参考文献
[1] Moscato & Grebogi, 2024, “Approximating the nuclear binding energy using analytic continued fractions”
[2] Boccioli & Roberti, 2024, “The Physics of Core-Collapse Supernovae: Explosion Mechanism and Explosive Nucleosynthesis”
[3] Kippenhahn, Weigert & Weiss, “Stellar Structure and Evolution”
[4] 高原文郎, “宇宙物理学”
[5] 野本憲一, 定金晃三, 佐藤勝彦, “恒星”