磁気流体方程式の運動量保存則

流体要素の運動方程式の変形

磁気流体を構成する流体要素の運動方程式は

\[\rho \frac{D \mathbf{v}}{Dt} = - \nabla P + \mathbf{j} \times \frac{\mathbf{B}}{c} + \mathbf{F} \tag{1}\]

のように書かれます。ここで\(\rho, \mathbf{v}, P, \mathbf{j}, \mathbf{B}, \mathbf{F}\)はそれぞれ質量密度、流体要素の速度ベクトル、ガス圧、電流密度ベクトル、磁場ベクトル、外力ベクトルを表します。右辺第1項は圧力勾配による力、第2項はLorentz力により加速度がもたらされることを意味する式です。
左辺のLagrange微分をEuler微分に書き換えると

\[\rho \frac{D \mathbf{v}}{D t} = \rho \left\{ \frac{\partial \mathbf{v}}{\partial t} + (\mathbf{v} \cdot \nabla) \mathbf{v} \right\} = \frac{\partial}{\partial t} (\rho \mathbf{v}) - \mathbf{v} \frac{\partial \rho}{\partial t} + \rho \{ (\mathbf{v} \cdot \nabla) \mathbf{v} \}\]

ここで連続の式よりさらに式変形を行うと

\[\rho \frac{D \mathbf{v}}{D t} = \frac{\partial}{\partial t} (\rho \mathbf{v}) + \mathbf{v} \{ \nabla \cdot (\rho \mathbf{v})\} + \rho \{ (\mathbf{v} \cdot \nabla) \mathbf{v} \}\]

ここで第2, 3項の\(i\)成分のみを計算してみましょう。すると

\[v_i \partial_j (\rho v_j) + \rho (v_j \partial_j) v_i = \partial_j (\rho v_i v_j)\]

のように変形できます。ここで\(\partial_j = \frac{\partial}{\partial x_j}\)、さらに添字の和の記号を省略するEinstein縮約記法を用いました。すると(1)式は

\[\frac{\partial}{\partial t} (\rho \mathbf{v}) + \nabla \cdot (\rho \mathbf{v} \mathbf{v}) = - \nabla P + \mathbf{j} \times \frac{\mathbf{B}}{c} + \mathbf{F} \tag{2}\]

のようになります。ここで\(\nabla \cdot (\rho \mathbf{v} \mathbf{v}) = \frac{\partial}{\partial x_j}\rho \mathbf{v} v_j\)です。
続いて、右辺のLorentz力の項を変形しましょう。Maxwell方程式において変位電流を無視した\(\nabla \times \mathbf{B} = \frac{4\pi}{c} \mathbf{j}\)より

\[\begin{aligned} \mathbf{j} \times \frac{\mathbf{B}}{c} &= \frac{1}{4\pi} (\nabla \times \mathbf{B}) \times \mathbf{B} = \frac{1}{4\pi} \epsilon_{ijk} (\nabla \times \mathbf{B})_j B_k \mathbf{e}_i = \frac{1}{4\pi} \epsilon_{ijk} \epsilon_{j \ell m} (\partial_\ell B_m) B_k \mathbf{e}_i \\ &= \frac{1}{4\pi} \epsilon_{jki} \epsilon_{j \ell m} B_k (\partial_\ell B_m) \mathbf{e}_i = \frac{1}{4\pi} (\delta_{k\ell} \delta_{im} - \delta_{km} \delta_{i\ell}) B_k (\partial_\ell B_m) \mathbf{e}_i = \frac{1}{4\pi} \{ B_k (\partial_k B_i) - B_k (\partial_i B_k) \} \mathbf{e}_i \\ &= \frac{1}{4\pi} \left\{ (\mathbf{B} \cdot \nabla) B_i - \frac{1}{2} \partial_i B_k^2 \right\} \mathbf{e}_i = \frac{1}{4\pi} (\mathbf{B} \cdot \nabla) \mathbf{B} - \frac{1}{8\pi} \nabla B^2 \end{aligned}\]

以上より

\[\frac{\partial}{\partial t} (\rho \mathbf{v}) + \nabla \cdot (\rho \mathbf{v} \mathbf{v}) = - \nabla \left( P + \frac{B^2}{8\pi} \right) + \frac{1}{4\pi} (\mathbf{B} \cdot \nabla) \mathbf{B} + \mathbf{F} \tag{3}\]

となります。

Maxwell応力テンソルによる記述

さらにMaxwell応力テンソル

\[M_{ij} = \frac{1}{4\pi} B_i B_j - \frac{1}{8\pi} B^2 \delta_{ij} \tag{4}\]

を用いると

\[\begin{align} \partial_j M_{ij} &= \frac{1}{4\pi} \{ B_j (\partial_j B_i) + B_i (\partial_j B_j) \} - \frac{1}{8\pi} \partial_i B^2 \notag \\ &= \frac{1}{4\pi} \{ (\mathbf{B} \cdot \nabla) B_i + B_i \underbrace{(\nabla \cdot \mathbf{B})}_{=0} \} - \frac{1}{8\pi} ( \nabla B^2)_i = \frac{1}{4\pi} (\mathbf{B} \cdot \nabla) B_i - \frac{1}{8\pi} (\nabla B^2)_i \tag{5} \end{align}\]

(3), (5)式より

\[\frac{\partial}{\partial t} (\rho \mathbf{v}) + \nabla \cdot (\rho \mathbf{v} \mathbf{v}) = - \nabla P + \nabla \cdot \mathbf{M} + \mathbf{F}\]

と書けます。さらに運動量流束\(\rho \mathbf{v} \mathbf{v}\)と圧力勾配の部分もひとまとめにして

\[\pi_{ij} = \rho v_i v_j - \frac{1}{4\pi} B_i B_j + \left( P + \frac{B^2}{8\pi} \right) \delta_{ij} \tag{6}\]

のように書けば、運動量保存則を表す式の\(i\)成分は

\[\frac{\partial}{\partial t} (\rho v_i) + \partial_j \pi_{ij} = F_i \tag{7}\]

のように簡潔に表すことができます。

各項の意味

以下では\(\rho \mathbf{v} \mathbf{v}, \frac{1}{4\pi} (\mathbf{B} \cdot \nabla) \mathbf{B}, \frac{1}{8\pi} \nabla B^2\)の意味について考えましょう。

\(\rho \mathbf{v} \mathbf{v}\)の意味

(2)式に現れた\(\{ \nabla \cdot (\rho \mathbf{v} \mathbf{v}) \}_i = \partial_j (\rho v_i v_j)\)について考えましょう。磁場や外力がない場合を考えると

\[\frac{\partial}{\partial t} (\rho v_x) = - \nabla \cdot (\rho v_x \mathbf{v})\]

となります。ここで\(i=x\)の場合を考えました。さらにわかりやすくするために、これをある座標の体積\(V\)で体積積分しましょう。するとGaussの定理より

\[\frac{\partial }{\partial t} \iiint_V \rho v_x dV = - \iint_S \rho v_x \mathbf{v} \cdot d\mathbf{S}\]

と書けます。ここで\(S\)は体積\(V\)の表面領域を表します。すると右辺は表面\(S\)を通過して出入りする運動量\(\rho v_x\)の合計を表していることがわかります。よって\(\rho \mathbf{v} \mathbf{v}\)は運動量流束を表しています。
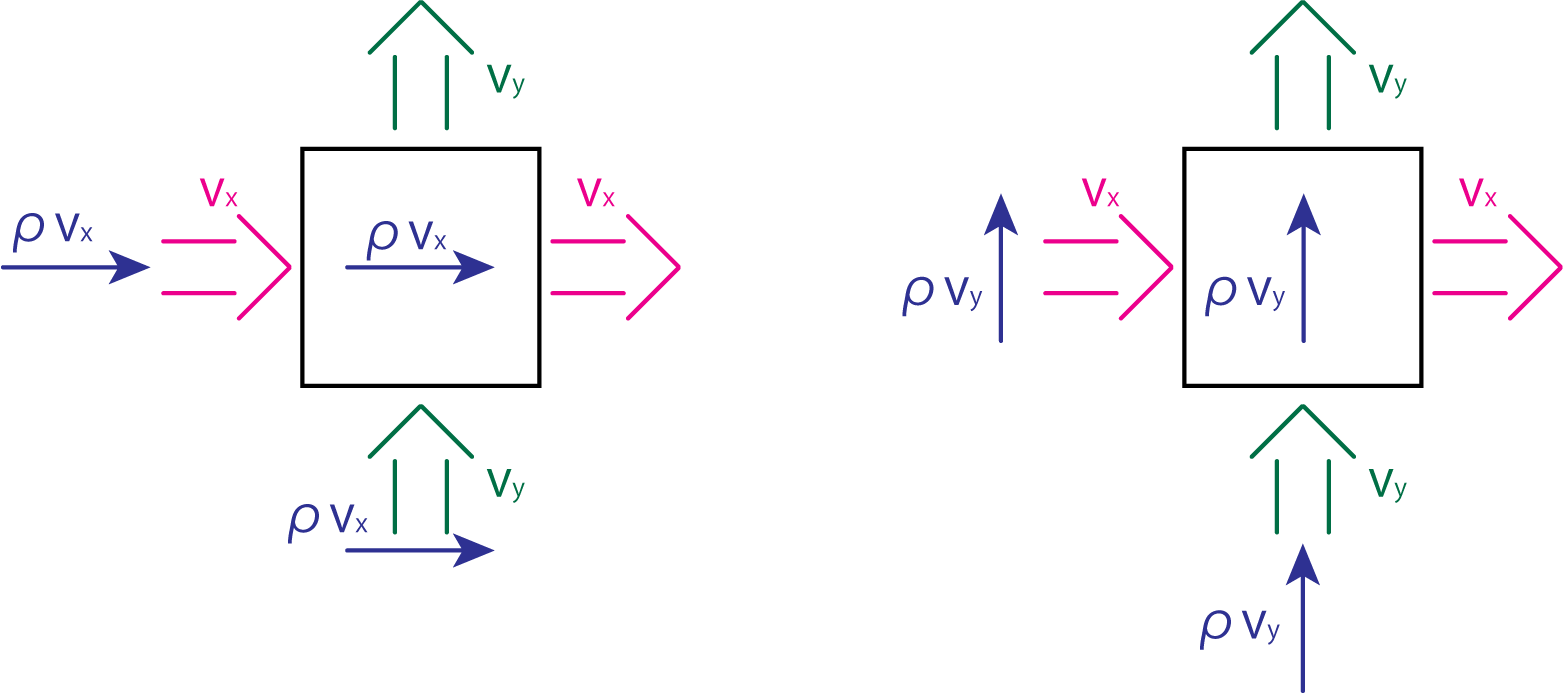
\(\rho v_x v_x\)は\(x\)方向の運動量\(\rho v_x\)が\(v_x\)によって単位時間に運ばれる量を表します。\(\rho v_x v_y\)は同様に\(\rho v_x\)が\(v_y\)によって単位時間に運ばれる量を表します。\(\rho v_y v_x\)は\(\rho v_y\)という\(y\)方向の運動量が\(v_x\)によって運ばれることを表しており、\(\rho v_x v_y\)と表記は同じですが意味が異なることに注意してください。

\(\frac{1}{4\pi} (\mathbf{B} \cdot \nabla) \mathbf{B}\)の意味

次に(3)式の\(\frac{1}{4\pi} (\mathbf{B} \cdot \nabla) \mathbf{B}\)について考えましょう。\(\mathbf{B} \cdot \nabla\)は磁場の方向(磁力線)に沿って微分するという演算子であることがわかります。よって\((\mathbf{B} \cdot \nabla) \mathbf{B}\)は、磁力線に沿って微小距離\(\Delta\)だけ離れた2つの場所での接ベクトル(すなわち磁場)差をとり、\(\Delta \rightarrow 0\)の極限を計算しなさいということがわかります。下図のように曲がった磁力線が存在しているとすると、この項は磁力線の曲がり具合を減らす方向を向いたベクトルとわかります。

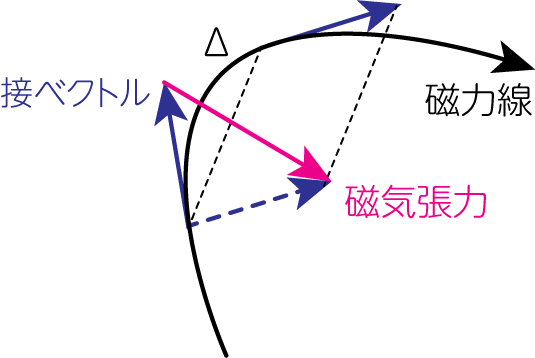
これはゴムひもの張力のような役割をしていることがわかるため、この類推からこれを磁気張力(magnetic tension)と呼びます。なお、磁力線が真っ直ぐの場合には、流体にはこの力は働かないことがわかります。

\(\frac{1}{8\pi} \nabla B^2\)の意味

(3)式において圧力と同じ働きをしていることから、この項は磁気圧力と呼ばれます。\(\frac{1}{8\pi} \nabla B^2\)は磁場のエネルギー密度と見ることもできるため、エネルギー等分配により磁場のエネルギーが局所的に高い部分から低い部分に輸送される様子を表すと見ることもできます。磁力線が混み合っている蜜の部分から疎の部分に向かう方向に力が働くと考えて良いでしょう。