Table of contents
熱制動吸収 (Thermal free-free absorption)
シンクロトロン自己吸収のときと同様に、熱制動放射を出す天体についても、逆過程となる吸収が存在します。 今回は熱制動放射で輝いて見える天体について、その吸収係数やこの吸収過程によるスペクトル変化を求めてみましょう。
吸収係数
吸収係数の定義、そして熱制動放射を求めるときに用いた熱平衡の仮定より
\[\eta_\nu = \alpha_\nu^{ff} B_\nu (T) \tag{1}\]左辺の\(\eta_\nu\)は発光係数、そして右辺の\(\alpha_\nu, B_\nu (T)\)はそれぞれ吸収係数とプランク関数です。 この関係式をキルヒホッフの関係式と呼びます。 \(B_\nu (T)\)は単位時間・単位面積・単位立体角あたりに通過する光のエネルギーです。 今、\(\eta_\nu\)を熱制動放射による発光と考えると
\[\eta_\nu = \frac{1}{4\pi} \epsilon_\nu^{ff} \tag{2}\]のように書けます。 ここで\(1/4\pi\)は単位立体角あたりの量に直すためのものです。 この2つの式より
\[\begin{align} \alpha_\nu^{ff} &= \frac{\epsilon_\nu^{ff}}{4\pi B_\nu(T)} = \frac{1}{4\pi} \frac{2^5\pi e^6}{3 m_e c^3} \sqrt{\frac{2\pi}{3m_e k_B}} n_e^2 T^{-1/2} \tilde{g}_{ff} e^{-h\nu / k_B T} \frac{c^2}{2h\nu^3} (e^{h\nu/k_B T} -1) \notag \\ &= \frac{4 e^6}{3 m_e hc} \sqrt{\frac{2\pi}{3m_e k_B}} \tilde{g}_{ff} n_e^2 T^{-1/2} \nu^{-3} (1-e^{-h\nu/k_B T}) \tag{3} \end{align}\]のように、吸収係数が求まります。 ではこの吸収が観測で効いてくるのは、どのような振動数\(\nu\)のときでしょうか。 (3)式から、\(h \nu \gg k_B T\)の高周波の場合には\(\nu^{-3} \ll 1, e^{-h\nu / k_B T} \ll 1\)より、\(\alpha_\nu^{ff} \ll 1\)となります。 よって高周波の観測では吸収は無視して良いでしょう。 逆に\(h \nu \ll k_B T\)の低周波領域の場合、すなわちレイリー・ジーンズ側においては
\[\begin{align} \alpha_\nu^{ff} &\simeq \frac{4 e^6}{3 m_e hc} \sqrt{\frac{2\pi}{3m_e k_B}} \tilde{g}_{ff} n_e^2 T^{-1/2} \nu^{-3} \left\{ 1- \left( 1- \frac{h\nu}{k_B T} \right) \right\} \notag \\ &\simeq \frac{4 e^6}{3 m_e c k_B} \sqrt{\frac{2\pi}{3m_e k_B}} \tilde{g}_{ff} n_e^2 T^{-3/2} \nu^{-2} \notag \\ &\simeq \left( \frac{e^3}{\hbar c} \right)^3 (\hbar c)^3 \frac{c^2}{(m_e c^2)^{3/2}} \frac{1}{c} \frac{10^6}{(k_B 10^4)^{3/2}} \frac{2^{5/2} \pi^{1/2}}{3^{3/2}} \tilde{g}_{ff} n_e^2 T^{-3/2} \nu^{-2} \notag \\ &\simeq \left( \frac{200 \mathrm{MeV \cdot fm}}{140} \right)^3 \frac{(3 \times 10^{10})^2}{(0.5 \mathrm{MeV})^{3/2}} \frac{10^6}{(10^{-6} \mathrm{MeV})^{3/2}} \frac{2^{5/2} \pi^{1/2}}{3^{3/2}} \tilde{g}_{ff} n_e^2 T^{-3/2} \nu^{-2} \notag \\ &\simeq \left( \frac{10^{-12}}{7} \right)^3 (3 \times 10^{10})^2 2^{3/2} \times 10^6 \times 10^9 \frac{2^{5/2} \pi^{1/2}}{3^{3/2}} \tilde{g}_{ff} n_e^2 T^{-3/2} \nu^{-2} \notag \\ &\simeq 0.014 \tilde{g}_{ff} n_e^2 T^{-3/2} \nu^{-2} \tag{4} \end{align}\]のように求まります。
もう少ししっかり計算を行うと、前の係数はおよそ0.018程度になります。
吸収によるスペクトルの変化
ここまでの議論から、吸収が低周波側で効くことがわかりました。 ではその低周波側において、熱制動放射のスペクトルはどのように変化するのでしょうか。 それを求めるには輻射輸送の方程式の形式的な解を用います。
\[I_\nu = S_\nu (1 - e^{-\tau_\nu}) \tag{5}\]ここで\(S_\nu\)は源泉関数、そして\(\tau_\nu\)は光学的厚みです。 (5)式は、もともと\(S_\nu\)の光の強さで発光が起こりましたが、光線が光学的厚み\(\tau_\nu\)の媒質中を伝播することで\(e^{-\tau_\nu} S_\nu\)の減光が起こることを表す式です。 今、散乱は無視できると考えて
\[S_\nu = \frac{\eta_\nu}{\kappa_\nu} = \frac{\epsilon_\nu^{ff}}{4\pi \alpha_\nu^{ff}} \tag{6}\]のように書けることを用いれば、観測される熱制動放射の強度は
\[I_\nu = \frac{2k_B}{c^2} T \nu^2 (1-e^{-\tau_\nu}) \tag{7}\]のようになります。
\(\tau_\nu \gg 1\)のとき
これは光学的厚さが非常に大きく、吸収の効果が大きく見込まれる場合に相当します。
\[I_\nu \simeq \frac{2k_B}{c^2} T \nu^2 \tag{8}\]のようになります。 これは黒体放射のレイリー・ジーンズ極限の式
\[B_\nu^\mathrm{RT} = \frac{2 k_B}{c^2} T \nu^2 \tag{9}\]に一致しています。
\(\tau_\nu \ll 1\)のとき
これは光学的厚さが非常に小さいため吸収は起こらない、すなわち熱制動放射そのものが見えるだろうという場合に相当します。
\[I_\nu \simeq \frac{2k_B}{c^2} T \nu^2 \left\{ 1 - (1-\tau_\nu)\right\} = \frac{2k_B}{c^2} T \nu^2 \alpha_\nu^{ff} \ell \tag{10}\]途中、光学的厚みの定義を用いた変形を行いました。 \(\ell\)は光線が進む距離を表します。 (4)式より、結局この場合は
\[I_\nu \propto T^{-1/2} \tag{11}\]のように、振動数に依存しない形となります。
正確にはガウントファクターが持つ振動数依存性が存在します。
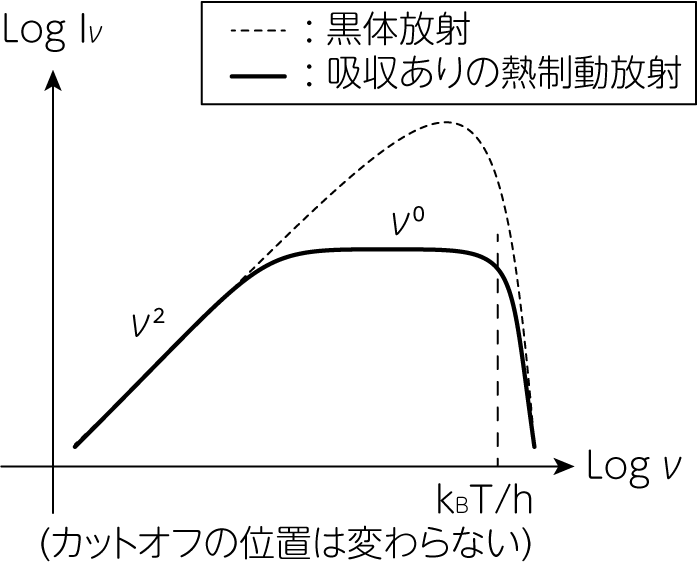
この形は熱制動放射の放射率において\(h \nu \ll k_B T\)とした場合に等しくなります。 以上のことから、熱制動吸収も含めた熱制動放射のスペクトルは下図のようになります。
参考文献
[1] Rybicki & Lightman, “Radiative Processes in Astrophysics”
[2] Dallacasa, “Processi di Radiazione e MHD, L03_Br.pdf”
[3] PHYS 780: Solar Flares and CMEs: Their PHysics and Observations, Lecture Note 20, “Impulsive phase fundamentals: Radiative processes I: bremsstrahlung”
[4] 鶴, “宇宙物理入門”講義資料, 第8章: 熱制動輻射と銀河・銀河団の高温プラズマ