Table of contents
Lienardの式とLarmorの式
電荷\(q\)の粒子の加速運動によって作られる輻射場は
\[\mathbf{E} (\mathbf{r} , t) = \frac{q}{c} \left[ \frac{\mathbf{g}}{R}\right] \tag{1}\]のように書かれました。ここで
\[\boldsymbol{\beta} (t) = \frac{\mathbf{u} (t)}{c}, \ \mathbf{g} = \frac{1}{\kappa^3} \mathbf{n} \times \{ (\mathbf{n}-\boldsymbol{\beta}) \times \dot{\boldsymbol{\beta}}\}, \ R (t') = |\mathbf{r}-\mathbf{r}_0 (t')|, \ \mathbf{n} (t') = \frac{\mathbf{r}-\mathbf{r}_0(t')}{R (t')}, \ \kappa (t) = 1-\mathbf{n} (t) \cdot \boldsymbol{\beta} (t)\]などです。\(\mathbf{r}_0 (t')\)は遅延時刻\(t'\)での電荷の位置、\(\mathbf{r}\)は観測者の位置ベクトルです。以下、観測者は荷電粒子から十分遠方におり、粒子から観測者までの距離\(R\)と\(\mathbf{n}\)の粒子の運動による変化を無視できるとします。観測者が受信する粒子からの放射の、単位立体角・単位時間あたりの強度は
\[\frac{dW}{dt d\Omega} = \frac{c}{4\pi} [R^2 E^2] \tag{2}\]となります。これを受信強度(received power)と呼び、\(\frac{dP_r}{d\Omega}\)と書きます。
ドップラー効果
粒子が\(t'\)から\(t'+dt'\)にかけて放射した電磁波を観測者は\(t\)から\(t+dt\)に受け取ったとします。
\[t = t' + \frac{R(t')}{c}, \quad t+dt =t'+dt' +\frac{R(t'+dt')}{c}\]これらより
\[dt =dt'+\frac{1}{c}(R(t'+dt')-R(t')) = dt'+\frac{1}{c} \frac{\partial R}{\partial t'}dt'\]途中、\(dt, dt' \ll 1\)としました。 これより
\[\frac{\partial R}{\partial t'} = \frac{\partial}{\partial t'} |\mathbf{r}- \mathbf{r}_0(t')| = \frac{\mathbf{r}- \mathbf{r}_0(t')}{|\mathbf{r}- \mathbf{r}_0(t')|} \cdot \left(-\frac{\partial \mathbf{r}_0}{\partial t'} \right) = -\mathbf{n} \cdot \mathbf{u}\]よって
\[dt = dt'(1-\mathbf{n} \cdot \frac{\mathbf{u}}{c}) = \kappa dt' \tag{3}\]Emitted power (放射強度)
粒子が単位時間あたりに放射した電磁波強度を放射強度(emitted power)と呼び、\(\frac{dP_e}{d\Omega}\)と書きます。これを求めてみましょう。
単位時間・単位面積あたりに輻射が運ぶエネルギーは、ポインティングベクトルの大きさに等しいです。よって微小面積を\(dA\)とすると
\(dA = [R^2] d\Omega\)より、観測者が受信する粒子からの単位立体角あたりの放射強度(recieved power)は
\[\frac{dP_r}{d\Omega} = \frac{d W}{dt d\Omega} = \frac{c}{4\pi} [R^2 E^2]\]となります。また、放射強度はその定義から
\[\frac{dP_e}{d\Omega} = \frac{dW}{dt'd\Omega}\]です。(3)式より
\[\frac{d P_e}{d\Omega} = \frac{[\kappa]}{dt}\frac{dW}{d\Omega} = \frac{c}{4\pi}[\kappa R^2 E^2] \tag{4}\]のように書かれることがわかります。
全放射強度
(4)式を全立体角積分すれば、全放射強度を得ることができます。
\[P_e = \frac{c}{4\pi} \int d\Omega [\kappa R^2 E^2] = \frac{c}{4\pi} \int d\Omega [\kappa g^2] \tag{5}\]計算を進めるために\(\mathbf{u}\)を\(z\)軸にとります。また\(\dot{\mathbf{u}}\)が\(xz\)平面内に来るような座標を設定し、\(\mathbf{u}\)とのなす角を\(i\)とします。また観測者は\(\mathbf{n} = (\sin \theta \cos \phi, \sin \theta \sin \phi, \cos \theta)\)方向にいるとします。
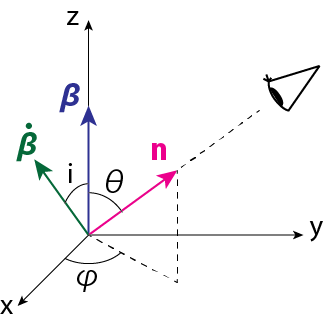
\(x, y, z\)方向の単位ベクトルをそれぞれ\(\mathbf{e}_x, \mathbf{e}_y, \mathbf{e}_z\)とします。先ほどの座標設定より\(\boldsymbol{\beta} = \beta \mathbf{e}_z, \dot{\boldsymbol{\beta}} = \dot{\beta}(\sin i \mathbf{e}_x+\cos i \mathbf{e}_z), \mathbf{n} = \sin \theta \cos \phi \mathbf{e}_x + \sin \theta \sin \phi \mathbf{e}_y + \cos \theta \mathbf{e}_z\)となります。これらより
\[\mathbf{n} \cdot \boldsymbol{\beta} = \beta \cos \theta \tag{6}\] \[\mathbf{n} \cdot \dot{\boldsymbol{\beta}} = \dot{\beta}( \sin \theta \cos \phi \sin i + \cos \theta \cos i) \tag{7}\] \[{\boldsymbol{\beta}} \cdot \dot{\boldsymbol{\beta}} = \beta \dot{\beta} \cos i \tag{8}\] \[\begin{align} \mathbf{g} &= \frac{1}{\kappa^3}\left\{ (\mathbf{n} \cdot \dot{\boldsymbol{\beta}})(\mathbf{n} - \boldsymbol{\beta}) - (\mathbf{n} \cdot (\mathbf{n} - \boldsymbol{\beta})) \dot{\boldsymbol{\beta}} \right\} = \frac{1}{\kappa^3} (\mathbf{n} \cdot \dot{\boldsymbol{\beta}})(\mathbf{n} - {\boldsymbol{\beta}}) - \frac{1}{\kappa^3}\underbrace{(1-\mathbf{n} \cdot {\boldsymbol{\beta}})}_{\kappa} \dot{\boldsymbol{\beta}} \notag \\ &= \frac{1}{\kappa^3} (\mathbf{n} \cdot \dot{\boldsymbol{\beta}})(\mathbf{n} - {\boldsymbol{\beta}}) - \frac{1}{\kappa^2}\dot{\boldsymbol{\beta}} \tag{9} \end{align}\]などが計算できます。さらにローレンツ因子\(\gamma = 1/ \sqrt{1-\beta^2}\)を用いると
\[\begin{align} g^2 &= \frac{1}{\kappa^6} (\mathbf{n} \cdot \dot{\boldsymbol{\beta}})^2(\mathbf{n} - {\boldsymbol{\beta}})^2 -\frac{2}{\kappa^5} (\mathbf{n}\cdot \dot{\boldsymbol{\beta}})\left\{ (\mathbf{n} - {\boldsymbol{\beta}}) \cdot \dot{\boldsymbol{\beta}}\right\}+ \frac{1}{\kappa^4}\dot{\beta}^2 \notag \\ &= \frac{1}{\kappa^6} (\mathbf{n} \cdot \dot{\boldsymbol{\beta}})^2(1- 2 \mathbf{n} \cdot {\boldsymbol{\beta}} + \beta^2) -\frac{2}{\kappa^5} (\mathbf{n}\cdot \dot{\boldsymbol{\beta}}) (\mathbf{n} \cdot \dot{\boldsymbol{\beta}}- {\boldsymbol{\beta}}\cdot \dot{\boldsymbol{\beta}}) + \frac{1}{\kappa^4}\dot{\beta}^2 \notag \\ &= \frac{1}{\kappa^6} (\mathbf{n} \cdot \dot{\boldsymbol{\beta}})^2(1- 2 \mathbf{n} \cdot \boldsymbol{\beta} + \beta^2 - 2\kappa) + \frac{2}{\kappa^5} (\mathbf{n}\cdot \dot{\boldsymbol{\beta}}) (\boldsymbol{\beta} \cdot \dot{\boldsymbol{\beta}}) + \frac{1}{\kappa^4}\dot{\beta}^2 \notag \\ &= \frac{1}{\kappa^6} (\mathbf{n} \cdot \dot{\boldsymbol{\beta}})^2 \underbrace{(-1+ \beta^2)}_{-\gamma^{-2}} + \frac{2}{\kappa^5} (\mathbf{n}\cdot \dot{\boldsymbol{\beta}}) (\boldsymbol{\beta} \cdot \dot{\boldsymbol{\beta}}) + \frac{1}{\kappa^4}\dot{\beta}^2 \notag \\ &= - \frac{1}{\kappa^6} (\mathbf{n} \cdot \dot{\boldsymbol{\beta}})^2 \gamma^{-2} + \frac{2}{\kappa^5} (\mathbf{n}\cdot \dot{\boldsymbol{\beta}}) (\boldsymbol{\beta} \cdot \dot{\boldsymbol{\beta}}) + \frac{1}{\kappa^4}\dot{\beta}^2 \tag{10} \end{align}\]以上より
\[\begin{align} \kappa g^2 = &\dot{\beta}^2 \left\{ \frac{1}{\kappa^3} + \frac{2}{\kappa^4} \beta (\sin \theta \cos \phi \sin i \cos i + \cos \theta \cos^2 i) \right. \notag \\ & \left. - \frac{1}{\kappa^5} \gamma^{-2} (\sin^2 \theta \cos^2\phi \sin^2 i + \cos^2 \theta \cos^2 i + 2\sin \theta \cos \theta \cos \phi \sin i \cos i) \right\} \tag{11} \end{align}\]となります。
積分を実行する上で必要となる、次の積分も計算しておきましょう。
これを\(\beta\)で微分したものを計算します。
\[\frac{d I_n}{d\beta} = \int_{-1}^1 d\mu \frac{d}{d\beta} \frac{1}{(1-\beta \mu)^n} = \int_{-1}^1 d\mu (-n)(-\mu) \frac{1}{(1-\beta \mu)^{n+1}} = n \int_{-1}^1d\mu \frac{\mu}{(1-\beta\mu)^{n+1}}\]これの最右辺の積分部分を\(J_{n+1}\)と定義します。
\[J_{n+1} \equiv \int_{-1}^1d\mu \frac{\mu}{(1-\beta\mu)^{n+1}} =\frac{1}{n} \frac{d I_n}{d\beta} \tag{13}\]さらにこれを\(\beta\)で微分したものを計算すると
\[\frac{dJ_n}{d\beta} = \int_{-1}^1d\mu \frac{d}{d\beta} \frac{\mu}{(1-\beta\mu)^{n+1}} = \int_{-1}^1\mu (-n)(-\mu) \frac{1}{(1-\beta\mu)^{n+1}} = n \int_{-1}^1 d\mu \frac{\mu^2}{(1-\beta\mu)^{n+1}}\]そしてこれの最右辺の積分部分を\(K_{n+1}\)と定義します。
\[K_{n+1} \equiv \int_{-1}^1d\mu \frac{\mu^2}{(1-\beta\mu)^{n+1}} =\frac{1}{n} \frac{d J_n}{d\beta} \tag{14}\]これで計算を進めるにあたって必要な材料が揃いました。それでは\(\kappa g^2\)の全立体角積分を行いましょう。そこで、以降では全立体角積分を
\[\int_{4\pi} d\Omega = \int_0^\pi d\theta \int_0^{2\pi} d\phi \sin \theta \underbrace{=}_{\mu = \cos \theta} \int_0^{2\pi} d\phi \int_{-1}^1 d\mu \tag{15}\]のように書き換えた形で行います。\(\kappa = 1- \mathbf{n} \cdot \boldsymbol{\beta} = 1-\beta \cos \theta = 1-\beta \mu\)より
\[\int_{4\pi} d\Omega \frac{1}{\kappa^3} = \int_0^{2\pi} d\phi \int_{-1}^1 d\mu \frac{1}{(1-\beta\mu)^3} = 2\pi I_3 \tag{16}\] \[\int_{4\pi} d\Omega \frac{1}{\kappa^4} \sin \theta \cos \phi \sin i \cos i = \sin i \cos i \underbrace{\int_0^{2\pi} d\phi \cos \phi}_{0}\int_{-1}^1 d\mu \frac{\sqrt{1-\mu^2}}{(1-\beta\mu)^4} = 0 \tag{17}\] \[\int_{4\pi} d\Omega \frac{1}{\kappa^4} \cos \theta \cos^2 i = \cos^2 i \int_0^{2\pi} d\phi \int_{-1}^1 d\mu \frac{\mu}{(1-\beta\mu)^4} =2\pi \cos^2 i J_4 \tag{18}\] \[\begin{align} \int_{4\pi} d\Omega \frac{1}{\kappa^5} \sin^2 \theta \cos^2 \phi \sin^2 i &= \sin^2 i\int_0^{2\pi} d\phi \cos^2 \phi \int_{-1}^1 d\mu \frac{1-\mu^2}{(1-\beta\mu)^5} \notag \\ &=\sin^2 i \int_0^{2\pi} d\phi \frac{1+ \cos 2\phi}{2} (I_5-K_5) = \pi \sin^2 i (I_5-K_5) \tag{19} \end{align}\] \[\int_{4\pi} d\Omega \frac{1}{\kappa^5} \sin \theta \cos \theta \cos \phi \sin i \cos i= \sin i \cos i \underbrace{\int_0^{2\pi} d\phi \cos \phi}_{0} \int_{-1}^1 d\mu \frac{\mu \sqrt{1-\mu^2}}{(1-\beta\mu)^5} = 0 \tag{20}\] \[\int_{4\pi} d\Omega \frac{1}{\kappa^5} \cos^2 \theta \cos^2 i = \cos^2 i \int_0^{2\pi} d\phi \int_{-1}^1 d\mu \frac{\mu^2}{(1-\beta\mu)^5} = 2\pi \cos^2 i K_5 \tag{21}\]以上を用いて
\[\begin{align} P_e &= \frac{q^2}{4\pi c} \int_{4\pi} d\Omega [\kappa g^2] = \frac{q^2}{4\pi c} \left[ \dot{\beta}^2\left\{ 2\pi I_3 + 2\beta \cdot 2\pi \cos^2 i J_4 - \gamma^{-2} (\pi \sin^2 i (I_5 -K_5)+ 2\pi \cos^2 i K_5)\right\} \right] \notag \\ &= \frac{q^2}{4\pi c} 2\pi \left[ \dot{\beta}^2\left\{I_3 + 2\beta (1-\sin^2 i)J_4 - \gamma^{-2} (\frac{1}{2} \sin^2 i (I_5 -K_5)+ (1-\sin^2 i) K_5)\right\}\right] \notag \\ &= \frac{q^2}{4\pi c} 2\pi \left[ \dot{\beta}^2\left\{I_3 + 2\beta J_4 -2\beta \sin^2 i J_4 - \gamma^{-2} K_5 -\frac{1}{2\gamma^2} (I_5 -3K_5)\sin^2 i \right\}\right] \notag \\ &= \frac{q^2}{4\pi c} 2\pi \left[ \dot{\beta} \left\{I_3 + 2\beta J_4 - \gamma^{-2} K_5 -(2\beta J_4 + \frac{1}{2\gamma^2} (I_5 -3K_5)) \sin^2 i\right\}\right] \notag \\ &= \frac{q^2}{4\pi c} 2\pi \left[ \dot{\beta} \left\{I_3 + 2\beta \frac{1}{3}\frac{d I_3}{d\beta} - \gamma^{-2} \frac{1}{4} \frac{d J_4}{d\beta} -(2\beta \frac{1}{3}\frac{d I_3}{d\beta} + \frac{1}{2\gamma^2} (I_5 -3\frac{1}{4} \frac{d J_4}{d\beta})) \sin^2 i\right\}\right] \notag \\ &= \frac{q^2}{4\pi c} 2\pi \left[ \dot{\beta} \left\{I_3 +\frac{2}{3}\beta \frac{d I_3}{d\beta} - \frac{1}{4 \gamma^2} \frac{1}{3}\frac{d^2 I_3}{d\beta^2} -(\frac{2}{3} \beta \frac{d I_3}{d\beta} + \frac{1}{2\gamma^2} (I_5 -\frac{3}{4} \frac{1}{3}\frac{d^2 I_3}{d\beta^2})) \sin^2 i\right\}\right] \tag{22} \end{align}\]途中で出てきた\(I, J, K\)を具体的に計算しましょう。
\[I_3 = \frac{(1+\beta)^2-(1-\beta)^2}{2\beta (1-\beta^2)^2} = \frac{4\beta}{2\beta(1-\beta^2)^2} = \frac{2}{(1-\beta^2)^2} =2\gamma^4 \tag{23}\] \[\begin{align} I_5 &= \frac{(1+\beta)^4-(1-\beta)^4}{4\beta (1-\beta^2)^2} = \frac{(1+4\beta+ 6\beta^2+ 4\beta^3 + \beta^4)-(1-4\beta+ 6\beta^2 -4\beta^3 + \beta^4)}{4\beta (1-\beta^2)^4} \notag \\ &= \frac{8\beta + 8\beta^3}{4\beta(1-\beta^2)^4} = 2(1+\beta^2 )\gamma^8 \tag{24} \end{align}\] \[\frac{dI_3}{d\beta} = \frac{-2 \cdot 2(1-\beta^2) (-2\beta)}{(1-\beta^2)^4} = \frac{8\beta}{(1-\beta^2)^3} = 8\beta \gamma^6 \tag{25}\] \[\begin{align} \frac{d^2 I_3}{d\beta^2} &= 8 \frac{d}{d\beta} \frac{\beta}{ (1-\beta^2)^3} = 8\frac{(1-\beta^2)^3 - \beta \cdot 3(1-\beta^2)^2 (-2\beta)}{(1-\beta^2)^6} = 8\frac{1-\beta^2 + 6\beta^2}{(1-\beta^2)^4} \notag \\ &= 8 \frac{1+5\beta^2}{(1-\beta^2)^4} = 8(1+5\beta^2)\gamma^8 \tag{26} \end{align}\]こうして、求めたかった全放射強度は
\[\begin{align} P_e &= \frac{q^2}{4\pi c} 2\pi [ \dot{\beta} \{I_3 +\frac{2}{3}\beta \cdot 8\beta \gamma^6 - \frac{1}{12 \gamma^2}8(1+5\beta^2)\gamma^8 \notag \\ &-\left(\frac{2}{3} \beta \cdot 8\beta \gamma^6 + \frac{1}{2\gamma^2} (2(1+\beta^2)\gamma^8 -\frac{1}{4}8(1+5\beta^2)\gamma^8)\right) \sin^2 i \} ] \notag \\ &= \frac{q^2}{4\pi c} 2\pi \left[ \dot{\beta}^2 \left\{ 2\gamma^4 + \frac{16}{3} \beta^2 \gamma^6 -\frac{2}{3} (1+5\beta^2) \gamma^6 -(\frac{16}{3} \beta^2 \gamma^6 -4 \gamma^6 \beta^2)\sin^2 i \right\} \right] \notag \\ &= \frac{q^2}{4\pi c} 2\pi \left[ \dot{\beta}^2 \left( 2\gamma^4 + 2\beta^2 \gamma^6 -\frac{2}{3}\gamma^6 -\frac{4}{3} \beta^2 \gamma^6 \sin^2 i\right) \right] \notag \\ &= \frac{q^2}{4\pi c} 2 \pi \left[ \dot{\beta}^2 \gamma^6 \left( 2\gamma^{-2} + 2\beta^2 - \frac{2}{3} -\frac{4}{3} \beta^2 \sin^2 i\right)\right] \notag \\ &\underbrace{=}_{\gamma^{-2} = 1-\beta^2} \frac{q^2}{4\pi c} 2\pi \left[ \dot{\beta}^2 \gamma^6 \left( 2-\frac{2}{3} -\frac{4}{3}\beta^2 \sin^2 i\right)\right] \notag \\ &= \frac{2q^2}{3c^3} \left[ \dot{u}\gamma^6 (1-\beta^2 \sin^2 i)\right] \tag{27} \end{align}\]角度\(i\)の定義より
\[|\dot{\mathbf{u}} \times \boldsymbol{\beta}| = \dot{u} \beta \sin i\]から
\[P_e = \frac{2q^2}{3c^3}\left[ \gamma^6 (\dot{u}^2 - \left| \dot{\bf u} \times \boldsymbol{\beta} \right|^2)\right] \tag{28}\]これをリエナー(Liénard)の式と呼びます。
非相対論的極限
粒子の運動が非相対論的なとき、\(\gamma \rightarrow 1, \boldsymbol{\beta} \rightarrow \mathbf{0}\)です。さらに\(t_\mathrm{ret} = t\)として
\[P_e = \frac{2q^2}{3c^3} \dot{u}^2 \tag{29}\]これはラーモア(Larmor)の式と呼ばれるものです。 非相対論的な場合の輻射場の詳細を調べましょう。 非相対論的であるため、\(\beta \sim 0\)として、輻射場を\(\beta\)の一次までで近似すると
\[\mathbf{E}_\mathrm{rad} = \left[ \frac{q}{c^2 R} \mathbf{n} \times (\mathbf{n} \times \dot{\mathbf{u}})\right]tag{30}\]のようになります。 このとき、\(\mathbf{n}, \mathbf{E}_\mathrm{rad}, \dot{\mathbf{u}}\)の向きの関係を図示すると、以下のようになります。

上図のように\(\mathbf{n}, \dot{\mathbf{u}}\)の成す角を\(\Theta\)とすると、電場・磁場の大きさは
\[\mathbf{E}_\mathrm{rad} = \mathbf{B}_\mathrm{rad} = \left[ \frac{q\dot{u}}{c^2 R} \sin \Theta \right] \tag{31}\]これらを(4)式に代入すれば
\[\frac{dP}{d\Omega} = \frac{dW}{dt d\Omega} = [R^2 S] = \left[ \frac{q^2 \dot{u}^2}{4\pi c^3} \sin^2 \Theta\right] \tag{32}\]のように求まります。
次に、放射の周波数分布を求めましょう。 この系の双極子モーメントを\(\mathbf{d}(t') = q \mathbf{r}_0(t')\)とすれば、(31)式より輻射場の電場の振幅は
のように書けます。 ここで双極子モーメントを以下のようにフーリエ積分表示すると、その2階微分は
\[d(t) = \int_{-\infty}^\infty \hat{d}(\omega) e^{-i\omega t} d\omega \ \Longrightarrow \ \ddot{d} (t) = \int_{-\infty}^\infty (-\omega^2) \hat{d} (\omega) e^{-i\omega t} d\omega \tag{34}\]と計算されます。 さらに左辺の電場振幅も
\[E(t) = \int_{-\infty}^\infty \hat{E}(\omega) e^{-i\omega t} d\omega \tag{35}\]のようにフーリエ積分表示の形に書き、両辺を見比べれば
\[\hat{E} (\omega) = -\frac{\omega^2 \hat{d}(\omega)}{c^2 R} \sin \Theta \tag{36}\]のように書くことができます。 ここで、荷電粒子は十分遠くにあるとし、\(R\)の時間変化を無視しました。 (36)式は、非相対論的な運動をする荷電粒子からの輻射の周波数は、粒子の振動の周波数と同じであることを意味します。 このことは、荷電粒子の運動が非相対論的であるとして、輻射場を\(\beta\)の最低次までしか残さない近似をしたことに関係します。 実際には輻射場の式(1)を\(\beta\)でテイラー展開すると、\(\beta^2\)のような高次の項が出現します。 簡単のため荷電粒子が振動数\(\omega_0\)で振動している場合を考えると、例えば2次の項は
\[\beta \dot{\beta} \propto \cos \omega_0 t \sin \omega_0 t \propto \sin 2 \omega_0 t \tag{37}\]という寄与をもたらすことになります。 このことから、2次の項は\(\omega = 2\omega_0\)の2倍の周波数を持つ電磁波の生成に結びつきます。 さらに高次の項を考慮すれば、さらに高調波が生まれます。
横道に逸れましたが、(36)式より単位周波数あたりの全放射エネルギーの角度分布は
となり、さらに単位周波数あたりの全放射エネルギーはこれを全立体角積分することで
\[\begin{align} \frac{dW}{d\omega} &= \frac{\omega^4 \left| \hat{d} (\omega) \right|^2}{c^3} \int \sin^2 \Theta d\Omega = \frac{2\pi \omega^4 \left| \hat{d} (\omega) \right|^2}{c^3} \int_0^\pi (1-\cos^2 \Theta) \sin \Theta d \Theta \notag \\ &\underbrace{=}_{\mu = \cos \Theta} \frac{2\pi \omega^4 \left| \hat{d} (\omega) \right|^2}{c^3} \int_{-1}^1 (1-\mu^2) d\mu = \frac{8\pi \omega^4 \left| \hat{d} (\omega) \right|^2}{3c^3} \tag{39} \end{align}\]のように求まります。