Table of contents
ロッシュローブ
2つの恒星の質量が\(M_1, M_2\)であるような連星系を考え、その連星系の周りの流体の運動を調べましょう。この問題をロッシュ(Roche)問題と呼びます。以下での流体の運動を、お互いに軌道運動をしている2つの恒星が作るポテンシャル中のテスト粒子の運動と同等であるとして調べます。すなわち制限3体問題として扱い、テスト粒子は連星の軌道運動には影響を与えないと仮定します。2つの恒星はお互いに円運動をしているものとし、ポテンシャル計算にあたっては恒星は質点として扱います。
ケプラーの法則と軌道半径の見積もり
軌道半径\(a\)、公転周期\(\Pi\)の連星系では、ケプラーの法則が成り立ちます。
\[4\pi^2 a^3 = G(M_1 + M_2) \Pi^2 \tag{1}\]ここで2つの質量比を\(q \equiv M_2 / M_1\)とおくと
\[a^3 = \frac{GM_1 (1+q)}{4\pi^2} \Pi^2 = \frac{c^2}{8\pi^2} \frac{2 GM_\odot}{c^2} \frac{M_1}{M_\odot} (1+q) \Pi^2 \simeq \frac{3}{8} \times 10^{25} \frac{M_1}{M_\odot} (1+q) \Pi^2\]\(\Pi\)を\(1 \mathrm{yr} = \pi \times 10^7 \mathrm{s}\)で規格化して表現した場合
\[\begin{align} &a^3 = \frac{c^2}{8\pi^2} \frac{2 GM_\odot}{c^2} \frac{M_1}{M_\odot} (1+q) \left( \frac{\Pi}{1 [\mathrm{yr}]}\right)^2 \pi^2 \times 10^{14} \simeq \frac{27}{8} \times 10^{39} \frac{M_1}{M_\odot} (1+q) \left( \frac{\Pi}{1 \mathrm{yr}}\right)^2 \notag \\ &\Longrightarrow \ a \simeq 1.5 \times 10^{13} \left( \frac{M_1}{M_\odot} \right)^{1/3} (1+q)^{1/3} \left( \frac{\Pi}{1 \mathrm{yr}}\right)^{2/3} [\mathrm{cm}] \tag{2} \end{align}\]となります。\(1 \mathrm{AU} \sim 1.5 \times 10^{13}\)cmなので、\(M_1 = M_\odot, \Pi = 1 \mathrm{yr}\)のときには、連星の距離は\(1\mathrm{AU}\)であるとわかります。
コンパクト連星では軌道周期が数日、数時間、数分といった場合があります。その場合にはそれぞれ
のようになります。軌道周期が数分の場合には、その軌道半径は太陽半径\(R_\odot \sim 6.96 \times 10^{10}\)cm程度であることもわかります。
ロッシュポテンシャル
連星系の質量中心(重心)を座標原点とし、その原点の周りを公転周期\(\Pi\)で回転する座標系に乗って考えましょう。連星系の重力場中における、質量\(m=1\)のテスト粒子の運動方程式は
\[\frac{d\mathbf{v}}{dt} = - \nabla \Phi_R - 2 \boldsymbol{\Omega} \times \mathbf{v} \tag{6}\]のようになります。ここで
\[\Omega = \sqrt{\frac{GM_1 (1+q)}{a^3}} \tag{7}\]は連星の公転振動数\(\Omega = 2\pi /\Pi\)、そして
\[\Phi_R = - \frac{GM_1}{|\mathbf{r}-\mathbf{r}_1|} - \frac{GM_2}{|\mathbf{r}-\mathbf{r}_1|} - \frac{1}{2} (\boldsymbol{\Omega} \times \mathbf{r})^2 \tag{8}\]はこの系でのポテンシャルです。回転系で考えているため、(6)式にはコリオリ力、(8)式には遠心力によるポテンシャルが出現しています。\(\mathbf{r}_1, \mathbf{r}_2\)はそれぞれ原点から測った連星を構成する恒星の位置ベクトルです。以下では\(\boldsymbol{\Omega}\)は連星の軌道面と垂直な方向に向いていると考えます。
軌道面に垂直な方向を\(z\)方向と定めます。さらに軌道面内において2つの恒星を結ぶ直線を\(x\)軸とし、それに垂直に\(y\)軸を取ります。まずは、この座標系における連星の位置を求めましょう。ここまでの座標の取り方より、重心は
ここで
\[\alpha \equiv \frac{1}{1+q}, \quad \beta \equiv \frac{q}{1+q} \tag{10}\]としました。連星系はお互いに円運動をしており、その軌道半径は\(a\)としたので
\[x_1 - x_2 = a \ \Longrightarrow \ x_1 + \frac{\alpha}{\beta} x_1 = \frac{\alpha + \beta}{\beta} x_1 = \frac{x_1}{\beta} = a \ \Longrightarrow \ x_1 = \beta a\tag{11}\]とわかります。同様に
\[-\frac{\beta}{\alpha} x_2 - x_2 = - \frac{\alpha + \beta}{\alpha} x_2 = - \frac{x_2}{\alpha} = a \ \Longrightarrow \ x_2 = -\alpha a \tag{12}\]となります。ここで\(i\)方向の単位ベクトルを\(\mathbf{e}_i\)とすると\(\mathbf{r} = x \mathbf{e}_x + y \mathbf{e}_y + z \mathbf{e}_z\)、そして\(\mathbf{r}_1 = x_1 \mathbf{e}_x, \mathbf{r}_2 = x_2 \mathbf{e}_x\)のように書かれます。さらに問題設定から\(\boldsymbol{\Omega} = \Omega \mathbf{e}_z\)より、(8)式は
\[\Phi_R = - \frac{GM_1}{\sqrt{(x-\beta a)^2 + y^2 + z^2}} - \frac{GM_2}{\sqrt{(x+\alpha a)^2 + y^2 + z^2}} -\frac{1}{2} (\Omega^2 x^2 + \Omega^2 y^2)\]座標系を軌道半径で規格化し、\(X = x / a, Y = y/a, Z = z/a\)とすると
\[\begin{align} \Phi_R &= - \underbrace{\frac{G(M_1 + M_2)}{a}}_{= a^2 \Omega^2} \left( \frac{\alpha}{\sqrt{(X-\beta)^2 + Y^2 + Z^2}} + \frac{\beta}{\sqrt{(X+\alpha)^2 + Y^2 + Z^2}}\right) - \frac{1}{2} \Omega^2 a^2 (X^2 + Y^2) \notag \\ &= a^2 \Omega^2 \Psi_\mathrm{eff} \tag{13} \end{align}\]のように書かれます。途中
\[\Psi_\mathrm{eff} \equiv - \left\{ \frac{\alpha}{\sqrt{(X-\beta)^2 + Y^2 + Z^2}} + \frac{\beta}{\sqrt{(X+\alpha)^2 + Y^2 + Z^2}} + \frac{1}{2} (X^2 + Y^2) \right\} \tag{14}\]のように、規格化された有効ポテンシャルを定義しました。有効ポテンシャルを可視化すると以下のようになります。一つ目は\(q=0.5\)の場合です。
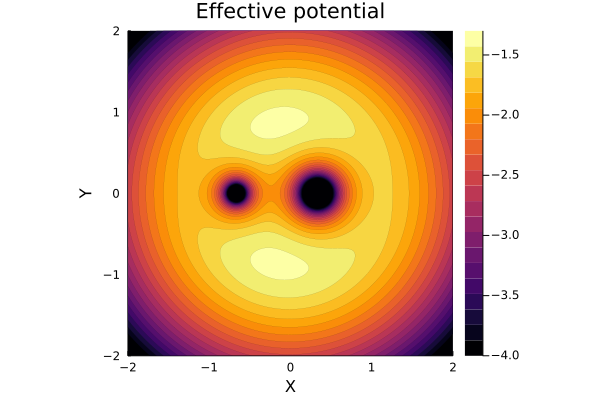
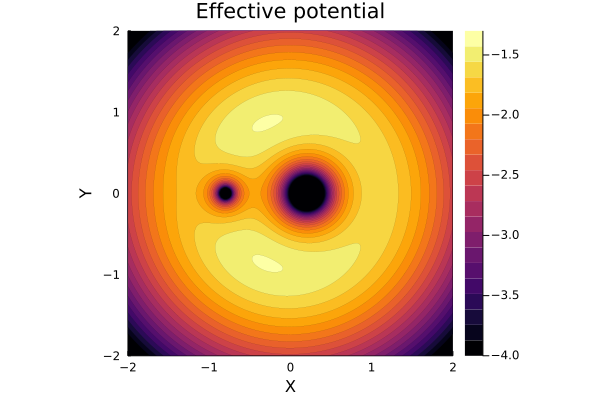
次に\(q-0.25\)の場合です。2つの恒星質量の偏りが大きくなり、それに伴ってポテンシャルの形状も変化しています。
連星を結ぶ直線上にあるラグランジュ点
この連星系におけるラグランジュ点(ポテンシャルの勾配が0となる点)を、\(X\)軸上の場合に求めてみましょう。(14)式において\(Y = Z = 0\)として、\(X\)で微分すると
\[\frac{\partial \Psi_\mathrm{eff}}{\partial X} = \frac{\alpha}{(X-\beta)^2} + \frac{\beta}{(X + \alpha)^2} - X \tag{15}\]これが0となるところが極値です。しかしこの式は(パッと見た感じでは)解析的に解くことは難しそうです。よって\(f(X) \equiv \frac{\partial \Psi_\mathrm{eff}}{\partial X}\)として、\(f(X = 0)\)となる解を探します。ニュートン法などを用いる場合、\(f(X)\)をもう一度微分する必要があります。すると
\[\frac{\partial f}{\partial X} = \frac{-2 \alpha}{(X-\beta)^3} + \frac{-2\beta}{(X+\alpha)^3} \tag{16}\]となります。(15), (16)式を用いてニュートン法で解を探すと、以下のようになります。
\[\begin{aligned} &q = 0.5 \ \cdots \ L_1 \sim -0.24, \quad L_2 \sim -1.25, \quad L_3 \sim 1.14 \\ &q = 0.25 \ \cdots \ L_1 \sim -0.44, \quad L_2 \sim -1.27, \quad L_3 \sim 1.08 \end{aligned}\]テスト粒子の運動
(6)式から、テスト粒子の運動を計算してみましょう。簡単のため、以下では\(xy\)平面内の軌道計算のみを行うものとします。計算を行いやすいように、時間を\(T = \frac{t}{1/\Omega}\)、長さ(座標)を\(X = \frac{x}{a}\)のように規格化すると
\[\frac{a}{1/\Omega^2}\frac{d^2 \mathbf{X}}{dT^2} = -\frac{1}{a} \nabla \Phi_R - 2 \Omega \frac{a}{1/\Omega} \mathbf{e}_z \times \frac{d \mathbf{X}}{dt} \ \Longrightarrow \ \frac{d^2 \mathbf{X}}{dT^2} = - \nabla \frac{\Phi_R}{a^2 \Omega^2} + 2 \left( \begin{array}{c} \frac{dY}{dt} \\ -\frac{dX}{dt} \end{array}\right) = - \nabla \Psi_\mathrm{eff} + 2 \left( \begin{array}{c} \frac{dY}{dt} \\ -\frac{dX}{dt} \end{array}\right)\]のようになります。\(u_1 = X, u_2 = Y, u_3 = \frac{dX}{dT}, u_4 = \frac{dY}{dT}\)とおくと、テスト粒子の位置・速度の時間発展は
\[\frac{d}{dT} \left( \begin{array}{c} u_1 \\ u_2 \\ u_3 \\ u_4 \end{array}\right) = \left( \begin{array}{c} u_3 \\ u_4 \\ -\frac{\partial \Psi_\mathrm{eff}}{\partial X} + 2 u_4 \\ -\frac{\partial \Psi_\mathrm{eff}}{\partial Y} - 2 u_3 \end{array}\right)\]のような連立微分方程式となります。これをルンゲ・クッタ法などを用いて時間積分すれば、数値的にテスト粒子の運動を解くことができます。 下図は\(q = 0.5\)、\(X, Y, v_X, v_Y\)の初期値をそれぞれ\(-0.24, 0.0, -0.01, 0.0\)のように、ラグランジュ点\(L_1\)から\(X\)軸負の方向に初速を与えた場合の軌道計算例です。
この場合、\(x_2 = -2/3\)に連星系を構成する星がいます。その星に向かって落下しつつも、回転座標系に乗っていることでコリオリ力が働き、複雑な軌道を描きます。
実際には、\(M_1\)の質量を持つ恒星1が主系列星から進化していくと、赤色巨星などのように外層が膨張するフェーズへと移行します。このとき、ロッシュローブから溢れ出したガスが\(L_1\)から\(M_2\)の質量を持つ恒星2へと降り注ぎます。このとき先の動画でも示したように、流体は直接恒星2に落ちるのではなく、角運動量を持つために恒星の周囲を軌道運動します。このようにして恒星2の周囲に降着円盤が形成されます。恒星2が白色矮星や中性子星であれば降着円盤は高温になり、X線などの高エネルギー波長で明るく輝きます。(3), (4), (5)式のように連星がかなり近接している場合には、その降着円盤のフラックスは連星軌道周期に合わせて数分-数日周期で変動します。
参考文献
- 柴田一成, 福江純, 松元亮治, 嶺重慎, “活動する宇宙”
- 小山勝二, 嶺重慎, “ブラックホールと高エネルギー現象”