Table of contents
スピンダウン
ここでは中性子星のおおよその年齢を推定する上で用いられる、スピンダウンについて議論します。
磁気モーメントからの放射
非相対論的な運動する点電荷からの放射は、ラーマーの式より
\[P_e = \frac{2q^2}{3c^3} \dot{\mathbf{u}}^2\]と記述されます。ここで\(q\)は点電荷の持つ電荷、そして\(\mathbf{u}= \dot{\mathbf{r}}\)は点電荷の速度ベクトルです。この系の電気双極子モーメントを\(\mathbf{d} = q \mathbf{r}\)とすると、先程の式は
\[P_e = \frac{2}{3c^3} \ddot{\mathbf{d}}^2\]ここから磁気モーメント\(\mathbf{m}\)が時間変化することによる放射を考えます。それは実は\(\mathbf{d} \rightarrow \mathbf{m}\)のように置き換えたものに等しく
\[P_m = \frac{2}{3c^3} \ddot{\mathbf{m}}^2 \tag{1}\]となります。
注意: この導出は厳密ではありません。もし厳密に求めたければ、適当な電磁気の教科書をご参照ください。
回転する中性子星からの放射
下図のように強磁場を持つ中性子星を磁気双極子モーメントに置き換えて考えます。
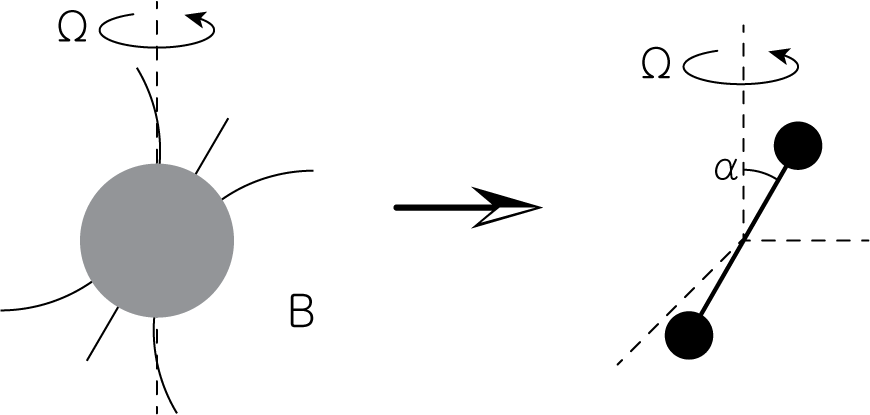
回転軸に対して\(\alpha\)だけ傾いた中性子星が角速度\(\Omega\)で回転していると考えましょう。その磁気モーメントは、回転軸を\(z\)軸に取ると
\[\mathbf{m} = m (\mathbf{e}_x \sin \alpha \cos \Omega t + \mathbf{e}_y \sin \alpha \sin \Omega t + \mathbf{e}_z \cos \alpha)\]のように書けます。ここで\(m\)は磁気モーメントの大きさで、この大きさは時間変化しないとします。これより
\[\ddot{\mathbf{m}} = - m \Omega^2 (\mathbf{e}_x \sin \alpha \cos \Omega t + \mathbf{e}_y \sin \alpha \sin \Omega t) \tag{2}\](1), (2)式より
\[P_m = \frac{2}{3c^3} \Omega^4 m^2 \sin^2 \alpha \tag{3}\]スピンダウンからの年齢の推定
(3)式で記述される輻射のエネルギー放出によって中性子星の回転のエネルギーが失われていくとすると
\[\frac{d}{dt} \left( \frac{1}{2} I \Omega^2\right) = - \frac{2}{3c^3} \Omega^4 m^2 \sin^2 \alpha\]のようになります。ここで\(I\)は中性子星の慣性モーメントです。右辺のマイナスにより、回転のエネルギーが失われていくことを表現しています。中性子星は孤立しており慣性モーメントはその進化において時間変化しないとすると、左辺は\(I \Omega \dot{\Omega}\)のように書けるので
\[\dot{\Omega} = - \frac{2m^2 \sin^2 \alpha}{3c^3 I} \Omega^3 = - K \Omega^3 \qquad (K \equiv \frac{2m^2 \sin^2 \alpha}{3c^3 I}) \tag{4}\]となります。これより
\[\dot{\Omega} \Omega^{-3} = -K \ \Longrightarrow \ - \frac{1}{2} (\Omega^{-2} - \Omega_0^{-2}) = -K(t-t_0)\]と計算されます。ここで\(\Omega_0\)は中性子星が誕生したときの回転角速度、そして\(t_0\)は中性子星が誕生した時刻です。よって右辺の\(\tau \equiv t-t_0\)は、中性子星の年齢を表しています。中性子星が十分昔に生まれ、現在の時刻においてその回転角速度がだいぶ小さくなったと仮定すると、\(\Omega_0^{-2} \ll \Omega^{-2}\)と近似できるので
\[\frac{1}{2} \Omega^{-2} \simeq K \tau \tag{5}\](4)式を用いて(5)式から\(K\)を消去すると
\[\frac{1}{2} \Omega^{-2} = - \dot{\Omega} \Omega^{-3} \tau\]ここで\(\Omega\)と回転周期\(P\)の関係より
\[\Omega = \frac{2\pi}{P} \ \Longrightarrow \ \dot{\Omega} = - \frac{2\pi}{P^2} \dot{P} \tag{6}\]を用いると
\[\tau = \frac{P}{2\dot{P}}\]さらに両辺の対数を取れば
\[\log \dot{P} = \log P - \log \tau + C \qquad (C: 定数) \tag{7}\]のようになります。よって横軸を\(\log P\)(中性子星の回転周期の対数)、縦軸を\(\log \dot{P}\)(中性子星の回転周期の時間変化の対数)としたときのグラフを描いたとき、\(\log \tau\)が\(y\)切片となるような傾きが正の直線となります。また\(\log \tau\)の係数が負であることから、直線が下に行くほど年齢が古くなります。
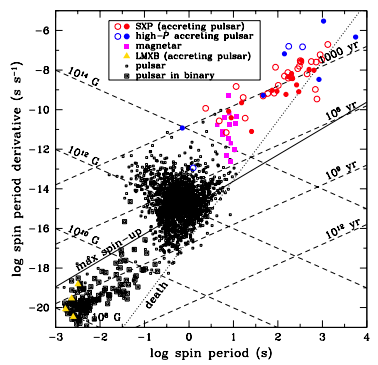
スピンダウンからの磁場の大きさの推定
途中までの式で
\[I \Omega \dot{\Omega} = - \frac{2}{3c^3} m^2 \Omega^4 \sin^2 \alpha\]とわかりました。ここに磁化\(m\)が作る磁場の大きさ\(B = \frac{m}{r^2}\)を代入すると
\[I \dot{\Omega} \Omega^{-3} = - \frac{2}{3c^3} B^2 R^6 \sin^2 \alpha\]ここに先程の(6)式を用いて式変形を行えば
\[B^2 = \frac{3c^3 I}{8\pi^2 R^6 \sin^2 \alpha} P \dot{P} \tag{8}\]となり、この両辺の対数を取れば
\[\log \dot{P} = - \log P + 2 \log B + D \qquad (D: 定数) \tag{9}\]を導くことができます。よって横軸を\(\log P\)(中性子星の回転周期の対数)、縦軸を\(\log \dot{P}\)(中性子星の回転周期の時間変化の対数)としたときのグラフを描いたとき、\(\log B\)が\(y\)切片となるような傾きが負の直線となります。また\(\log B\)の係数が正であることから、直線が上に行くほど磁場が強くなります(上図の点線参照)。
参考文献
[1] Ho et al., 2013, “Equilibrium spin pulsars unite neutron stara populations”
[2] 砂川重信, “理論電磁気学”