2.2 Radiative transfer equationの形式的な解

Source function \(S_\nu\)がoptical depthの関数として与えられている場合は、平行平板近似のもとでRadiative transferの式を形式的に解くことが可能です(形式的な解と言われるのは\(S_\nu(\tau_\nu)\)を得るのに\(I_\nu\)を知る必要があるからです)。
(2.5)式を変形します。

\[\begin{align} & \frac{dI_\nu}{d\left( \frac{\tau_\nu}{\mu} \right)} - I_\nu = -S_\nu \notag \\ & \Longrightarrow \ e^{-\frac{\tau_\nu}{\mu}} \frac{dI_\nu}{d\left( \frac{\tau_\nu}{\mu} \right)} - e^{-\frac{\tau_\nu}{\mu}} I_\nu = - e^{-\frac{\tau_\nu}{\mu}} S_\nu \notag \\ & \Longrightarrow \ \frac{d(I_\nu e^{-\frac{\tau_\nu}{\mu}})}{d\left( \frac{\tau_\nu}{\mu}\right)} = -S_\nu e^{-\frac{\tau_\nu}{\mu}} \tag{2.15} \end{align}\]

これを積分して

\[I_\nu (\tau_\nu, \mu) e^{-\frac{\tau_\mu}{\mu}} = I_\nu (\tau_{0\nu}, \mu) e^{-\frac{\tau_{0 \nu}}{\mu}} + \int_{\tau_\nu}^{\tau_{0\nu}} S_\nu (t) e^{-\frac{t}{\mu}} \frac{dt}{\mu} \tag{2.16}\]

または

\[I_\nu (\tau_\nu, \mu) = I_\nu (\tau_{0\nu}, \mu) e^{-\frac{\tau_{0\nu}-\tau_\nu}{\mu}} + \int_{\tau_\nu}^{\tau_{0\nu}} S_\nu (t) e^{-\frac{t-\tau_\nu}{\mu}} \frac{dt}{\mu} \tag{2.16'}\]

が得られます。この式は\(I_\nu (\tau_\nu, \mu)\)が、\(I_\nu (\tau_{0\nu}, \mu)\)に\((\tau_{0\nu}-\tau_\nu)\)間で起こる吸収の補正をしたものに、その間で起こる発光の効果を吸収の補正を加えたものであることを表しています。

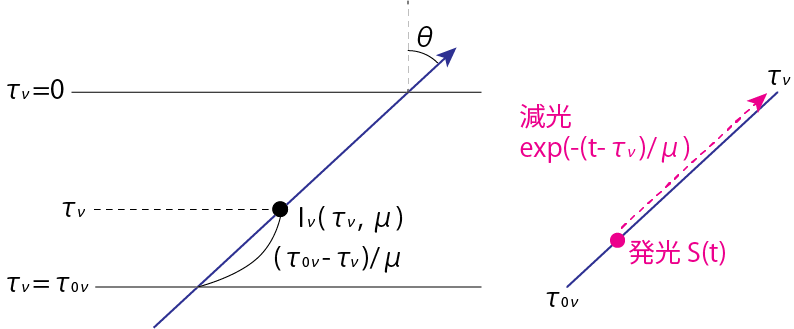
(2.16')式の意味。

2.2.1 Absorption line と Emission line

以下では簡単のため\(\mu=1, S_\nu = {\rm const}, \tau_\nu = 0\)とします。

\[I_\nu (0, 1) = I_\nu (\tau_{0\nu}, 1) e^{-\tau_{0\nu}} + S_\nu \int_0^{\tau_{0\nu}} e^{-t} dt = I_\nu (\tau_{0\nu}, 1) e^{-\tau_{0\nu}} + S_\nu (1-e^{-\tau_{0\nu}}) \tag{2.17}\]

のように表されます。ここで\(\tau_{0\nu}\)は考えているガス層の底のoptical depthです。ガス層のtopのoptical depthを0としているため、ガス層のoptical thickness \(\kappa_\nu \rho D = \tau_{0\nu}\)を表します。これは次の図の\(\tau_\nu (D)\)と同じ意味です。

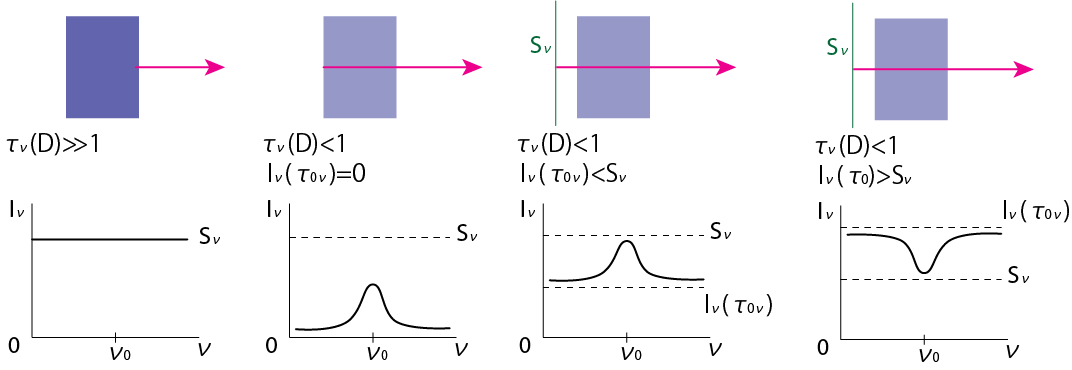
輝線や吸収線が形成される状況。

1. \(\tau_{0\nu}\gg 1\)のとき

\(e^{-tau_{0\nu}} \rightarrow 0\)なので、(2.17)式より

\[I_\nu (0) = S_\nu, \ {\rm LTE}では \ I_\nu (0) = B_\nu\]

となり、これは入射光のIntensity\(I_\nu (\tau_{0\nu})\)と吸収係数の詳細な形によらず連続スペクトルになることがわかります。これは恒星の光球から出てくる光に対応します。

2. \(\tau_{0\nu}<1\)のとき

\(e^{-\tau_{0\nu}}\)を展開することで、(2.17)式は

\[I_\nu (0) = I_\nu (\tau_{0\nu}) (1-\tau_{0\nu}) + S_\nu \tau_{0\nu} + \mathcal{O} (\tau_{0\nu}^2) = I_\nu (\tau_{0\nu}) + \tau_{0\nu} \left\{ S_\nu - I_\nu (\tau_{0\nu}) \right\} + \mathcal{O} (\tau_{0\nu}^2) \tag{2.18}\]

のように書けます。この場合のEmergent intensity \(I_\nu (0)\)は\(\tau_{0\nu} = \kappa_\nu \rho D\)に依存し、\(\kappa_\nu\)の大きい振動数に輝線(Emission line)または吸収線(Absorption line)が形成されます。

\(I_\nu (\tau_{0\nu}) < S_\nu\)のとき Emission line
\(I_\nu (\tau_{0\nu}) > S_\nu\)のとき Absorption line

となります。つまり光源を背景にして、その光源温度よりも温度の低い希薄(光学的厚さ<1)なガスがある場合には吸収線が形成されます。背景に光源が無いか、ガスの温度が光源よりも高いときには輝線が形成されます。