Table of contents
オールト定数
天の川銀河の回転とオールト定数
私たちの住む天の川銀河の回転の様子を調べるために、銀河面内の任意の位置にある光源の視線速度と接線速度のデータを解析することを考えましょう。
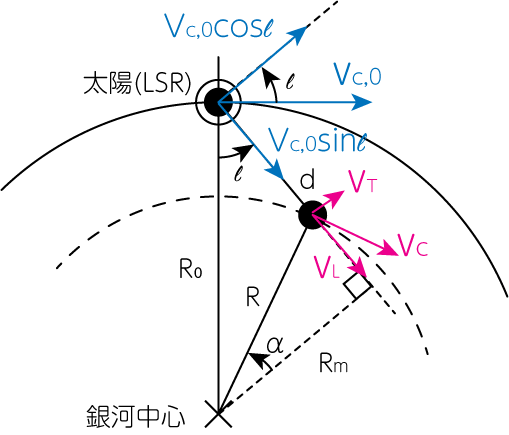
以上から
\[\cos \alpha = \frac{R_0}{R} \sin \ell = \frac{R_0 \Omega}{v_c} \sin \ell \tag{5}\] \[v_L = (\Omega - \Omega_0) R_0 \sin \ell \tag{6}\] \[v_T = (\Omega - \Omega_0) R_0 \cos \ell - \Omega d \tag{7}\] \[f(R) \equiv \Omega - \Omega_0 = \frac{v_c}{R} - \frac{v_{c, 0}}{R_0} \tag{8}\] \[f(R) \approx f(R_0) + f'(R_0) (R-R_0) \tag{9}\]のように近似すると
\[f'(R_0) = \left. \frac{df}{dR} \right|_{R=R_0} = - \frac{v_{c, 0}}{R_0^2} + \frac{1}{R_0} \left. \frac{dv_c}{dR} \right|_{R=R_0} \tag{10}\]より
\[f(R) \approx \frac{1}{R_0} \left( \left. \frac{dv_c}{dR} \right|_{R=R_0} - \frac{v_{c, 0}}{R_0}\right) (R-R_0) \tag{11}\]と求まります。 ここから、\(v_L\)は
\[v_L \approx \left( \left. \frac{dv_c}{dR} \right|_{R=R_0} - \frac{v_{c, 0}}{R_0}\right) (R-R_0) \sin \ell \tag{12}\]のように計算されます。 さらに\(d \ll R_0\)として、\(R_0 - R \approx d \cos \ell\)と近似すると
\[v_L \approx \left( \left. \frac{dv_c}{dR} \right|_{R=R_0} - \frac{v_{c, 0}}{R_0}\right) d \sin \ell \cos \ell = - \frac{1}{2} \left( \left. \frac{dv_c}{dR} \right|_{R=R_0} - \frac{v_{c, 0}}{R_0}\right) d \sin 2 \ell \tag{13}\]を得ます。 ここで
\[A \equiv \frac{1}{2} \left( \frac{v_{c, 0}}{R_0} - \left. \frac{dv_c}{dR} \right|_{R=R_0}\right) \tag{14}\]と置いておきましょう。 続いて、\(v_T\)についても計算すると
\[\begin{align} v_T &\approx \left( \left. \frac{dv_c}{dR} \right|_{R=R_0} - \frac{v_{c, 0}}{R_0}\right) (R-R_0) \cos \ell - \Omega d = - \left( \left. \frac{dv_c}{dR} \right|_{R=R_0} - \frac{v_{c, 0}}{R_0}\right) d \cos^2 \ell - \Omega d \notag \\ &= - \frac{1}{2} \left( \left. \frac{dv_c}{dR} \right|_{R=R_0} - \frac{v_{c, 0}}{R_0}\right) d (1+\cos 2\ell) - \Omega d \notag \\ &= d \left\{ - \frac{1}{2} \left( \left. \frac{dv_c}{dR} \right|_{R=R_0} - \frac{v_{c, 0}}{R_0}\right) \cos 2\ell - \frac{1}{2} \left( \left. \frac{dv_c}{dR} \right|_{R=R_0} - \frac{v_{c, 0}}{R_0}\right) - \Omega \right\} \notag \\ &= d (A \cos 2\ell + B) \tag{15} \end{align}\]のように整理されます。 途中
\[B \equiv - \left( \left. \frac{dv_c}{dR} \right|_{R=R_0} - \frac{v_{c, 0}}{R_0}\right) - \Omega \tag{16}\]のように置きました。 ここで(11)式より
\[\begin{align} &\Omega - \Omega_0 \approx \frac{1}{R_0} \left( \left. \frac{dv_c}{dR} \right|_{R=R_0} - \frac{v_{c, 0}}{R_0}\right) (R-R_0) \notag \\ &\Longrightarrow \ \Omega \approx \frac{R}{R_0} \left( \left. \frac{dv_c}{dR} \right|_{R=R_0} - \frac{v_{c, 0}}{R_0}\right) - \left. \frac{dv_c}{dR} \right|_{R=R_0} + 2\Omega_0 \tag{17} \end{align}\]を(16)式に代入すると
\[B = \left( \frac{1}{2} - \frac{R}{R_0}\right) \left( \left. \frac{dv_c}{dR} \right|_{R=R_0} - \frac{v_{c, 0}}{R_0}\right) - \frac{v_{c, 0}}{R_0} \tag{18}\]今、\(d \ll R_0\)のような太陽近傍を考えているので、\(R \sim R_0\)より
\[B = - \frac{1}{2} \left( \left. \frac{dv_c}{dR} \right|_{R=R_0} + \frac{v_{c, 0}}{R_0}\right) \tag{19}\]を得ます。 ここまでで導出された\(A, B\)をオールトの定数と呼びます。 これらは通常、\(\mathrm{km} \ \mathrm{s}^{-1} \ \mathrm{kpc}^{-1}\)の単位で表されます。
固有運動とオールト定数の決定
オールト定数を観測から決定することを考えましょう。 実際の観測では\(v_T\)ではなく、天球面上に射影された固有運動による角度の変化を見ることになります。 銀河面方向の固有運動を\(\mu_\ell\)のように書くと
\[\mu_\ell = \frac{v_T}{d} = A \cos 2 \ell + B \tag{20}\]のようになります。 実際の観測では\(v_T\)は\(\mathrm{km} \ s^{-1}\)、\(\mu_\ell\)は秒角/年、\(d\)はkpcなどの単位が用いられます。
(20)式から、横軸を\(\ell\)、縦軸を\(\mu_\ell\)のようなグラフを作ると、下図のように波打つ様子が得られます。 実データである黒点を\(\cos 2 \ell\)でフィッティングし、\(A, B\)を推定すれば、オールト定数を求めたことになります。
 (図はBovy (2017)より)
(図はBovy (2017)より)
エピサイクリック近似とオールト定数
(14), (19)式より
\[A-B = \frac{v_{c, 0}}{R_0} = \Omega_0 \tag{21}\] \[A+B = \left. \frac{dv_c}{dR} \right|_{R=R_0} \tag{22}\]のような関係にあることがわかります。 これは、先ほどのようにして観測から\(A, B\)を求めることで、天の川銀河の回転に関する情報が得られることを意味します。 ここで
\[\frac{dv_c}{dR} = \frac{d}{dR} (R \Omega) = \Omega + R \frac{d\Omega}{dR} \tag{23}\]より
\[B = - \frac{1}{2} \left( 2\Omega_0 + R_0 \left. \frac{d\Omega}{dR} \right|_{R=R_0}\right) \tag{24}\]のように書き換えることができます。 ここで\(\Omega_0\)は\(R=R_0\)での角速度です。 突然ですが、これを用いて\(R=R_0\)でのエピサイクリック振動数を書き直してみましょう。
\[\kappa_0^2 = 4\Omega_0^2 + 2R_0 \Omega_0 \left. \frac{d\Omega}{dR} \right|_{R=R_0} = -4 \Omega_0 B \tag{25}\]さらに(21)式より
\[\kappa_0^2 = 4 B (B-A) \tag{26}\]のような、オールト定数とエピサイクリック運動の関係式を導くことができました。 以降では、太陽近傍にいる恒星がエピサイクリック運動をしていると仮定しましょう。 観測から\(A\sim 15.3 \mathrm{km / s^{-1} / kpc^{-1}}, B\sim -11.9 \mathrm{km / s^{-1} / kpc^{-1}}\)より
\[\kappa_0^2 \sim 36.0^2 \mathrm{km / s^{-1} / kpc^{-1}}, \qquad \Omega_0 \sim 27.2 \mathrm{km / s^{-1} / kpc^{-1}} \ \Longrightarrow \ \frac{\kappa_0}{\Omega} \sim \frac{4}{3} \tag{27}\]を得ます。 つまり太陽近傍が銀河中心の周りを3回周回する間に、エピサイクリック運動により動径方向に4回振動を行うことを意味します。
以降ではさらに、速度分散とオールト定数の関係について見ていきましょう。 太陽近傍にいる天体の動径方向と方位角方向の速度はそれぞれ
のようになります。 太陽は\(R = R_0\)で円運動をしているとすると、太陽から見た場合の太陽近傍の天体の運動速度は
\[\Delta v_R = - X \kappa_0 \sin (\kappa_0 t + \psi) \underbrace{=}_{(26)} - X \sqrt{4B(B-A)} \sin (\kappa_0 t + \psi) \tag{30}\] \[\Delta v_\varphi = v_\varphi - R_0 \Omega_0 = R_0 (\Omega - \Omega_0) - 2 \Omega X \cos (\kappa_0 t + \psi) \tag{31}\]さらに
\[\Omega - \Omega_0 \approx \left. \frac{d\Omega}{dR} \right|_{R=R_0} \underbrace{(R-R_0)}_{=x(t)} = \left. \frac{d\Omega}{dR} \right|_{R=R_0} X \cos (\kappa_0 t+\alpha) \tag{32}\]より
\[\Delta v_\varphi \approx - \left( R_0 \left. \frac{d\Omega}{dR} \right|_{R=R_0} + 2\Omega_0 \right) X \cos (\kappa_0 t+\psi) \underbrace{=}_{(24)} -2B X \cos (\kappa_0 t + \psi) \tag{33}\]と求まります。 複数の太陽近傍天体に対する平均をとることを考えましょう。 このとき位相には相関がないとすると
\[\sigma_R^2 = \langle \Delta v_R^2 \rangle = 4BX^2 (B-A) \langle \sin^2 (\kappa t + \psi)\rangle = 2 B X^2 (B-A) \tag{34}\] \[\sigma_\varphi^2 = \langle \Delta v_\varphi^2 \rangle = 4 B^2 X^2 \langle \cos^2 (\kappa t + \psi)\rangle = 2 B^2 X^2 \tag{35}\]のようになります。 \(\langle \cdots \rangle\)は平均操作を表し、\(\langle \sin^2 (\cdots) \rangle = \langle \cos^2 (\cdots) \rangle = \frac{1}{2}\)を用いました。 以上より
\[\frac{\sigma_\varphi^2}{\sigma_R^2} = \frac{B}{B-A} \tag{36}\]のような関係を得ます。 太陽近傍の天体の速度分散\(\sigma_R, \sigma_\varphi\)を求めることができれば、(36)式を用いて\(A, B\)を算出することができます。 速度分散から天の川銀河の回転の情報を得ることができるという、強力な関係式です。 実際の\(A, B\)の値から、実際には\(\frac{\sigma_\varphi}{\sigma_R} \sim \frac{2}{3}\)と判明しています。 天の川銀河のような円盤銀河では、回転速度はflat rotationであると知られています。 その場合、\(v_c = (一定)\)です。 これより\(A = -B\)とわかるので、(36)式から\(\frac{\sigma_\varphi}{\sigma_R} = \frac{1}{\sqrt{2}}\)と求まります。 観測とflat rotationの場合の予測値が大きく外れていないことから、この理論の妥当性がわかります。
しかしこの関係式の導出には、太陽近傍の天体はエピサイクリック運動をしているという近似を用いているのでした。 よってこの関係式は、エピサイクリック近似が適用できるような、太陽近傍の非常に若い恒星集団のみに限られることに注意しましょう。
参考文献
[1] Binney & Tremaine, “Galactic Dynamics: Second Edition”
[2] Bovy, “Dyanmics and Astrophysics of Galxies”
[3] Bovy, 2017, “Galactic rotation in Gaia DR1”
[4] 祖父江義明, 有本信雄, 家正則, “銀河II”
[5] 恒星社厚生閣, “オールト定数と銀河回転 詳解”