Table of contents
磁気回転不安定性とパーカー不安定性の釣り合い
降着円盤などの差動回転円盤では、磁気回転不安定性が起こります。そのようにして強められた円盤内部の磁束は、パーカー不安定性により円盤上空に運ばれると考えられます。すると磁場を強める効果と磁場を逃して弱める効果の2つの不安定性が存在するため、これらが釣り合い、準平衡状態が実現されることが予想されます。今回はこれらの釣り合いについて考えてみましょう。
磁気回転不安定性の成長率
まずは磁気回転不安定性が起こる条件から考察します。円盤に垂直な方向に波長\(\lambda\)のアルヴェーン波が伝わっていく状況を考えます。分散関係式より、この波動が磁気張力により振動する時間スケール(あるいは波動が円盤垂直方向に伝播する時間スケール)は
\[v_A = \nu \lambda \ \Longrightarrow \ \tau_A = \frac{1}{\nu} = \frac{\lambda}{v_A}\]となります。一方、ガス円盤が1回転するのにかかる時間スケールは、円盤の角速度を\(\Omega\)とすると
\[\tau_\mathrm{rotation} = \frac{2\pi}{\Omega}\]です。磁気張力で振動するよりも高速に円盤が回転すると、それにより磁力線がたなびいて角運動量輸送が起こると考えられます。よって磁気回転不安定性の起こる条件は、大雑把に見積もると
\[\tau_\mathrm{rotation} < \tau_A \ \Longrightarrow \ \lambda > 2\pi \frac{v_A}{\Omega} \equiv \lambda_\mathrm{crit, M} \tag{1}\]のようになります。注意すべきは\(\lambda_\mathrm{crit, m} > H\)(ガス円盤のスケールハイト)のときは、この不安定性は発生しないことです。これは波長が長すぎて、逆に磁気張力がうまく角運動量を輸送できなくなるためです。 よって以下の議論では\(\lambda_\mathrm{crit, m} < H\)とします。
このこれらの条件を満たしているとき、最も成長が早い不安定性はどの波長でしょうか。その答えは単純です。
- 波長が\(\lambda_\mathrm{crit, m}\)以下では磁気張力による振動が支配的になり不安定性が起こらない
- 波長が長すぎると磁気張力が弱くなり、角運動量輸送効率が落ちる
この2つの議論から最も効率よく成長するは、不安定性が成長しかつ磁気張力が最も強く働くであろう\(\lambda_\mathrm{max, M} \simeq \lambda_\mathrm{crit, M}\)のときと考えることができます。この波長のとき、磁気回転不安定性の成長率は
\[\nu_\mathrm{MRI} \simeq \frac{v_A}{\lambda_\mathrm{max, M}} \simeq \frac{\Omega}{2\pi} \tag{2}\]実際、ケプラー回転しているガス円盤での磁気回転不安定性の成長率はおよそ\(0.75 \Omega\)で、大体のオーダーが一致しています。
パーカー不安定性の成長率
同様にパーカー不安定性の成長率についても議論しましょう。浮力と磁気張力によるパーカー不安定性の簡単な見積もりより、不安定となる波長は
\[\lambda > \lambda_\mathrm{crit, P} = 8H \sqrt{1+\beta^{-1}} \tag{3}\]です。ここで\(\beta = P / (B^2/8\pi)\)です。Low \(\beta\)(磁場が強い)極限では磁気張力が卓越し、パーカー不安定性は抑えられるはずです。またhigh \(\beta\)(磁場が弱い)極限では、磁場がしっかりしたループ構造を保つことができません。よって\(\beta\)は大き過ぎず小さ過ぎない値である必要があります。この議論から最大成長率を評価すると、ここは大雑把に
\[\lambda_\mathrm{max} \simeq 10 H \tag{4}\]程度と思っておけば良いでしょう(\(\beta^{-1/2}\)にしか依存しないので、まぁザックリとこれくらいのオーダーであるくらいの考えです)。この波長の不安定性の成長率は
\[\nu_\mathrm{PI} \simeq \frac{v_A}{\lambda_\mathrm{max, P}} \simeq \frac{v_A}{10H} \tag{5}\]例: 降着円盤での釣り合い
それでは実際に磁気回転不安定性とパーカー不安定性が釣り合い、準定常状態に落ち着いている降着円盤での\(\beta\)を求めてみましょう。そのためにまずは\(H\)を\(\Omega\)を用いて記述します。簡単のため、磁場は円盤のダイナミクスには支配的な影響を及ぼしていないとして、高さ\(H\)の位置での圧力勾配と質量\(M\)の中心天体からの重力の釣り合いを考えます。
\[\vert \nabla P \vert = \frac{GM}{R^3} H \rho \ \Longrightarrow \ \frac{P}{H} \simeq \Omega^2 H \rho \ \Longrightarrow \ H^2 \simeq \frac{1}{\Omega^2} \frac{P}{\rho} \simeq \frac{C_s^2}{\Omega^2} \tag{6}\]途中、音速\(C_s^2 = \gamma P/\rho\)を用いて整理しました。(6)式を(5)式に代入すると
\[\nu_\mathrm{PI} \simeq \frac{v_A}{C_s} \frac{\Omega}{10}\]ここで
\[\frac{v_A^2}{\Omega^2} = \frac{B^2}{4\pi \rho} \frac{\rho}{ \gamma P} = \frac{2}{\gamma} \frac{B^2/8\pi}{P} = \frac{2}{\gamma \beta}\]より
\[\nu_\mathrm{PI} \simeq \sqrt{\frac{2}{\gamma \beta}} \frac{\Omega}{10} \tag{7}\](7)=(2)式として釣り合いを考えれば
\[\sqrt{\frac{2}{\gamma \beta}} \frac{\Omega}{10} = \frac{\Omega}{2\pi} \ \Longrightarrow \ \beta = \frac{2}{\gamma} \times \left( \frac{2\pi}{10}\right)^2 \sim 0.5 \tag{8}\]のように、大体1に近い値となることがわかります。ガスと磁場との間にエネルギー等分配が成り立つときが平衡状態であるという見方からすれば、これは自然なことなのかも知れません。
大局的な降着円盤シミュレーションでは、およそ\(\beta \sim 10\)になることが知られています。これは数値的な散逸により磁場が小さくなるためと言われていますが、本当のところは良く理解されていません。
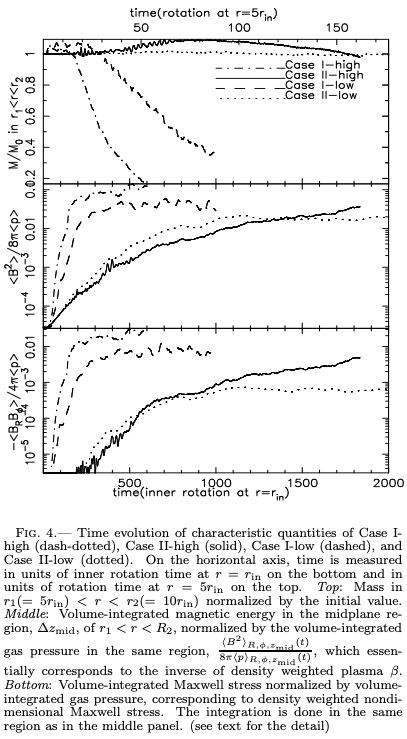
参考文献
[1] 観山 正見, 野本 憲一, 二間瀬 敏史, ”天体物理学の基礎 II”
[2] 福江純, 和田圭一, 梅村雅之, ”宇宙流体力学の基礎”
[3] S. Chandrasekhar, “Hydrodynamic and Hydromagnetic Stability”
[4] E. Priest, “Solar MagnetohydroDynamics”
[5] Suzuki & Inutsuka, 2014, “MHD Simulations of Global Accretion Disks with Vertical Magnetic Fields”