Table of contents
3次元極座標ラプラシアンの導出
概要
理系大学生ならば誰もが突き当たる(?)であろう3次元直交座標から3次元極座標へのラプラシアンの変換を、図を用いることで手軽な計算量で導出するものです。
お断り
途中、近似を用いるため、少々厳密性は欠いてしまう導出方法かもしれません。それをご理解いただいた上でこの文章をお読みいただければと思います。
復習: ラプラシアン
ラプラシアンとは、以下のような演算子です。
\[\Delta = \frac{\partial^2}{\partial x^2} +\frac{\partial^2}{\partial y^2} +\frac{\partial^2}{\partial z^2}\]上述は\((x, y, z)\)の直交座標系での表記です。そしてこの演算子の極座標での表記は以下のようになります。
\[\Delta = \frac{1}{R^2} \frac{\partial}{\partial R} \left( R^2 \frac{\partial}{\partial R}\right) + \frac{1}{R^2 \sin\theta} \frac{\partial}{\partial \theta} \left( \sin\theta \frac{\partial}{\partial \theta}\right) + \frac{1}{R^2 \sin^2\theta} \frac{\partial^2}{\partial \varphi^2}\]用意するもの
導出には以下のものを用います。
極座標での勾配の要素
\[(\nabla u)_R =\frac{\partial u}{\partial R}, \ (\nabla u)_\theta =\frac{1}{R} \frac{\partial u}{\partial \theta}, \ (\nabla u)_\varphi = \frac{1}{R\sin \theta} \frac{\partial u}{\partial \varphi}\]ガウスの定理
\[\iiint \nabla \cdot (\nabla u) dV = \iint (\nabla u)\cdot d {\bf S}\]\((R, \theta, \varphi)\)での微小体積要素
3次元極座標系における微小体積要素は下図を用いて、以下のように求まります。
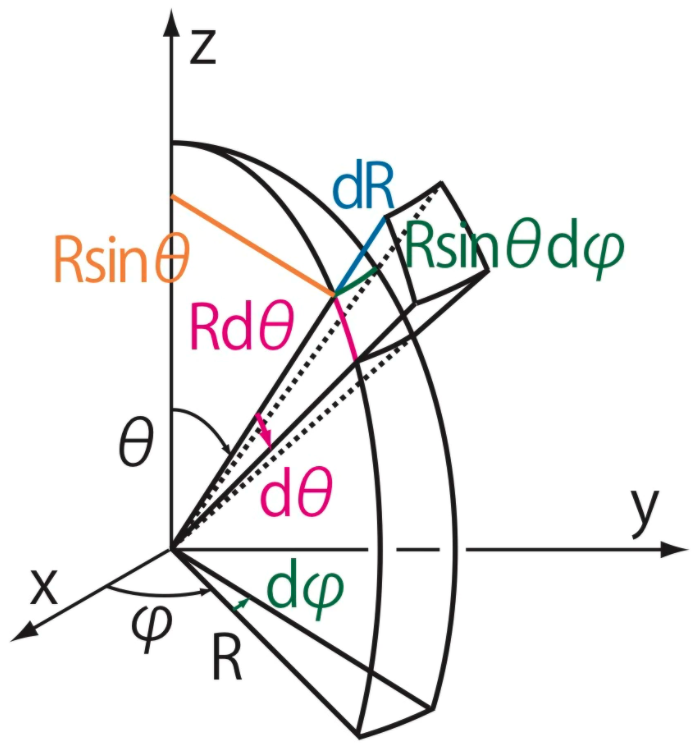
それでは導出を見ていきましょう。
導出
ガウスの定理の左辺と、微小体積での積分より
\[\iiint \Delta u dV \simeq (\Delta u) R^2 \sin \theta dR d\theta d\varphi\]ガウスの定理の右辺と、勾配の各成分の計算を行います。微小面積での面積分より
\[\iint (\nabla u) \cdot d{\bf S} \simeq \left[ \frac{\partial u}{\partial R} R^2 \sin \theta d\theta d\varphi \right]_R^{R+dR} + \left[ \frac{1}{R} \frac{\partial u}{\partial \theta} R \sin \theta dR d \varphi \right]_\theta^{\theta+d\theta} + \left[ \frac{1}{R \sin \theta} \frac{\partial u}{\partial \varphi} R dR d\theta \right]_\varphi^{\varphi+d\varphi}\]微分の定義より
\[\left[ \frac{\partial u}{\partial R} R^2 \sin \theta d\theta d\varphi \right]_R^{R+dR} \simeq \frac{\partial }{\partial R} \left( R^2 \frac{\partial u}{\partial R} \right) dR \sin \theta d\theta d\varphi = \frac{1}{R^2} \frac{\partial }{\partial R} \left( R^2 \frac{\partial u}{\partial R} \right) R^2 \sin \theta dR d\theta d\varphi\] \[\left[ \frac{1}{R} \frac{\partial u}{\partial \theta} R \sin \theta dR d \varphi \right]_\theta^{\theta+d\theta} \simeq \frac{\partial}{\partial \theta} \left( \sin \theta \frac{\partial u}{\partial \theta}\right) d\theta dR d\varphi = \frac{1}{R^2 \sin \theta}\frac{\partial}{\partial \theta} \left( \sin \theta \frac{\partial u}{\partial \theta}\right) R^2 \sin \theta dR d\theta d\varphi\] \[\left[ \frac{1}{R \sin \theta} \frac{\partial u}{\partial \varphi} R dR d\theta \right]_\varphi^{\varphi+d\varphi} \simeq \frac{1}{\sin \theta} \frac{\partial^2 u}{\partial \varphi^2} d\varphi dR d\theta =\frac{1}{R^2 \sin^2 \theta} \frac{\partial^2 u}{\partial \varphi^2} R^2 \sin \theta dR d\theta d\varphi\]よって
\[\Delta u= \frac{1}{R^2} \frac{\partial}{\partial R} \left( R^2 \frac{\partial u}{\partial R}\right) + \frac{1}{R^2 \sin\theta} \frac{\partial}{\partial \theta} \left( \sin\theta \frac{\partial u}{\partial \theta}\right) + \frac{1}{R^2 \sin^2\theta} \frac{\partial^2 u}{\partial \varphi^2}\]と求まります。
結言
微小体積要素と微小面積要素を用いることにより、導出を簡単化するというトリックを用いた導出をご紹介しました。