Table of contents
遅延グリーン関数
ダランベレシアンとグリーン関数
関数\(\phi\)が\(\Box \phi = -4\pi \rho_e (\mathbf{r}, t)\)を満たすとします。ここで\(\Box\)はダランベレシアン(D’Alambertian, ダランベール演算子)で
\[\Box \equiv \nabla^2 - \frac{1}{c^2} \frac{\partial^2}{\partial t^2} \tag{1}\]です。このとき
\[\Box G (\mathbf{r}, t) = -\delta^3 (\mathbf{r}) \delta (t) \tag{2}\]を満たすグリーン関数\(G\)を用いて、ポテンシャル\(\phi\)を表現しましょう。(2)式の両辺に\(\rho_e (\mathbf{r}', t')\)をかけたものを両辺\(\mathbf{r}', t'\)で積分すると
\[\begin{align} &\rho_e (\mathbf{r}', t') \Box G(\mathbf{r}-\mathbf{r}', t-t') = - \rho_e(\mathbf{r}', t') \delta^3(\mathbf{r}-\mathbf{r}') \delta(t-t') \notag \\ &\Longrightarrow \ 4\pi \iiint d\mathbf{r'} \int dt' \rho_e(\mathbf{r}', t') \Box G(\mathbf{r}-\mathbf{r}', t-t') = -4\pi \iiint d\mathbf{r}' \int dt' \rho_e(\mathbf{r}' ,t') \delta^3(\mathbf{r}-\mathbf{r}') \delta(t-t') \notag \\ & \qquad = -4\pi \rho_e(\mathbf{r}, t) = \Box \phi(\mathbf{r}, t) \notag \end{align}\]一方、\(\Box\)は\(\mathbf{r}, t\)に作用する演算子なので
\[4\pi \iiint d\mathbf{r'} \int dt' \rho_e(\mathbf{r}', t') \Box G(\mathbf{r}-\mathbf{r}', t-t') = \Box \left( 4\pi \iiint d\mathbf{r}' \int dt' G(\mathbf{r}-\mathbf{r}', t-t') \rho_e(\mathbf{r}', t') \right)\]となります。以上より
\[\phi (\mathbf{r}, t) = 4\pi \iiint d\mathbf{r'} \int dt' G(\mathbf{r}-\mathbf{r}', t-t') \rho_e(\mathbf{r}', t') \tag{3}\]と表されることがわかります。
遅延グリーン関数 (Retarded Green function)
次の方程式
\[\Box G (\mathbf{r}, t) = - \delta^3 (\mathbf{r}) \delta(t) \tag{4}\]を満たすグリーン関数のうち
\[G(\mathbf{r}, t) \left\{ \begin{array}{cc} \neq 0 & t \geq 0 \\ = 0 & t < 0 \end{array} \right.\]を満たすものを遅延グリーン関数(Retarded Green function)と呼びます。遅延グリーン関数を次の手順にしたがって求めましょう。
フーリエ変換
グリーン関数のフーリエ積分表示(フーリエ逆変換)は
\[G(\mathbf{r}, t) = \int_{-\infty}^{\infty} d\omega \iiint_{-\infty}^\infty d^3 \mathbf{k} \ \hat{G} (\mathbf{k}, \omega) e^{-i \omega t + i \mathbf{k} \cdot \mathbf{r}} \tag{5}\]そしてデルタ関数のフーリエ積分表示は
\[\delta^3(\mathbf{r}) \delta(t) = \frac{1}{(2\pi)^4}\int_{-\infty}^{\infty} d\omega \iiint_{-\infty}^\infty d^3 \mathbf{k} \ e^{-i \omega t + i \mathbf{k} \cdot \mathbf{r}} \tag{6}\]です。これらを(4)式に代入します。
\[\begin{align} \Box G(\mathbf{r}, t) &= \left(\nabla^2 - \frac{1}{c^2} \frac{\partial^2}{\partial t^2} \right)\int_{-\infty}^\infty d\omega \iiint_{-\infty}^\infty d^3 \mathbf{k} {\hat G}(\mathbf{k}, \omega) e^{-i\omega t+ i\mathbf{k}\cdot \mathbf{r}} \notag \\ &= \int_{-\infty}^\infty d\omega \iiint_{-\infty}^\infty d^3 \mathbf{k} {\hat G}(\mathbf{k}, \omega) \left( \nabla^2-\frac{1}{c^2} \frac{\partial^2}{\partial t^2} \right) e^{-i\omega t+ i\mathbf{k}\cdot \mathbf{r}} \notag \\ &= \int_{-\infty}^\infty d\omega \iiint_{-\infty}^\infty d^3 \mathbf{k} {\hat G}(\mathbf{k}, \omega) \left( i^2 \left| \mathbf{k}\right|^2 -\frac{1}{c^2} (-i \omega)^2 \right) e^{-i\omega t+ i \mathbf{k}\cdot \mathbf{r}} \notag \\ &= \int_{-\infty}^\infty d\omega \iiint_{-\infty}^\infty d^3 \mathbf{k} {\hat G}(\mathbf{k}, \omega) \left( - \left| \mathbf{k}\right|^2 + \frac{\omega^2}{c^2}\right) e^{-i\omega t+ i \mathbf{k}\cdot \mathbf{r}} \notag \\ &= - \frac{1}{(2\pi)^4}\int_{-\infty}^\infty d\omega \iiint_{-\infty}^\infty d^3 \mathbf{k} \ e^{-i\omega t+ i \mathbf{k}\cdot \mathbf{r}} \notag \end{align}\]よって
\[{\hat G} (\mathbf{k}, \omega) = - \frac{1}{(2\pi)^4} \frac{1}{-k^2 + \frac{\omega^2}{c^2}} = -\frac{c^2}{(2\pi)^4} \frac{1}{\omega^2 - c^2 k^2} \tag{7}\]となります。
逆フーリエ変換
(7)式を逆フーリエ変換して、遅延グリーン関数を求めましょう。
\[G(\mathbf{r},t) = -\frac{c^2}{(2\pi)^4}\int_{-\infty}^\infty d\omega \iiint_{-\infty}^\infty d^3\mathbf{k} \ \frac{e^{-i\omega t+ i\mathbf{k}\cdot \mathbf{r}}}{\omega^2 - c^2 k^2} = -\frac{c^2}{(2\pi)^4} \iiint_{-\infty}^\infty d^3\mathbf{k} e^{i\mathbf{k}\cdot \mathbf{r}}\int_{-\infty}^\infty d\omega\frac{e^{-i\omega t}}{\omega^2 - c^2 k^2}\]この式の\(\omega\)での積分を実行するために、\(f(z) = \frac{e^{-izt}}{z^2 - c^2 k^2}\)の積分を以下のような複素数平面上の閉曲路で考えます(\(z = \omega + i \Omega\))。下図のように極を上に避けるように経路を選択することで、遅延グリーン関数の条件を満たすことができます。
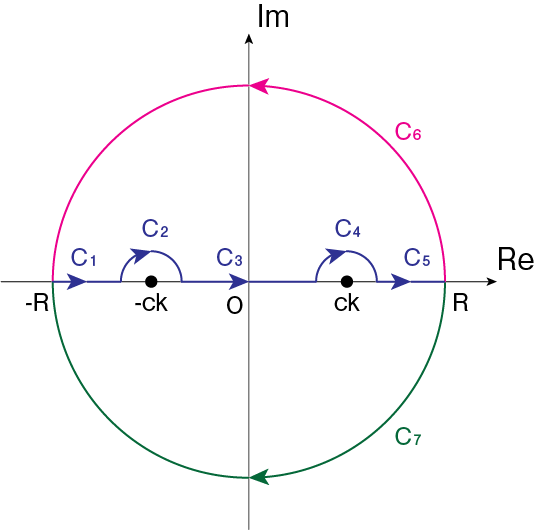
(i) \(t < 0\)の計算
コーシーの積分定理より
\[\oint_{C_1+C_2+C_3+C_4+C_5+C_6} dz \ f(z) = \int_{C_1+C_2+C_3+C_4+C_5} dz f(z) + \int_{C_6} dz \ f(z) = 0\]\(C_6 : z = Re^{i\theta} \ (\theta: 0 \rightarrow \pi)\)において、\(dz = i R e^{i\theta} d\theta\)より
\[\int_{C_6} dz \ f(z) = \int_0^\pi d\theta \frac{iRe^{i\theta}}{R^2e^{2i\theta}-c^2k^2} e^{-itRe^{i\theta}} = iR \int_0^\pi d\theta \frac{e^{i\theta}}{R^2e^{2i\theta}-c^2k^2} e^{-itR\cos \theta}e^{tR\sin \theta}\]この積分の大きさは絶対値をとることで評価できます。
\[\begin{align} \left| \int_{C_6} dz \ f(z) \right| &= \left| iR \int_0^\pi d\theta \frac{e^{i\theta}}{R^2e^{2i\theta}-c^2k^2} e^{-itR\cos \theta}e^{tR\sin \theta}\right| \notag \\ &\leq R \int_0^\pi d\theta \left| \frac{e^{i\theta}}{R^2e^{2i\theta}-c^2k^2} \right| \left| e^{-itR\cos \theta} \right| \left| e^{tR\sin \theta} \right| \notag \\ &\leq R \int_{0}^\pi d\theta \frac{e^{tR\sin \theta}}{R^2 -c^2 k^2} \ (\because \ \left| e^{i\theta} \right| =1, \left| R^2 e^{2i\theta} -c^2k^2\right| \geq R^2-c^2k^2) \notag \end{align}\]\(0 \leq \theta \leq \pi\)において\(\sin \theta > 0\)より、\(t < 0\)であれば\(\int_{C_6} dz \ f(z) \rightarrow 0\)となります。よって
\[\lim_{R \rightarrow \infty, r \rightarrow 0} \int_{C_1+ C_2 + C_3 + C_4 + C_5 + C_6} dz \ f(z) = \int_{-\infty}^\infty d\omega \frac{e^{-i\omega t}}{\omega^2 - c^2 k^2} = 0 \ (t<0) \tag{8}\](ii) \(t \geq 0\)の計算
留数定理より
\[\oint_{C_1+C_2+C_3+C_4+C_5+C_7} dz \ f(z) = -2\pi i\left\{ {\rm Res}(f, -ck)+ {\rm Res}(f, ck)\right\}\]ここで\(\mathrm{Res} (f, a)\)は関数\(f\)の\(a\)に対する留数を意味します。また右辺のマイナス符号は積分が時計回りであることから現れたものです。留数を計算するために以下のように変形します。
\[f(z) = \frac{e^{-izt}}{z^2 - c^2k^2} = \frac{1}{2ck} \left( \frac{1}{z-ck} -\frac{1}{z+ck} \right)e^{-izt}\]そして\(e^{-izt}\)を\(z = ck, -ck\)の周りでテイラー展開をしたもの
\[e^{-izt} = \left. \sum_{n=0}^\infty \frac{1}{n!} \frac{d^n}{dz^n} e^{-izt} \right|_{z=ck} (z-ck)^n = e^{-ickt} + (-it) e^{-ickt} (z-ck) + \frac{(-it)^2}{2} e^{-ickt} (z-ck)^2 + \cdots\] \[e^{-izt} = \left. \sum_{n=0}^\infty \frac{1}{n!} \frac{d^n}{dz^n} e^{-izt} \right|_{z=-ck} (z+ck)^n = e^{ickt} + (-it) e^{ickt} (z+ck) + \frac{(-it)^2}{2} e^{ickt} (z+ck)^2 + \cdots\]を代入すると
\[f(z) = \frac{1}{2ck} \left\{ \left(\frac{e^{-ickt}}{z-ck} + (-it) e^{-ickt} + \frac{(-it)^2}{2} e^{-ickt} (z-ck) + \cdots \right) - \left(\frac{e^{ickt}}{z+ck} + (-it) e^{ickt} + \frac{(-it)^2}{2} e^{ickt} (z+ck) + \cdots \right) \right\}\]\(z = ck\)で正則でないのは\(\frac{1}{2ck} \frac{e^{-ickt}}{z-ck}\)の項のみ、そして\(z = -ck\)で正則でないのは\(- \frac{1}{2ck} \frac{e^{ickt}}{z+ck}\)の項のみです。よって
\[\int_{C_1+ C_2 + C_3 + C_4 + C_5 } dz \ f(z) + \int_{C_7} dz \ f(z) = -\frac{\pi i}{ck}\left( - e^{ickt} + e^{-ickt}\right)\]\(r \rightarrow 0, R \rightarrow \infty\)として
\[\int_{-\infty}^\infty d\omega \ f(\omega) = -\lim_{R \rightarrow \infty} \int_{C_7} dz \ f(z) - \frac{\pi i}{ck} \left( - e^{ickt} + e^{-ickt}\right)\]上式での\(C_7\)上での積分は先ほどの\(C_6\)上での積分区間を\(\theta : 0 \rightarrow - \pi\)にしたものに等しいので
\[\int_{C_7} dz \ f(z) = \int_0^{- \pi} d\theta \frac{iRe^{i\theta}}{R^2e^{2i\theta}-c^2k^2} e^{-itRe^{i\theta}} =iR \int_0^\pi d\theta \frac{e^{i\theta}}{R^2e^{2i\theta}-c^2k^2} e^{-itR\cos \theta}e^{tR\sin \theta}\]先ほどと同様に両辺の絶対値をとって、積分値の大きさを評価しましょう。
\[\begin{align} \left| \int_{C_7} dz f(z) \right| &= \left| iR \int_0^{-\pi} d\theta \frac{e^{i\theta}}{R^2e^{2i\theta}-c^2k^2} e^{-itR\cos \theta}e^{tR\sin \theta}\right| \notag \\ &\leq R \int_0^{- \pi} d\theta \left| \frac{e^{i\theta}}{R^2e^{2i\theta}-c^2k^2} \right| \left| e^{-itR\cos \theta} \right| \left| e^{tR\sin \theta} \right| \notag \\ &\leq R \int_{0}^{- \pi} d\theta \frac{e^{tR\sin \theta}}{R^2 -c^2 k^2} \ (\because \ \left| e^{i\theta} \right| =1, \left| R^2 e^{2i\theta} -c^2k^2\right| \geq R^2-c^2k^2) \notag \end{align}\]\(-\pi < \theta < 0\)では\(\sin \theta < 0\)より、\(t > 0\)であれば\(\int_{C_7} dz \ f(z) \rightarrow 0\)となります。よって
\[\int_{-\infty}^\infty d\omega \frac{e^{-i\omega t}}{\omega^2 -c^2 k^2} = -\frac{\pi i}{ck}\left( -e^{ickt}+e^{-ickt}\right) = -\frac{2\pi}{ck}\sin ckt \ (t>0) \tag{9}\]となります。
(i), (ii)を合わせて…
以上を総合して
\[G(\mathbf{r}, t) = \left\{ \begin{array}{lll} \displaystyle{\frac{c}{(2\pi)^3} \iiint_{-\infty}^\infty d^3 \mathbf{k} \frac{e^{i \mathbf{k} \cdot \mathbf{r}} \sin ckt}{k} } & (t>0) \\ 0 &(t<0) \end{array} \right. \tag{10}\]となります。
積分実行
残りの\(\mathbf{k}\)空間での積分を行いましょう。そのためには積分が\(\mathbf{k}\)空間の無限大領域に渡り、かつ計算が簡単になるような座標を設定します。すると下図のように、\(\mathbf{r}\)を\(k_z\)に一致させる座標設定を取ると良いでしょう。
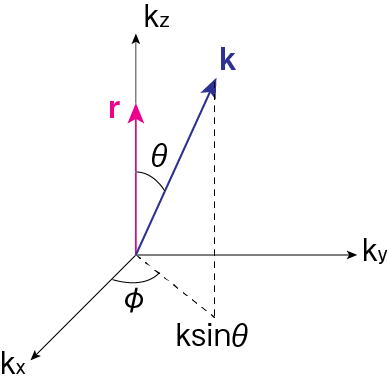
\(t > 0, r>0\)より\(\delta (t+r/c) = 0\)です。よって
\[G(\mathbf{r}, t) = \left\{ \begin{array}{ll} \displaystyle {\frac{1}{4\pi} \frac{\delta(t-\frac{r}{c})}{r}} & (t>0)\\ 0 & (t<0) \end{array} \right. \tag{11}\]と求まります。
極の避け方について(避け方が問題になるときとならないとき)
以下のsinc関数の積分計算
\[\int_{-\infty}^\infty \frac{\sin x}{x} dx = \pi\]を行うときには\(e^{ix}/x, e^{-ix}/x\)のそれぞれの積分の主値を足し合わせたものとして計算され、\(x = 0\)をどのように避けるかは議論する必要がありませんでした。その理由は
\[\lim_{x \rightarrow 0} \frac{\sin x}{x} = 1\]なので、実は\(x = 0\)は極ではないためです。しかし、計算の便宜上
\[\frac{\sin x}{x} = \frac{1}{2i} \left( \frac{e^{ix}}{x} - \frac{e^{-ix}}{x} \right)\]のように変形していたため、極があるように見えていただけなのでした。\(\sin x/ x\)の積分計算は、実際にはコーシーの主値の表記\(P\)を用いて
\[P \int_{-\infty}^\infty dx \frac{\sin x}{x} = \lim_{\epsilon \rightarrow 0}\left( \int_{-\infty}^{-\epsilon} dx \frac{\sin x}{x} + \int_{\epsilon}^\infty dx \frac{\sin x}{x}\right) = \int_{-\infty}^{\infty} dx \frac{\sin x}{x}\]のように書けます。特異点を半円で避けその半径の0極限を取る場合、いくら積分経路を0に持っていっても、特異点では無限大に関数の値が発散しているため、積分の値は有限となります。しかし、この積分は\(x = 0\)で有限の値かつ連続なので、経路の避け方を議論する必要なく積分が行えたのです。
参考文献
[1] Rybicki & Lightman, “Radiative Processes in Astrophysics”
[2] 観山正見, 二間瀬敏史, 野本憲一, ”天体物理学の基礎 II”
[3] 寺沢寛一, “自然科学者のための数学概論”