Table of contents
\(\beta\)関数
ベータ関数はアドリアン・マリ・ルジャンドルが用いたのが始まりですが、その名前自体は1990にウィッタカーとワトソンによって命名されました。
定義
\[B(x, y) = \int_0^1 t^{x-1} (1-t)^{y-1} dt \tag{1}\]上の式において\(t=\sin^2 \theta\)と置換すると、\(dt = 2 \sin \theta \cos \theta d\theta\)より
\[B(x, y) = \int_0^{\pi/2} \sin^{2x-2} \theta (1-\sin^2 \theta)^{y-1} 2\sin \theta \cos \theta d\theta = 2\int_0^{\pi/2} \sin^{2x-1} \theta \cos^{2y-1} \theta d\theta \tag{2}\]とも書けます。
ガンマ関数との関係式
\[\Gamma (x) \Gamma (y) = \int_0^\infty e^{-t} t^{x-1} dt \int_0^\infty e^{-s} s^{y-1} ds\]\(t=T^2, s=S^2\)と置換すると
\[\Gamma(x) \Gamma (y) = \int_0^\infty e^{-T^2} t^{2x-2} 2T dt \int_0^\infty e^{-S^2} s^{2y-2} 2S dS = 4 \int_0^\infty e^{-T^2} T^{2x-1} dT \int_0^\infty e^{-S^2} S^{2y-1} dS\]これを\(TS\)の2次元平面上の積分と考え、積分を極座標に直しましょう。すなわち\(T=r\cos\theta, S=r\sin \theta\)のようにして、積分範囲を\(r: 0 \rightarrow \infty, \theta : 0\rightarrow \pi/2\)とします。このとき\(dT dS = r drd\theta\)となります。以上より
\[\begin{aligned} \Gamma (x) \Gamma(y) &= \overbrace{2 \int_0^\infty e^{-r^2} r^{2x+2y-1} dr}^{R=r^2と置換} \underbrace{2 \int_0^{\pi/2} \sin^{2x-1} \theta \cos^{2y-1} \theta d\theta}_{(2)} = \underbrace{\int_0^\infty e^{-R} R^{(x+y)-1} dR}_{ガンマ関数の定義より} B(x, y) \\ &= \Gamma(x+y) B(x, y) \end{aligned}\] \[\therefore \ B(x, y) = \frac{\Gamma(x) \Gamma(y)}{\Gamma(x+y)} = B(y, x) \tag{3}\]ベータ関数から導ける公式
(3)式に\(x=z, y=1-z\)を代入すると
\[\frac{\Gamma(z) \Gamma(1-z)}{\Gamma(z+1-z)} = B(z, 1-z) = \int_0^1 t^{z-1} (1-t)^{-z} dt\]\(u=t(1-t)^{-1}\)と置換すると\(dt=du/(1+u)^2\)より
\[\Gamma(z) \Gamma(1-z) = \int_0^\infty \frac{1+u}{u}u^{z} \frac{du}{(1+u)^2} = \int_0^\infty \frac{u^{z-1}}{1+u} du\]この積分値を求めるために\(f(v) = \frac{v^{z-1}}{1-v}\)を、複素数平面上の下図のような経路で積分することを考えます。
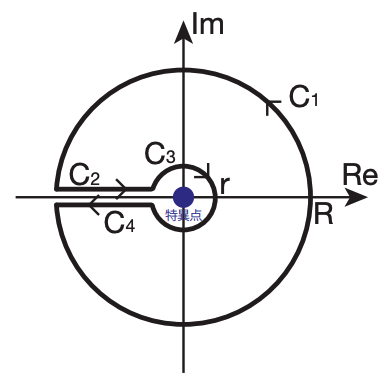
\(0 \lt z \lt 1\)のとき\(v=0\)が特異点になります。そしてこの点における留数は\(\mathrm{Res} (v^{z-1}/(1-v)) = 1\)です。留数定理より
\[\oint_{C_1+C_2+C_3+C_4} f(v) dv = -2\pi i\]時計回りに特異点を周回しているので、右辺にマイナスがついていることに注意しましょう。
\[\int_{C_1} \frac{v^{z-1}}{1-v} dv \underbrace{=}_{v\rightarrow Re^{i\theta}} \int_{-\pi}^\pi \frac{(Re^{i\theta})^{z-1}}{1-Re^{i\theta}} Re^{i\theta} d\theta \underbrace{\Longrightarrow}_{R\rightarrow \infty} 0\] \[\int_{C_2} \frac{v^{z-1}}{1-v} dv = \int_{-R}^{-r} \frac{v^{z-1}}{1-v} dv \underbrace{=}_{v=-u=ue^{i\pi}} \int_r^R \frac{u^{z-1}}{1+u} e^{i(z-1)\pi} du\] \[\int_{C_3} \frac{v^{z-1}}{1-v} dv \underbrace{=}_{v\rightarrow re^{i\theta}} \int_{-\pi}^\pi \frac{(re^{i\theta})^{z-1}}{1-re^{i\theta}} r e^{i\theta} d\theta \underbrace{\Longrightarrow}_{r\rightarrow 0} 0\] \[\int_{C_4} \frac{v^{z-1}}{1-v} dv = \int_{-r}^{-R} \frac{v^{z-1}}{1-v} dv \underbrace{=}_{v=-u=ue^{-i\pi}} \int_r^R \frac{u^{z-1}}{1+u} e^{-iz\pi} du\] \[\begin{aligned} \therefore \ -2\pi i &= \oint_{C_1+C_2+C_3+C_4} f(v) dv \underbrace{=}_{r\rightarrow 0, R \rightarrow \infty} \int_0^\infty \frac{u^{z-1}}{1+u} du (e^{i(z-1)\pi} + e^{-iz\pi}) \\ &= (-e^{iz\pi} + e^{-iz\pi}) \int_0^\infty \frac{u^{z-1}}{1+u} du = -2i \sin(z\pi) \int_0^\infty \frac{u^{z-1}}{1+u} du = -2i \sin(z\pi) \Gamma(z) \Gamma(1-z) \end{aligned}\]よって
\[\Gamma(z) \Gamma(1-z) = \frac{\pi}{\sin(z \pi)} \tag{4}\]\(\sin^n\)の定積分公式
(2), (3)式より
\[\int_0^{\pi/2} \sin^{2x-1} \theta \cos^{2y-1} \theta d\theta = \frac{1}{2} \frac{\Gamma(x) \Gamma(y)}{\Gamma(x+y)} \tag{5}\]これに\(x=(n+1)/2, y=1/2\)を代入すると
\[\int_0^{\pi/2} \sin^n \theta d\theta = \frac{1}{2} \frac{\Gamma((n+1)/2) \Gamma(1/2)}{\Gamma(n/2+1)} = \frac{\sqrt{\pi}}{2} \frac{\Gamma((n+1)/2)}{\Gamma(n/2+1)} \tag{6}\]となります。さらに
\[\begin{aligned} \int_0^{\pi} \sin^n \theta d\theta &= \frac{\sqrt{\pi}}{2} \frac{\Gamma((n+1)/2)}{\Gamma(n/2+1)} + \underbrace{\int_{\pi/2}^\pi \sin^n \theta d\theta}_{\Theta = \theta -\pi/2と置換} = \frac{\sqrt{\pi}}{2} \frac{\Gamma((n+1)/2)}{\Gamma(n/2+1)} + \int_{0}^{\pi/2} \sin^n (\Theta + \pi/2) d\Theta \\ &= \frac{\sqrt{\pi}}{2} \frac{\Gamma((n+1)/2)}{\Gamma(n/2+1)} + \int_{0}^{\pi/2} \cos^n \Theta d\Theta \end{aligned}\](5)式に今度は\(x=1/2, y=(n+1)/2\)を代入すれば\(\cos^n\)の積分結果が求まります。結果は(6)式と同じとなることがわかります。
\[\therefore \ \int_0^\pi \sin^n \theta d\theta = \sqrt{\pi} \frac{\Gamma((n+1)/2)}{\Gamma(n/2+1)} \tag{7}\]と求まります。この式はシンクロトロン放射強度を求めるときなどに使う公式です。導出方法はともかくとして、電波天文学や磁場に関わる天体物理現象を扱う方々はぜひ覚えておきましょう。
参考文献
- 数理系のための基礎と応用 微分積分II -理論を中心に-, 金子
- 解析入門I, 杉浦
- 物理数学, 高橋
- 物理数学I, 福山, 小形
- Wolfram MathWorld