Table of contents
半整数次のベッセル関数
ここではベッセル関数\(J_n (z) \ (n \in \mathbb{Z})\)をより一般化し、\(n = \nu = \{\pm \frac{1}{2}, \pm \frac{3}{2}, \dots\}\)のように、半整数次のベッセル関数について成り立つ式をメモします。
ベッセルの漸化式とポアソン積分表示からの変形
\[J_\nu = \frac{1}{\sqrt{\pi} \Gamma(\nu + 1/2)} \left( \frac{z}{2}\right)^\nu \int_{-1}^1 (1-\xi^2)^{\nu-1/2} e^{iz\xi} d\xi \tag{1}\]です。これは階乗を一般化したガンマ関数を用いて書かれているため、半整数次の場合にも適用できます。そしてこれは当然、ベッセル関数の満たす漸化式を満たします。よって
\[J_{\nu-1} - J_{\nu+1} = 2J_\nu', \quad J_{\nu-1} + J_{\nu+1} = \frac{2\nu}{z} J_\nu \ \Longrightarrow \ J_{\nu+1} = -J_\nu' +\frac{\nu}{z} J_\nu\]両辺に\(z^{-(\nu+1)}\)をかけて整理すると
\[z^{-(\nu+1)} J_{\nu+1} = - z^{-(\nu+1)} J_\nu' + \nu z^{-(\nu+2)} J_\nu = - \frac{1}{z} \frac{d}{dz} \left( z^{-\nu} J_\nu \right) \tag{2}\](2)式で\(\nu \rightarrow \nu+1\)とすると
\[z^{-(\nu+2)} J_{\nu+2} = - z^{-(\nu+2)} J_{\nu+1}' +(\nu + 1) z^{-(\nu+3)} J_{\nu+1} = - \frac{1}{z} \frac{d}{dz} (z^{-(z+1)} J_{\nu+1}) \underbrace{=}_{(2)} (-1)^2 \left( \frac{1}{z} \frac{d}{dz}\right)^2 (z^{-\nu} J_\nu)\]のようになります。よってこの操作を\(\xi -1\)回繰り返すと
\[z^{-(\nu+\xi)} J_{\nu+\xi} = (-1)^\xi \left( \frac{1}{z} \frac{d}{dz}\right)^\xi (z^{-\nu} J_\nu)\]を得ます。\(\xi = n, \nu = 1/2\)を代入すれば、半整数次に対するベッセル関数の式
\[z^{-(n+1/2)} J_{n+1/2} = (-1)^n \left( \frac{1}{z} \frac{d}{dz}\right)^n (z^{-1/2} J_{1/2}) \tag{3}\](1)式で\(\nu = 1/2\)としたものから
\[J_{1/2} = \frac{1}{\sqrt{\pi} \Gamma(1)} \left( \frac{z}{2} \right) \int_{-1}^1 e^{iz\xi} d\xi = \sqrt{\frac{z}{2\pi}} \frac{1}{iz} \left[ e^{iz\xi} \right]_{-1}^1 = \sqrt{\frac{2}{\pi z}} \sin z \tag{4}\]となるので、これを(3)式に代入すると
\[J_{n+1/2} (z) = (-1)^n \sqrt{\frac{2}{\pi}} z^{n+1/2} \left( \frac{1}{z} \frac{d}{dz}\right)^n \frac{\sin z}{z} \tag{5}\]となります。しかし、ここまで\(n\)は0以上の整数の場合しか考えていないため、\(\nu = n+\frac{1}{2} = \frac{1}{2}, \frac{3}{2}, \dots\)しか表現できていません。 よって次は\(-n-1/2\)のベッセル関数を表現することを考えましょう。再びベッセル関数の満たすの漸化式より
\[J_{-\nu-1} - J_{-\nu+1} = 2J_{-\nu}', \quad J_{-\nu -1} + J_{-\nu+1} = \frac{2(-\nu)}{z} J_{-\nu} \ \Longrightarrow \ J_{-\nu-1} = J_{-\nu}' - \frac{\nu}{z} J_{-\nu} \tag{6}\]この両辺に\(z^{-\nu-1}\)をかけて整理すると
\[z^{-\nu-1} J_{-\nu-1} = z^{-\nu-1} J_{-\nu}' - \nu z^{-\nu-2} J_{-\nu} = \frac{1}{z} \frac{d}{dz} (z^{-\nu} J_{-\nu}) \tag{7}\](7)式で\(\nu \rightarrow \nu+1\)とすると
\[z^{-\nu-1-1} J_{-\nu-1-1} = \frac{1}{z} \frac{d}{dz} (z^{-\nu-1} J_{-\nu-1}) \underbrace{=}_{(5)} \left( \frac{1}{z} \frac{d}{dz} \right)^2 (z^{-\nu} J_{-\nu})\]よってこの操作を\(\xi-1\)回繰り返すと
\[z^{-\nu-(\xi-1)-1} J_{-\nu-(\xi-1)-1} = z^{-\nu-\xi} J_{-\nu-\xi} = \left( \frac{1}{z} \frac{d}{dz}\right)^\xi (z^{-\nu} J_{-\nu})\]ここで\(\nu = 1/2, \xi = n\)とすれば
\[z^{-n - 1/2} J_{-n-1/2} = \left(\frac{1}{z} \frac{d}{dz} \right)^n (z^{-1/2} J_{-1/2}) \tag{8}\](6)式において\(\nu = -\frac{1}{2}\)とすると
\[J_{-1/2} = J_{1/2}' + \frac{1/2}{z} J_{1/2} \underbrace{=}_{(4)} \sqrt{\frac{2}{\pi}} \left( - \frac{z^{-3/2}}{2} \sin z + z^{-1/2} \cos z\right) + \sqrt{\frac{1}{2\pi z^3}} \sin z = \sqrt{\frac{2}{\pi z}} \cos z \tag{9}\](8), (9)式より
\[J_{-n-1/2} (z) = \sqrt{\frac{2}{\pi}} z^{n+1/2} \left( \frac{1}{z} \frac{d}{dz}\right)^n \frac{\cos z}{z} \tag{10}\]可視化
半整数次のベッセル関数を図示すると以下のようになります。
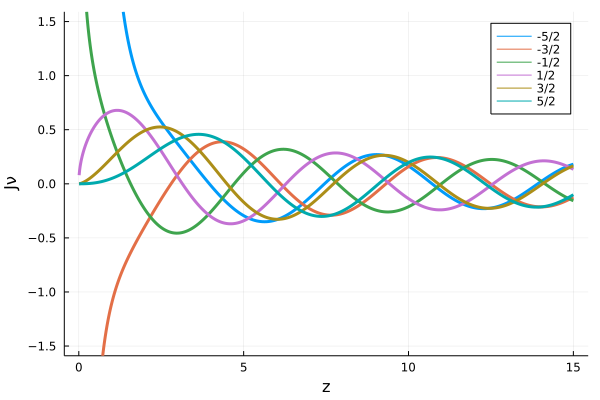
半整数次の中でも\(\frac{1}{2}, \frac{3}{2}, \frac{5}{2}, \dots\)は正の整数次のベッセル関数と同じような振る舞いをしますが、\(-\frac{1}{2}, -\frac{3}{2}, - \frac{5}{2}, \dots\)のようにマイナスの半整数次のものは\(z=0\)で無限大に発散することがわかります。
また、可視化に用いたJuliaソースコードも以下に示します。先述の通り\(z=0\)で無限大に発散する関数があるので、図示する際には0.01などの小さな数値から範囲を出発させると良いでしょう。
using Plots
using SpecialFunctions
# set x coordinate
xmax = 15.0
xmin = 0.01
nx = 1000
xs = range(xmin, xmax, length=nx)
# initialize plot
p = plot()
# get half bessel function
ys = besselj.(-5/2, xs)
plot!(xs, ys, xlim=[xmin, xmax], ylim=[-1.5, 1.5], linewidth=3, label="-5/2", legend=:topright, xlabel="z", ylabel="Jν", )
# get half bessel function
ys = besselj.(-3/2, xs)
plot!(xs, ys, xlim=[xmin, xmax], linewidth=3, label="-3/2")
# get half bessel function
ys = besselj.(-1/2, xs)
plot!(xs, ys, xlim=[xmin, xmax], linewidth=3, label="-1/2")
# get half bessel function
ys = besselj.(1/2, xs)
plot!(xs, ys, xlim=[xmin, xmax], linewidth=3, label="1/2")
# get half bessel function
ys = besselj.(3/2, xs)
plot!(xs, ys, xlim=[xmin, xmax], linewidth=3, label="3/2")
# get half bessel function
ys = besselj.(5/2, xs)
plot!(xs, ys, xlim=[xmin, xmax], linewidth=3, label="5/2")
# make Newtonian plot
savefig(p, "half_bessel.png")