ねじれアルヴェーン波 (torsional Alfvén waves)

普通の有限振幅の波動は時間とともにその形が崩れ、最終的には衝撃波となることが多いです。しかし、有限振幅のAlfvén波はそのままの形で伝播していくことができます。ここでは有限振幅の円偏光Alfvén波(torsional Alfvén wave)がどのような方程式を満たすかを考察しましょう。

波動方程式の導出

以下、外力や粘性等を無視できるような系を考えます。また磁場が支配的であるとして圧力も無視します。流体の密度も一様を仮定すると、この系の流体要素の運動方程式は

\[\frac{\partial \mathbf{v}}{\partial t} + (\mathbf{v} \cdot \nabla) \mathbf{v} = - \frac{1}{\rho} \nabla \left( \frac{B^2}{8\pi} \right) + \frac{1}{4 \pi \rho} (\mathbf{B} \cdot \nabla) \mathbf{B} \tag{1}\]

最初、磁場は一様磁場\(\mathbf{B}_0 = B_0 \mathbf{e}_z\)で、流体は静止していたとします。ここに円偏光Alfvén波となるような有限の大きさの摂動を加えます。

\[\mathbf{B} = B_0 \mathbf{e}_z + B_\perp (t, z) \mathbf{e}_+ \tag{2}\]

(2)式のように\(\mathbf{B}_0\)に垂直な方向に\(B_\perp\)が加わったとします。ここで\(\mathbf{e}_+\)はヘリシティが正の偏光ベクトルで

\[\mathbf{e}_+ = \frac{1}{\sqrt{2}} (\mathbf{e}_x + i \mathbf{e}_y) \tag{3}\]

です。

注意: プラズマ業界ではヘリシティが正のものを右回りと呼びますが、光学業界ではこれを左回りと呼びます。定義に注意しましょう。

ここで理想磁気流体の状況を考えて、流体は磁場に凍結しているとすると

\[\mathbf{v} (t, z) = \mathbf{v}_\perp = v_\perp(t, z) \mathbf{e}_+ \tag{4}\]

のようになります。(1)式の各項を計算していきましょう。

\[(\mathbf{v} \cdot \nabla) \mathbf{v} = (\mathbf{v}_\perp \cdot \nabla) \mathbf{v}_\perp = v_\perp \frac{1}{\sqrt{2}} \left( \frac{\partial}{\partial x} + i \frac{\partial }{\partial y} \right) v_\perp (t, z) \mathbf{e}_+ = \mathbf{0}\]

\(\mathbf{B} = (B_\perp/\sqrt{2}, i B_\perp / \sqrt{2}, B_0)\)より

\[\nabla B^2 = \nabla B_0^2 = 0\] \[(\mathbf{B} \cdot \nabla) \mathbf{B} = \left\{ \sqrt{B_\perp}{\sqrt{2}} \left( \frac{\partial}{\partial x} + i \frac{\partial}{\partial y}\right) + B_0 \frac{\partial }{\partial z}\right\} \{ B_0 \mathbf{e}_z + B_\perp \mathbf{e}_+\} = B_0 \frac{\partial \mathbf{B}_\perp}{\partial z}\]

これらから(1)式は

\[\frac{\partial \mathbf{v}_\perp}{\partial t} = \frac{B_0}{4\pi \rho} \frac{\partial \mathbf{B}_\perp}{\partial z} \tag{5}\]

誘導方程式

\[\frac{\partial \mathbf{B}}{\partial t} = \nabla \times (\mathbf{v} \times \mathbf{B})\]

から

\[\begin{align} \frac{\partial \mathbf{B}_\perp}{\partial t} &= \nabla \times \{ v_\perp \mathbf{e}_+ \times (B_0 \mathbf{e}_z + B_\perp \mathbf{e}_+)\} = \nabla \times (v_\perp \mathbf{e}_+ \times B_0 \mathbf{e}_z) = \nabla \times \frac{v_\perp B_0}{\sqrt{2}} (- \mathbf{e}_y + i \mathbf{e}_x) \notag \\ &= \frac{B_0}{\sqrt{2}} \left( \begin{array}{c} \frac{\partial}{\partial x} \\ \frac{\partial}{\partial y} \\ \frac{\partial}{\partial z} \end{array}\right) \times \left( \begin{array}{c} i v_\perp \\ -i v_\perp \\ 0 \end{array}\right) = \frac{B_0}{\sqrt{2}} \left( \begin{array}{c} \frac{\partial v_\perp}{\partial z} \\ i \frac{\partial v_\perp}{\partial z} \\ 0 \end{array}\right) = B_0 \frac{\partial v_\perp}{\partial z} \frac{1}{\sqrt{2}} (\mathbf{e}_x + i \mathbf{e}_y) = B_0 \frac{\partial \mathbf{v}_\perp}{\partial z} \tag{6} \end{align}\]

(5), (6)式より

\[\frac{\partial^2 \mathbf{B}_\perp}{\partial t^2} = \frac{\partial}{\partial t} B_0 \frac{\partial \mathbf{v}_\perp}{\partial z} = B_0 \frac{\partial}{\partial z} \frac{\partial \mathbf{v}_\perp}{\partial t} = v_A^2 \frac{\partial^2 \mathbf{B}_\perp}{\partial z^2} \tag{7}\]

これは波動方程式の形をしていることから、有限振幅の円偏波Alfvén波は位相速度\(v_A = B_0 / \sqrt{4\pi \rho}\)で、その形を崩す(途中で衝撃波になったり振幅減衰する)ことなく、伝播できることがわかります。

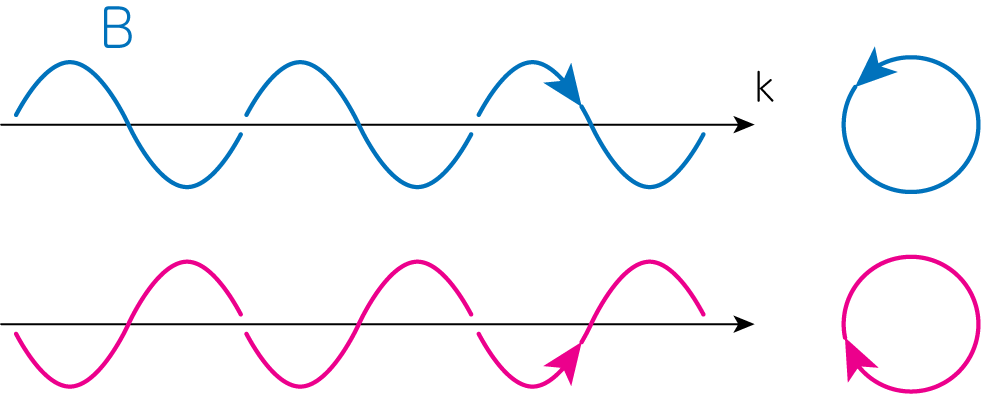
実際の有限振幅アルヴェーン波

有限振幅でも、このAlfvén波は形を崩すことなく伝播することがわかりました。しかし、実際には波長\(\lambda\)の単一波長のAlfvén波は、オーム散逸による磁場の拡散により\(\tau \simeq \lambda^2 / \eta\)の時間スケールで拡散します。他の有限振幅波は波が鋭く突っ立っていき、長さのスケールが\(\lambda\)よりもとても小さくなります。よって他の有限振幅の波が素早く減衰するのに比べて、この波は長い時間、形を維持して伝播していくことができます。
しかし話はそう単純ではありません。実は有限振幅のAlfvén波は非線形相互作用により、Alfvén波の持つエネルギーを音波や流体(ミクロにはプラズマ粒子)の運動エネルギーへと変化させることが可能です。よって結局はこれも素早く減衰する現象が起こります。

参考文献

[1] Priest, “Solar Magnetohydrodynamics”
[2] 観山正見, 野本憲一, 二間瀬敏史, “天体物理学の基礎 II”
[3] 内田岱二郎, Chen, “プラズマ物理入門”