Table of contents
輻射抵抗とポインティング・ロバートソン効果
輻射抵抗 (radiation drag)
次の図のように、真空中を質量\(m\)の粒子が速度\(v\)で\(x\)軸方向に運動しているとします。
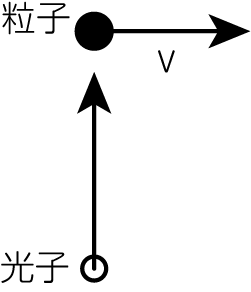
このとき、\(y\)軸方向遠方に輻射源が存在することで、粒子は単位時間あたりに\(\epsilon\)の輻射エネルギーを吸収しながら運動するとしましょう。 この輻射エネルギーを微小時間\(\Delta t\)だけ吸収することで、粒子の質量と速度はそれぞれ\(m', v'\)のように変化したとします。 そしてこののちに、粒子は速やかに光子を等方的に再放射するとします。 この問題設定では、\(v \ll c, \epsilon \Delta t \ll mc^2\)であり、\(y\)方向の粒子の速度変化は無視できるものとします。 するとエネルギー保存則より
\[mc^2 + \epsilon \Delta t = m' c^2 \tag{1}\]です。 そして\(x\)方向の運動量保存則より
\[mv = m' v' \tag{2}\]を得ます。 これらより
\[v' = \frac{m}{m'} v = \frac{m}{m + \frac{\epsilon \Delta t}{c^2}} v \underbrace{\approx}_{\epsilon \Delta t \ll mc^2} v \left( 1 - \frac{\epsilon \Delta t}{mc^2}\right) \tag{3}\]のようになります。 よって得られる速度の変化分は
\[\Delta v = v' - v = -\frac{\epsilon \Delta t}{mc^2} v \tag{4}\]です。 吸収した輻射エネルギーを等方的に再放射することで、粒子の質量は\(m' \rightarrow m\)のように、元に戻ります。 一方で、粒子と同じ速度で運動する共動系において、粒子が等方的に光子を再放射すると、粒子には力は働きません。 ここから、再放射後の粒子の速度は\(v'\)のままであることがわかります。 (4)式の最右辺は負であることから、粒子は減速していることがわかります。 輻射が抵抗力として働いたことから、これを輻射抵抗(radiation drag)と呼びます。
(4)式において、\(\Delta t \rightarrow 0\)のような極限を取ると
のような微分方程式となり、最終的に\(v(t) = v(0) e^{-\frac{\epsilon}{mc^2} t}\)のように解くことができます。
この効果は、下図のように理解することができます。
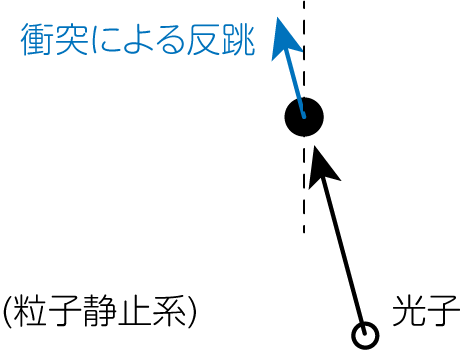
粒子と同じように運動する系に移って考えてみましょう。 粒子から見ると、光子は真横ではなく、斜め前方から飛んでくるように見えます。 この光子との衝突の結果、粒子は斜め後ろに反跳することになります。 これが垂直方向から入射する光子による、輻射抵抗の定性的な理解です。
ポインティング・ロバートソン効果 (Poynting-Robertson effect)
これを実際の宇宙物理系に応用してみましょう。 光度\(L\)、質量\(M\)の点光源天体があり、そこから距離\(r\)の場所にダスト粒子がいるとします。 このダスト粒子は、この天体を中心天体として、重力と遠心力が釣り合う位置で円運動をしていますが、先程の輻射抵抗によりその軌道半径がだんだん小さくなります。 ダスト粒子の質量を\(m\)、方位角方向の速度を\(v_\varphi\)、そしてダスト粒子の吸収散乱断面積を\(\sigma_d\)のように書くことにします。 半径\(r\)の位置での単位時間あたりに流れる輻射エネルギーは\(\frac{L}{4\pi r^2}\)なので、輻射抵抗による力は
\[-\frac{1}{mc^2} \frac{\sigma_d L}{4\pi r^2} v_\varphi \tag{6}\]のように書かれます。 2次元曲座標で運動方程式を書き下すことで得られる方位角方向の運動方程式から、\(\frac{m}{r} \frac{d}{dt} (r v_\varphi) = F_\varphi\)です。 よって
\[\frac{1}{r} \frac{d}{dt} (r v_\varphi) = - \frac{\sigma_d L}{4\pi mc^2} \frac{v_\varphi}{r^2} \tag{7}\]重力と遠心力の釣り合いから、\(v_\varphi \approx \sqrt{\frac{GM}{r}}\)とすると
\[\frac{1}{r} \frac{d}{dt} (\sqrt{GM} r^{1/2}) = \frac{\sqrt{GM}}{r} \frac{1}{2 r^{-1/2}} \dot{r} = \frac{\dot{r}}{2r}\]のように計算されるので、最終的に
\[r \dot{r} = - \frac{\sigma_d L}{2\pi mc^2} \ \Longrightarrow \ r^2 - r_0^2 = \frac{\sigma_d L}{\pi m c^2} t \tag{8}\]のように積分することができます。 途中、\(t=0\)での軌道半径を\(r_0\)のように書きました。 この式において\(r=0\)を代入すると
\[t = \frac{\pi m c^2}{aL} r_0^2 \tag{9}\]のようになります。 すなわち初期に\(r_0\)にいたダスト粒子が、この時間スケールで中心星へと落下していくことがわかります。 ここでダストは球形で、その半径は\(a_d\)であるとします。 またダストの吸収散乱断面積は大雑把に\(\sigma_d \approx \pi a_d^2\)のように計算され、ダスト粒子の密度を\(\rho_d\)とすると\(\frac{4\pi}{3} a_d^3 \rho_d = m\)となります。 これらを用いて(9)式を整理すると
\[t \approx \frac{4 a_d \rho_d c^2 r_0^2}{L} \approx 450 \left( \frac{a_d}{1 \mathrm{\mu m}}\right) \left( \frac{\rho_d}{1 \mathrm{g cm^{-3}}}\right) \left( \frac{L}{L_\odot}\right)^{-1} \left( \frac{r_0}{1 \mathrm{AU}}\right)^2 \ [\mathrm{yr}] \tag{10}\]のようになります。 計算にはダストの典型的な半径を\(1 \mathrm{\mu m}\)、ダストの典型的な密度を\(1 \mathrm{g/cm^3}\)、そして中心星が太陽であるとし、さらにダストの初期位置は地球の公転半径にいるとしました。 太陽系内にはダストが存在していたとしても、それらはこのポインティング・ロバートソン効果で中心星に落ちていくか、あるいは輻射力によってより外側に吹き飛ばされます。 現在の太陽系内に存在するダストは、系内に存在する小天体同士の衝突や、彗星からもたらされたと考えられています。
その他の計算では760年程度になる...近似の仕方による?まぁ同じオーダー程度になったのでヨシ(๑˃̵ᴗ˂̵)و
補遺: もう少し特殊相対論っぽく導出したい場合
粒子が光子を吸収し、その質量を変化させるという効果は、相対論的な効果です。 これまでの導出ももちろんこれを利用してきたわけですが、できればもう少しアドバンスドな(?)導出の仕方もしてみたいと思うかもしれません。 ここでは4元運動量をしっかりと計算することで、輻射抵抗の導出を示します。
\(x\)軸方向に運動しているダスト粒子が、\(y\)軸方向からきた光子を吸収したとします。 初期の粒子の4元運動量を
とし、さらに光子の4元運動量は
\[\hbar k^\mu = \left( \frac{h\nu}{c}, 0, \frac{h\nu}{c}, 0, 0\right) \tag{12}\]です。 吸収前のダスト粒子の速度は、特殊相対論の公式より
\[v_x = \frac{pc^2}{E} \tag{13}\]となります。 これに対して、吸収後のダスト粒子の4元運動量は
\[p'^\mu = \left( \frac{E'}{c}, p'_x, p'_y, 0\right) = \left( \frac{E+h\nu}{c}, p, \frac{h\nu}{c}, 0\right) \tag{13}\]のようになり、\(x\)軸方向の速度は
\[v'_x = \frac{p'_x c^2}{E'} = \frac{pc^2}{E + h\nu} < v_x \tag{14}\]と計算されます。 ここから、\(x\)軸方向の運動量は変化しないにもかかわらず、エネルギーが増えたために、\(x\)軸方向の速度が減少することがわかります。
参考文献
[1] 梅村雅之, 福江純, 野村英子, “輻射輸送と輻射流体力学”
[2] 高原文郎, “特殊相対論”
[3] 太田浩一, “電磁気学の基礎 II”