Table of contents
ぺチェックの磁気リコネクション (Petscheck reconnection)
磁力線のつなぎかわりは中心の小さな磁気拡散領域で行い、エネルギーの変換は拡散領域から外側に伸びるスローショック部分で実現しようというモデルです。これによるリコネクション時間スケールは中心の拡散領域のサイズで決定されるので、それを十分小さくすることで短い時間スケールを実現することが可能となりました。

リコネクション率
簡単のため、リコネクション領域以外では2次元定常非圧縮を仮定します。非圧縮より
\[\nabla\cdot {\bf v} = 0\]マスクウェル方程式より
\[\nabla\cdot {\bf B} = 0\]衝撃波面の法線方向を\(n\)、接線方向を\(t\)とすると
\[v_{In}=v_{IIn} \tag{1}\] \[B_{In}=B_{I\hspace{-.1em}I n} \tag{2}\]ここでI, IIはそれぞれ衝撃波面前と衝撃波面後の領域の物理量を意味する添字です。
接線方向の運動量保存則より
\[\rho v_{It} v_{In} - \frac{1}{4\pi} B_{It} B_{In} = \rho v_{I\hspace{-.1em}I t} v_{I\hspace{-.1em}I n} - \frac{1}{4\pi} B_{I\hspace{-.1em}I t} B_{I\hspace{-.1em}I n} \tag{3}\] \[(1), (2), (3) \ \Longrightarrow \ \rho v_{I n} (v_{It}-v_{I\hspace{-.1em}I t}) = \frac{1}{4\pi} B_{I n} (B_{I t} - B_{I\hspace{-.1em}I t}) \tag{4}\]誘導方程式より
\[\frac{\partial {\bf B}}{\partial t} = \nabla \times({\bf v} \times {\bf B}) = {\bf 0}\]この両辺を衝撃波面に垂直な面で積分すると、ストークスの定理より
\[\begin{align} & \iint \nabla \times ({\bf v} \times {\bf B}) \cdot d{\bf S} = \oint ({\bf v} \times {\bf B}) \cdot d{\bf s} = 0 \notag \\ & \Longrightarrow \ (v_{I t} B_{I n} - B_{I t} v_{I n}) \ell - (v_{I\hspace{-.1em}I t} B_{I\hspace{-.1em}I n} - B_{I\hspace{-.1em}I t} v_{I\hspace{-.1em}I n}) \ell = 0 \notag \\ & \Longrightarrow \ v_{I n} (B_{I t} - B_{I\hspace{-.1em}I t}) = B_{I n} (v_{I t} - v_{I\hspace{-.1em}I t}) \notag \end{align}\]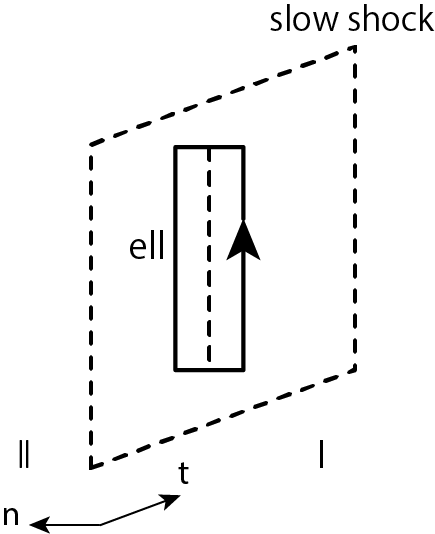
この結果と(4)式より
\[v_{I n}^2 = \frac{B_{I n}^2}{4\pi \rho} \tag{5}\]衝撃波による磁場および流線の傾きは十分小さいと考えると
\[B_{I\hspace{-.1em}I t} \simeq v_{I t} \sim 0\]と近似できるので
\[v_{I\hspace{-.1em}I} \simeq v_{I\hspace{-.1em}I t} = \frac{v_{I n}}{B_{I n}} B_{I t} = \frac{B_{I t}}{\sqrt{4\pi \rho}} \simeq \frac{B_{I}}{\sqrt{4\pi \rho}} = v_A \tag{6}\]となります。
マクスウェル方程式より、領域Iで定常なので磁場は\(\nabla \times {\bf B} = {\bf 0}\)と書けます。よって磁場は
\[{\bf B} = -\nabla \phi\]となるようなポテンシャルが存在します。\(\nabla \times {\bf B} = {\bf 0}\)を満たすような磁場の形として
\[B_x = A_1 - C_1 \ln \frac{L}{\sqrt{x^2+y^2}}\] \[B_y = C_1 \left( \frac{\pi}{2} - \tan^{-1} \frac{y}{x} \right) \tag{7}\]ここで\(A_1, C_1\)は積分定数です。この磁場とオームの法則\({\bf j} = \sigma ({\bf E} + \frac{1}{c} {\bf v} \times {\bf B})\)より
\[{\bf E} = \frac{1}{\sigma} {\bf j} - \frac{1}{c} {\bf v} \times{\bf B} = \frac{c}{4\pi \sigma} \nabla \times {\bf B} - \frac{1}{c} {\bf v} \times {\bf B} \simeq {\bf 0}\]領域I, IIの境界に存在する中間領域の速度・磁場に*をつけて考えましょう。上式で微分を微少量\(\delta\)で考えると
\[v_I^* B_I^* \simeq \frac{c^2}{4\pi \sigma} \frac{B_I^*}{\delta} = \frac{L v_A }{\rm{R}_m} \frac{B_I^*}{\delta}\]ここで(5)より、領域Iでは\(v_I \simeq v_A\)から、中間領域の速度も同じ程度のオーダーと考えると
\[v_I^* \simeq v_A\]これらより
\[{\rm R}_m \simeq \frac{L}{ \delta} \tag{8}\]これが領域I, IIの接続条件になります。
リコネクション領域へのエネルギー流入量(リコネクション率)は
\[\frac{d E_{\rm mag}}{dt} = \frac{B_I^2}{4\pi } L^2 v_I\]エネルギーの流出量は
\[E_{\rm mag} = \frac{B_{I\hspace{-.1em}I}^2}{8\pi} L^3\]接続条件(8)と磁場をポテンシャル表現、そして中間領域では磁場がおよそ\(\alpha\)分の一の大きさになるという条件\(B_{Ix}^* \simeq B_{Ix}/\alpha\)を付加すると
\[B_{Ix}^* \simeq \frac{B_{Ix}}{\alpha} = B_{Ix} - C_1 \ln {\rm R}_m \ \Longrightarrow \ C_1 = \frac{\alpha-1}{\alpha}\frac{B_{Ix}}{\ln {\rm R}_m} \tag{9}\]磁気流体の斜め衝撃波では\(v_{Iy} B_{Ix} = v_{Iy}^* B_{Ix}^* = v_{I\hspace{-.1em}I x} B_{I\hspace{-.1em}I y}\)が成り立つので(6), (7), (9)式より
\[\frac{v_{Iy}}{v_A} = \frac{\alpha -1}{\alpha}\frac{\pi}{8} \frac{1}{\ln {\rm R}_m}\]ここで簡単のために\(\alpha = 2\)としてみましょう。すると
\[\frac{v_{Iy}}{v_A} \simeq \frac{\pi}{8} \frac{1}{\ln {\rm R}_m}\]となります。
リコネクションの時間スケール
\[t_{\rm P} \simeq \frac{B_{Ix}^2/(8\pi) L^3}{B_{Ix}^2/(4\pi) v_{Iy} L^2 } \simeq \frac{8}{\pi} \ln {\rm R}_m t_A \simeq (10-100) t_A\]ここで\(t_A\)はアルヴェーン横断時間(Alfven crossing timescale, アルヴェーン速度で系を横断するのにかかる時間)です。このリコネクションモデルは太陽フレアの観測によく一致します。
ぺチェック磁気リコネクションの問題点
しかしこの解をそのまま太陽フレアに適用しようとすると、中心となるリコネクション領域の厚み\(\delta\)が1cm以下になります。これがどのくらい小さいかを実感するために、イオンのラーモア半径(Larmor radius)を考えましょう。
\[r_{\rm L, ion} = \frac{m_p v c}{eB} \simeq 10 \left( \frac{T}{10^6{\rm K}}\right)^{1/2} \left( \frac{B}{100 {\rm G}}\right)^{-1} \ {\rm cm}\]途中\(m_p v^2 = 2 k_B T, m_p c^2 \simeq 938{\rm MeV}\)などを用いて計算を行いました。リコネクション領域の厚みに比べてイオンのラーモア半径の方が大きいため、この系での理想磁気流体近似は適切ではありません。ここではプラズマ粒子の運動論的扱いが必要になってきます。ぺチェックのリコネクションモデルは非相対論/相対論的抵抗性磁気流体の問題として、シミュレーションで活発に研究が行われています。
参考文献
[1] 桜井隆, 小島正宣, 小杉健郎, 柴田一成, “シリーズ現代の天文学 太陽”
[2] Priest, “Solar Magnetohydrodynamics”