Table of contents
デバイ・ヒュッケルの理論 (Debye-Hückel theory)
デバイ長 (Debye length)
電気的に中性で無限に広がった電子・陽子からなる完全電離水素ガスの弱結合プラズマ中に、点電荷\(q_0\)を加えたときの静電場の様子を調べましょう。 ただし陽子の質量は電子よりも非常に大きく、点電荷が加わったとしても影響を受けないとして、ここでは電子のみを考えます。 統計力学によると、温度\(T\)で熱平衡にある粒子系では、粒子のエネルギーが\(E \sim E + dE\)の範囲にある確率は
\[P(E) dE \propto e^{-E/k_B T} dE \tag{3}\]で与えられます。 特に自由な非相対論的運動をしている粒子系では、速度が\(\mathbf{v} = (v_x, v_y, v_z) \sim \mathbf{v} + d\mathbf{v} = (v_x + dv_x, v_y + dv_y, v_z + dv_z)\)の範囲にある確率は
\[P(\mathbf{v}) dv_x dv_y dv_z = \left( \frac{m}{2\pi k_B T} \right)^{3/2} e^{-mv^2 / 2 k_B T} dv_x dv_y dv_z \tag{4}\]のように与えられます。 これをマクスウェル・ボルツマン分布(Maxwell-Boltzmann distribution: Maxwellian)と呼びます。 ここで\(m\)は粒子系を構成する粒子の質量、そして\(v^2 = v_x^2 + v_y^2 + v_z^2\)です。 電子が存在する領域の体積を\(V\)、そして電子がこの体積内に一様に分布しているとしましょう。 電子のクーロンポテンシャルエネルギー\(-e \phi(\mathbf{r})\)が存在するとき、電子のエネルギーは
\[E = \frac{1}{2} m_e v^2 - e\phi(\mathbf{r}) \tag{5}\]で与えられます。 ある位置\(\mathbf{r} \sim \mathbf{r} + d\mathbf{r}\)で速度が\(\mathbf{v} \sim \mathbf{v} + d\mathbf{v}\)の範囲の電子が見つかる確率は
\[P(\mathbf{r}) P(\mathbf{v}) d^3 \mathbf{r} d^3 \mathbf{v} = C_1 e^{\frac{-m_e v^2 / 2 + e \phi(\mathbf{r})}{k_B T}} d^3 \mathbf{r} d^3 \mathbf{v} \tag{6}\]のようになります。 ここで\(C_1\)は規格化定数です。 この両辺を、まず全速度空間で体積積分しましょう。
\[\begin{align} \underbrace{\iiint_{-\infty}^\infty P(\mathbf{v}) d^3 \mathbf{v}}_{=1} P(\mathbf{r}) d^3 \mathbf{r} &= C_1 e^{\frac{e\phi (\mathbf{r})}{k_B T}} d^3 \mathbf{r} \int_{-\infty}^\infty dv_x \int_{-\infty}^\infty dv_y \int_{-\infty}^\infty dv_z e^{-\frac{m_e (v_x^2 + v_y^2 + v_z^2)}{k_B T}} \notag \\ &= C_1 e^{\frac{e\phi (\mathbf{r})}{k_B T}} d^3 \mathbf{r} \left( \int_{-\infty}^\infty dv_x e^{-\frac{m_e v_x^2}{k_B T}}\right)^3 \tag{7} \end{align}\]ガウス積分の公式より
\[\int_{-\infty}^\infty dv_x e^{-\frac{m_e v_x^2}{k_B T}} = \sqrt{\frac{2k_B T \pi}{m_e}} \tag{8}\]と計算できるので
\[P(\mathbf{r}) d^3 \mathbf{r} = C_1 \left( \frac{2\pi k_B T}{m_e}\right)^{3/2} e^{\frac{e\phi (\mathbf{r})}{k_B T}} d^3 \mathbf{r} \tag{9}\]となります。 この両辺をさらに体積\(V\)で積分しましょう。
\[\underbrace{\iiint_V P(\mathbf{r}) d^3 \mathbf{r}}_{=1} = C_1 \left( \frac{2\pi k_B T}{m_e}\right)^{3/2} \underbrace{\iiint_V e^{\frac{e\phi (\mathbf{r})}{k_B T}} d^3 \mathbf{r}}_{\equiv C_2} \ \Longrightarrow \ C_1 = \left( \frac{m_e}{2\pi k_B T}\right)^{3/2} \frac{1}{C_2} \tag{10}\]途中、体積積分部分は計算ができそうにないため、適当な定数\(C_2\)としました。 このようにして規格化定数\(C_1\)が求まったため、(9)式より
\[P(\mathbf{r}) d^3 \mathbf{r} = \frac{1}{C_2} e^{\frac{e\phi(\mathbf{r})}{k_B T}} d^3 \mathbf{r} \tag{11}\]ここで\(V \rightarrow \infty\)の極限を考え、無限遠方では\(\phi (\mathbf{r}) \rightarrow 0\)とします。 そして無限遠での電子数密度を\(n_{e0}\)、任意の位置\(\mathbf{r}\)での電子の数密度を\(n_e (\mathbf{r})\)のようにしましょう。 ある微小領域\(\mathbf{r} \sim \mathbf{r} + d\mathbf{r}\)に電子が存在する確率は
\[P(\mathbf{r}) d^3 \mathbf{r} = \frac{d^3 \mathbf{r}内にいる電子数}{全電子数} = \frac{n_e (\mathbf{r}) d^3 \mathbf{r}}{N} \tag{12}\]と書くことができます。 この式と(11)式より
\[\frac{n_e (\mathbf{r}) d^3 \mathbf{r}}{N} = \frac{1}{C_2} e^{\frac{e\phi(\mathbf{r})}{k_B T}} d^3 \mathbf{r} \ \Longrightarrow \ n_e (\mathbf{r}) = \frac{N}{C_2} e^{\frac{e\phi(\mathbf{r})}{k_B T}} \tag{13}\]\(\vert \mathbf{r} \vert \rightarrow \infty\)では、点電荷によるポテンシャルの影響はなくなり\(n_e \rightarrow n_{e0}\)になるという境界条件から、電子数密度が
\[n_e (\mathbf{r}) = n_{e0} e^{\frac{e\phi(\mathbf{r})}{k_B T}} \tag{14}\]で与えられることが分かります。 この結果を見ると、ポテンシャルエネルギー\(-e\phi\)がより低いところ(\(\phi\)の値が大きなところ)に電子が集まることが分かります。
元々の問題に立ち返ると、今は電子と陽子からなる完全電離水素ガスを考えているのでした。 よって無限遠方では電子と陽子の密度が等しくなっているはずです。 そして最初に述べたように、陽子は電子に比べて非常に重たく、電荷が加わったとしても至るところで一様に分布していると考えることができるため、陽子の数密度分布は\(n_p = n_{e0}\)と与えることができます。
ここで弱結合プラズマという条件を導入しましょう。 するとこれは
の条件が成り立つことを意味します。 ここから、(14)式の電子数密度分布をテイラー展開すると
\[n_e(\mathbf{r}) \simeq n_{p} \left( 1 + \frac{e\phi(\mathbf{r})}{k_B T}\right) \tag{16}\]と求まります。 中心に置いた電荷\(q_0\)が作る静電ポテンシャルは、電磁ポテンシャルを求める方程式にローレンツゲージを課したものより
\[\Delta \phi (\mathbf{r}) = -4\pi \rho \tag{17}\]から求めることができます。 ここで系は一定の状態に落ち着いていると考えて\(\frac{\partial}{\partial t} = 0\)としました。 右辺の\(\rho\)は電荷密度です。 以上から、一様プラズマの原点に点電荷\(q_0\)を置いたときのポアソン方程式は
\[\begin{align} &\Delta \phi (\mathbf{r}) = - 4\pi q_0 \delta^3 (\mathbf{r}) - 4\pi (en_p - en_e(\mathbf{r})) \simeq - 4\pi q_0 \delta^3 (\mathbf{r}) + 4\pi e n_p \frac{e\phi (\mathbf{r})}{k_B T} \notag \\ &\Longrightarrow \ \left( \Delta - \frac{1}{\lambda_D^2} \right) \phi = - 4\pi q_0 \delta^3 (\mathbf{r}) \tag{18} \end{align}\]のようになります。 ここで\(\lambda_D\)はデバイ長(Debye length)と呼ばれる長さの次元を持った量です。 具体的に評価すると
\[\begin{align} \lambda_D &\equiv \sqrt{\frac{k_B T}{4\pi e^2 n_e}} \simeq \sqrt{\frac{\left( \frac{T}{10^4 \mathrm{K}}\right) \mathrm{eV}}{4\pi \frac{e^2}{\hbar c} \hbar c n_e}} \simeq \sqrt{\frac{T}{10^4 \mathrm{K}} \mathrm{eV} \frac{1}{\frac{4\pi n_e}{137} 197 \mathrm{MeV} \cdot \mathrm{fm}}} \notag \\ &\simeq \sqrt{\frac{T}{10^4 \mathrm{K}} \frac{1}{\frac{120}{7} \times 10^{-7} n_e}} \simeq 7 \times 10^2 \left( \frac{T}{10^4 \mathrm{K}}\right)^{1/2} \left( \frac{n_e}{1 \mathrm{cm}^{-3}}\right)^{-1/2} \quad [\mathrm{cm}] \tag{19} \end{align}\]のようになります。 さらに、(18)式の解は以下のように求まります(導出は湯川型ポテンシャルの導出ページを参照)。
\[\phi (r) = \frac{q_0}{r} e^{-r/\lambda_D} \tag{20}\]この結果は、プラズマの存在により点電荷からデバイ長以上離れると、静電ポテンシャルが急激に減少することを表しています。 これは中心の電荷によるクーロン力の到達距離が\(r < \lambda_D\)に限られる、と言い換えることもできます。
デバイ遮蔽 (Debye shielding)
(20)式でポテンシャルが表される現象を詳細に見てみましょう。 そのために、まずは空間でのプラズマの全電荷を調べてみます。
\[\begin{align} \int_{+0}^\infty 4\pi r^2 e(n_p - n_e(\mathbf{r})) &= - \int_{+0}^\infty 4\pi r^2 e^2 \frac{\phi (\mathbf{r})}{k_B T} dr = - \int_{+0}^\infty r q_0 e^{-r/\lambda_D} \underbrace{\frac{4\pi n_{e0} e^2}{k_B T}}_{=1/ \lambda_D^2} \notag \\ &= - q_0 \int_{+0}^\infty \frac{r}{\lambda_D} e^{-r/\lambda_D} \frac{dr}{\lambda_D} = - q_0 \tag{21} \end{align}\]これは中心に置いた点電荷の電荷を打ち消す量になっていることが分かります。 もともと電気的中性が保たれていたプラズマから全電荷が\(-q_0\)が発生したようにも見えるかもしれませんが、これは中心の電荷\(q_0\)をイオンの一部を寄せ集めて作ったものと考えれば良いでしょう。 電子分布の一様分布からのズレができたことで、中心にできた電荷の偏りと打ち消しあい、遠方にいる観測者にとっては電気的中性が保たれているように見えます。 この電荷の遮蔽現象をデバイ遮蔽(Debye shielding)と呼びます。 デバイ長は電子の平均間隔より十分大きく、中心の電荷からデバイ長を半径とする球内に入っている電子の数は
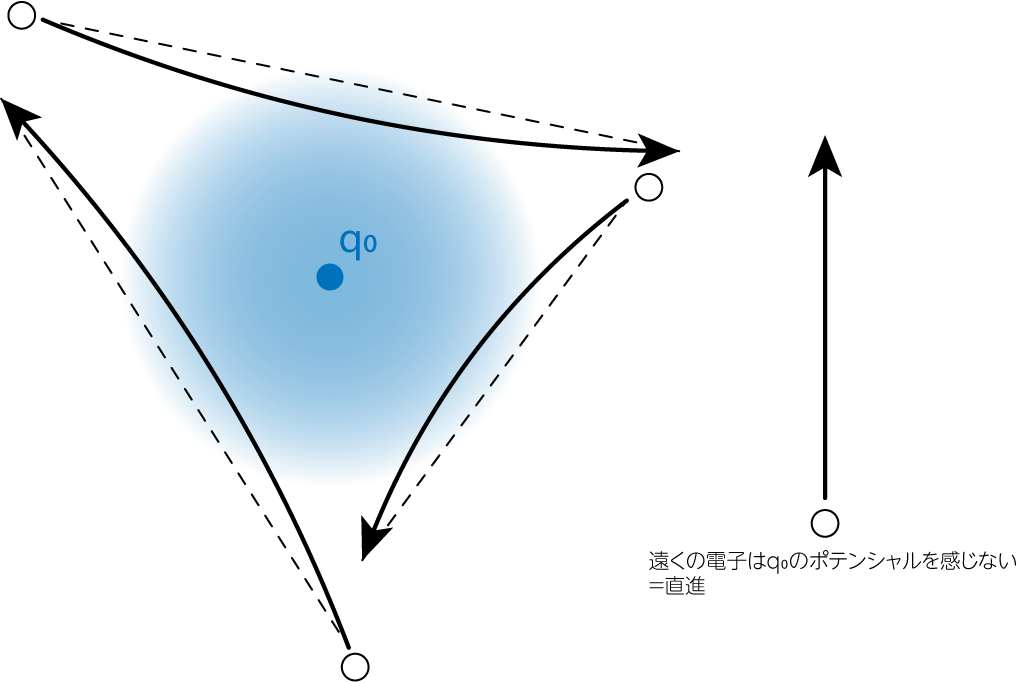
\[\Lambda_c \equiv \frac{4\pi}{3} \lambda_D^3 n_e \simeq 1 \times 10^9 \left( \frac{T}{10^4 \mathrm{K}}\right)^{3/2} \left( \frac{n_e}{1 \mathrm{cm}^{-3}}\right)^{-3/2} \tag{22}\]のようになり、非常に多いことが分かります。 このことから電荷の遮蔽現象は、非常に多数の電子によって行われていると理解できます。 一方、デバイ長は電子の平均自由行程と比べると十分短く、デバイ遮蔽を引き起こす電子と電子どうしあるいはイオンとの衝突は無視できます。 このことから、デバイ遮蔽は無衝突プラズマの特徴的現象であると分かります。 例えば\(q_0>0\)の場合を考えましょう。 このときの静電ポテンシャルは\(\phi > 0\)より、中心部に負の電荷を持つ電子が偏って分布していることになります。 これは以下のようにして起こります。 中心に電荷がないときは直進していたはずの電子の軌道は、電荷の存在により中心に惹きつけられて少し曲がります。 軌道の変化が少量であることは、弱結合プラズマであることから保証されます。 一つの電子の軌道の変化による遮蔽効果は非常に小さいですが、多数の電子に同様の軌道変化が起きることで、デバイ波長程度離れると中心においた電荷がほぼ遮蔽されるのです。 無衝突なのに個々の電子が協調的に振る舞うことで、集団で一つの現象を引き起こすプラズマ現象の典型的な例です。 現実世界でも同様の例を見つけることができます。 アイドルが人の多い場所に突然現れたとしましょう。 すると周囲にいる人々はアイドルに握手やサインを求めます。 またある人はアイドルを一目見ようと距離を縮めたり、その姿をスマホカメラに収めようとします。 アイドルを一目見ることができて目的を達成した人はその場から離れていきます。 このように、人だかりを構成する人は入れ替わり立ち替わりが変わっていきいますが、中心にいるアイドルの周囲には常に人だかりが維持されます。 プラズマも人間も、集団的振る舞いという意味では同じ性質を持っているのかも知れません。
最後に、弱結合プラズマの条件を、デバイ長を用いて書き換えてみましょう。 粒子間の静電ポテンシャルと熱運動エネルギーの比は
\[\begin{align} \Gamma &= \frac{e^2 n_{e0}^{1/3}}{\frac{3}{2} k_B T} = \frac{2}{3} \underbrace{\frac{4\pi e^2 n_{e0}}{k_B T}}_{\lambda_D^{-2}} \frac{1}{4\pi n_{e0}^{2/3}} = \frac{1}{6\pi} \frac{1}{\lambda_D^2 n_{e0}^{2/3}} = \frac{1}{6\pi} \underbrace{\left( \frac{4\pi}{3} \lambda_D^3 n_{e0} \right)^{-2/3}}_{=\Lambda_c^{-2/3}} \left( \frac{4\pi}{3}\right)^{2/3} \notag \\ &\simeq \frac{1}{\Lambda_c^{2/3}} \tag{23} \end{align}\]のようになります。 この式からも、プラズマが弱結合であるということとデバイ遮蔽に関わる電子数が非常に多数であることが関係していると分かります。
電子がイオンにより散乱される平均自由行程\(\lambda_e\)についても考察しましょう。 ラザフォード散乱の散乱断面積より
途中、\(\frac{1}{2} m_e v_0^2 \simeq \frac{3}{2} k_B T\)を用いました。 平均自由行程の定義より
\[\begin{align} &\lambda_e = \frac{1}{\sigma_R n_p} = \frac{9}{\pi n_e} \left( \frac{k_B T}{e^2} \right)^2 \underbrace{=}_{(19)} 9 \times 16 \pi n_e \lambda_D^4 \notag \\ &\Longrightarrow \ \frac{\lambda_D}{\lambda_e} = \frac{1}{9 \times 4 \times 3 \frac{4\pi}{3} n_e \lambda_D^3} \underbrace{\simeq}_{(22)} \frac{1}{\Lambda_c} \tag{25} \end{align}\]と計算されます。(23), (25)式より
\[\Gamma \simeq \frac{1}{\Lambda_c^{2/3}} \simeq \left( \frac{\lambda_D}{\lambda_e} \right)^{2/3} \tag{26}\]と求まります。 ここから、デバイ長スケールではプラズマは無衝突プラズマとして扱えることが、改めて確認できました。
コラム的な?: 湯川型ポテンシャル
デバイ・ヒュッケルの理論のデバイ長を、\(\pi\)中間子のコンプトン波長\(\lambda_\pi = \frac{\hbar}{m_\pi c} \sim 1 \mathrm{fm}\)、\(q_0\)を強い力のチャージ\(q_\mathrm{strong}\)に置き換えると、強い力のポテンシャルが得られます。 これは湯川秀樹により初めて提案された理論で
\[\phi = \frac{q_\mathrm{strong}}{r} e^{-r / \lambda_\pi} \tag{27}\]の形のポテンシャルが有名になったため、このタイプのポテンシャルを湯川ポテンシャルあるいは湯川型と呼ぶことがあります。