Table of contents

Random Matrix
Appendix A: 行列のトレースの公式 (3.3)式の証明
Appendix B: 途中の予想が正しいことの証明
参考文献及びリンク

Random Matrix

ランダム行列の定義は、各成分が何かの確率分布にしたがって生成されたような行列です。この講義ではすでに\(J_{ij}\)という形で、それを使ってきました。よって、スピングラスの解析手法をこのトピックに応用することができます。

Distribution of eigenvalues (固有値の分布)

行列\(A\)の固有値分布は以下のように表現されます。

\[\rho (\lambda) = \frac{1}{N} \sum_{i=1}^N \left[ \delta (\lambda - \lambda_i) \right]_A \tag{3.1}\]

ここで\(\lambda_i\)はランダム行列\(A\)の\(i\)番目の固有値です。

デルタ関数について考える

これまではデルタ関数をフーリエ積分表示することで式変形を進めてきましたが、ここでは少し違う見方をします。

\[\delta (\lambda - \lambda_i) = \lim_{\epsilon \rightarrow 0} \frac{1}{\pi} {\rm Im} \left( \frac{1}{\lambda - \lambda_i - i \epsilon} \right) \tag{3.2}\]

ここでは(3.2)式のように\(\lambda\)という形にすることが重要です。この形は固有値の対角化、特に逆行列を対角化するときに出てくる形です。よって(3.2)式を逆行列と対応させることで、何か関係式を導くことができそうです。(3.1), (3.2)式より

\[\rho (\lambda) = \frac{1}{\pi N} \sum_{i=1}^N \left[ {\rm Im} \left( \frac{1}{\lambda - \lambda_i - i\epsilon} \right) \right]_A = \frac{1}{\pi} \frac{\partial}{\partial \lambda} {\rm Im} \left[ \left( \frac{1}{N} \sum_{i=1}^N \log (\lambda - \lambda_i) \right]_A \right)\]

ここで

\[{\rm Tr} [\log (\lambda I - A)] = \log [{\rm det} (\lambda I - A)] \tag{3.3}\]

の公式を用いると

\[\rho (\lambda) = \frac{1}{\pi} \frac{\partial }{\partial \lambda} {\rm Im} \left( \frac{1}{N} \left[ \log [{\rm det} (\lambda I -A)] \right]_A \right) \tag{3.4}\]

物理でdeterminantを良く目にするものとして、多変数のガウス積分が挙げられます。よって人工的なシステムの分配関数として

\[Z (\lambda) = \int d{\bf{u}} \ \exp \left( -\frac{1}{2} {\bf{u}}^T (\lambda I - A) {\bf{u}} \right) = \sqrt{\frac{(2\pi)^N}{\mathrm{det} (\lambda I- A)}} \tag{3.5}\]

ここで\({\bf{u}}\)は人工的な自由度を表すスピン変数です。(3.4), (3.5)式より

\[\rho (\lambda) = - \frac{2}{\pi} \frac{\partial }{\partial \lambda} {\rm Im} ([\log Z(\lambda)]_A) \tag{3.6}\]

よって、この分布を計算したければ\(\log Z (\lambda)\)を計算せよ、という問題に帰着させることができました。これは前回勉強したレプリカ法で計算することができます。

Wigner’s semi-circle low (ウィグナーの半円則)の再現

ここでランダム行列\(A\)の分布が以下のように、ガウス分布で与えられるとしましょう。

\[P (A) = \left( \sqrt{\frac{N}{2\pi}} \right)^{N(N+1)} \exp \left( -\frac{N}{2} \sum_{i < j} A_{ij}^2 - \frac{N}{2} \sum_i A_{ii}^2\right) \tag{3.7}\]

レプリカ法より、\([\log Z(\lambda)]_A\)の代わりに\([Z^n (\lambda)]_A\)を計算します。

\[[Z^n (\lambda)]_A = \prod_{a} \int d{\bf{u}}_a \underbrace{\exp \left( - \frac{\lambda}{2} \sum_{a=1}^n {\bf{u}}_a^T {\bf{u}} \right)}_{(\odot)} \underbrace{\left[ \exp \left( \frac{1}{2} \sum_{a=1}^n {\bf{u}}_a^T A {\bf{u}} \right) \right]_A}_{=(\ast)} \tag{3.8}\]

対角成分の計算

ますは(3.8)式の\((\ast)\)の対角成分を計算しましょう。

\[\begin{align} \left[ \exp \left( \frac{1}{2} A_{ii} \sum_{a=1}^n u_{i, a}^2 \right) \right]_A &\underbrace{=}_{(3.7)} \int dA_{ii} \ \exp \left( - \frac{N}{2} A_{ii} + \frac{1}{2} A_{ii} \sum_a u_{i, a}^2 \right) \notag \\ &= \int dA_{ii} \ \exp \left( - \frac{N}{2} (A_{ii}- \frac{1}{2N} \sum_a u_{i, a}^2)^2 + \frac{1}{8N} (\sum_a u_{i, a})^2 \right) \notag \\ &\propto \int dA_{ii} \ \exp \left( \frac{1}{8N} (\sum_a u_{i, a})^2 \right) \tag{3.9} \end{align}\]

非対角成分の計算

続いて(3.8)式の\((\ast)\)の非対角成分を計算しましょう。

\[\begin{align} \left[ \exp \left( \frac{1}{2} \sum_a \sum_{i \neq j} u_{i, a} A_{ij} u_{j, a} \right) \right]_A &= \left[ \exp \left( \sum_a \sum_{i < j} u_{i, a} A_{ij} u_{j, a} \right) \right]_A \notag \\ &\underbrace{=}_{(3.7)} \int dA_{ij} \ \exp \left( -\frac{N}{2} A_{ij}^2 + A_{ij} \sum_a u_{i, a} u_{j, a} \right) \notag \\ &= \int dA_{ij} \ \exp \left( -\frac{N}{2} (A_{ij} - \frac{1}{N} \sum_a u_{i, a} u_{j, a})^2 + \frac{1}{2N} \left( \sum_a u_{i, a} u_{j, a} \right)^2 \right) \notag \\ &\propto \int dA_{ij} \ \exp \left( \frac{1}{2N} \left( \sum_a u_{i, a} u_{j, a} \right)^2 \right) \tag{3.10} \end{align}\]

秩序変数の導入

(3.8)の\((\odot)\)部分の\(e\)の肩から

\[- \frac{\lambda N}{2} \sum_a \left( \frac{1}{N} \sum_{i=1}^N u_{i, a} u_{i, a}\right) = - \frac{\lambda N}{2} \sum_a q^{aa} \tag{3.11}\]

そして(3.9)式の\(e\)の肩は

\[\frac{1}{8N} \sum_{i=1}^N \sum_{a, b} \underbrace{u_{i, a}^2}_{=1} \underbrace{u_{i, b}^2}_{=1} = \mathcal{O} (1) \tag{3.12}\]

途中の\(\sum_{i=1}^N\)は全ての対角成分での平均をとることからきています。

(3.10)式の\(e\)の肩は

\[\begin{align} \frac{1}{2N} \sum_{i < j} \sum_{a, b} u_{i, a} u_{j, a} u_{i, b} u_{j, b} &= \frac{1}{2N} \sum_{i < j} \sum_{a, b} u_{i, a} u_{i, b} u_{j, a} u_{j, b} = \frac{1}{4N} \sum_{a, b} \left\{ \left( \sum_i u_{i, a} u_{i, b} \right)^2 - \sum_i (u_{i, a} u_{i, b})^2\right\} \notag \\ &\simeq \frac{N}{4} \sum_{a, b} \left( \frac{1}{N} \sum_{i=1}^N u_{i, a} u_{i, b} \right)^2 = \frac{N}{4} \sum_{a, b} (q^{ab})^2 \tag{3.13} \end{align}\]

途中の近似は第1項が\(\mathcal{O} (N^2)\)に対して、第2項が\(\mathcal{O}(N)\)なので、これを無視したことからくるものです。
以上より、\(e\)の肩の合計は

\[N \left( - \frac{\lambda}{2} \sum_a q^{aa} + \frac{1}{4} \sum_{a, b} (q^{ab})^2 \right) \equiv N g(Q) \tag{3.14}\]

となります。ここで\(Q = (q^{ab})\)はスピン秩序パラメータを成分に持つような行列です。よって(3.8)式は、デルタ関数の公式によるテクニックを用いて

\[[Z^n]_A = N \int dQ \ \prod_{a} \int {\bf{u}}_a \ \exp (Ng(Q)) \prod_{a, b} \delta \left( N q^{ab} - \sum_{i=1}^N u_{i, a} u_{i, b} \right) \tag{3.15}\]

となります。\(\prod_a \int d{\bf{u}}_a \prod_{a, b} \delta (N q^{ab})\)は、\(q^{ab}\)で条件付けされた状態数を数えることに対応するので、これはエントロピーです。

(3.15)式の指数部分をエネルギーと見ることもできます。ランダム行列の熱力学などの発展ができそう？

\[\therefore \ (3.15) = \int dQ \ \exp (Ng(Q) + NS(Q)) \tag{3.16}\]

\(N = e^{\log N}\)は他の部分に比べて寄与が小さいとして、無視しました。

エントロピーの計算

では先ほど指摘したエントロピー部分を計算しましょう。デルタ関数をフーリエ積分表示して

\[\prod_{a, b} \delta \left( N q^{ab} - \mathbf{u}_a^T \bf{u}_b \right) = \prod_{a, b} \int d\tilde{Q} \ \exp \left( \frac{1}{2} \tilde{q}^{ab} (N q^{ab} - \mathbf{u}_a^T \mathbf{u}_b )\right) \tag{3.16}\]

この計算を進めるために、レプリカ対称性を導入しましょう。

\[Q = \left( \begin{array}{cccc} Q & q & \cdots & q \\ q & Q & \ddots & \vdots \\ \vdots & \ddots & \ddots & q\\ q & \cdots & q& Q \end{array} \right), \ \tilde{Q} = \left( \begin{array}{cccc} \tilde{Q} & \tilde{q} & \cdots & \tilde{q} \\ \tilde{q} & \tilde{Q} & \ddots & \vdots \\ \vdots & \ddots & \ddots & \tilde{q} \\ \tilde{q} & \cdots & \tilde{q} & \tilde{Q} \end{array} \right) \tag{3.17}\]

すると

\[(3.16)の積分部分 = \prod_a \int d\tilde{Q} \ \exp \left( \frac{1}{2} \tilde{Q} (NQ - {\bf{u}}_a^T {\bf{u}}_a )\right) \prod_{a \neq b} \int d\tilde{q} \ \exp \left( - \frac{1}{2} \tilde{q} (Nq - {\bf{u}}_a^T {\bf{u}}_a )\right) \tag{3.18}\]

途中、簡略化のために\(\tilde{q} \rightarrow - \tilde{q}\)のように変数変換しました。ここに出てくる

\[\prod_{a \neq b} \exp \left( \frac{1}{2} \tilde{q} {\bf{u}}_a^T {\bf{u}}_b \right) = \exp \left( \frac{1}{2} \tilde{q} \sum_{a \neq b} {\bf{u}}_a^T {\bf{u}}_b \right) = \exp \left[ \frac{1}{2} \tilde{q} \left\{ \left( \sum_a {\bf{u}}_a \right)^2 - \sum_a \mathbf{u}_a^T \mathbf{u}_a \right\} \right]\]

これの\(\exp (\frac{1}{2} \tilde{q} (\sum_a \mathbf{u}_a)^2)\)にHubbard-Stratonovich変換を施すと

\[(3.18) = \int d\tilde{Q} \int d\tilde{q} \ \exp \left[ N \left( \frac{1}{2} n Q \tilde{Q} - \frac{1}{2} n (n-1) q \tilde{q}\right)\right] \exp \left( -\frac{1}{2} (\tilde{Q} + \tilde{q}) \sum_a \mathbf{u}_a^T \mathbf{u}_a \right) \times \int D_z \exp \left[ \sqrt{\tilde{q}} \mathbf{z} \sum_a \mathbf{u}_a \right]\]

これの全体に\(\prod_{a=1}^n \int {\bf{u}}_a\)を作用させれば、求めたかったエントロピーの計算をしたことになります。するとガウス積分より

\[\begin{align} S(Q) &= \frac{1}{N} \log \prod_a \int d{\bf{u}}_a \ \prod_{a, b} \delta \left( N q^{ab} - {\bf{u}}_a {\bf{u}}_b \right) \notag \\ &= \frac{1}{N} \log \int d\tilde{Q} \int d \tilde{q} \exp \left( N (\frac{n}{2} Q \tilde{Q} + \frac{n}{2} (n-1) q \tilde{q})\right) \left( \sqrt{\frac{2\pi}{\tilde{Q} + \tilde{q}}} \right)^{nN} \int D_z \exp \left( \frac{nN \tilde{q} z^2}{ 2(\tilde{Q} + \tilde{q})}\right) \tag{3.19} \end{align}\]

(3.19)式の\(\int D_z\)部分において、\(n \ll 1\)より

\[\int D_z \exp \left( \frac{nN \tilde{q} z^2}{ \tilde{Q} + \tilde{q}}\right) \simeq \int D_z \left( 1 + nN\frac{\tilde{q} z^2}{2(\tilde{Q} + \tilde{q})}\right) = 1 + n N \frac{\tilde{q}}{2 (\tilde{Q} + \tilde{q})} \simeq \exp \left( n N \frac{\tilde{q}}{2 (\tilde{Q}+\tilde{q})}\right)\]

さらに、\(n (n-1) \simeq -n\)などを用いると

\[S(Q) = \frac{1}{N} \log \int d\tilde{Q} \int d\tilde{q} \exp (nNh(Q)) \tag{3.20}\]

と整理できます。ここで

\[h(Q) = \frac{1}{2} (Q \tilde{Q} + q \tilde{q}) + \frac{1}{2} \log \left( \frac{2\pi}{\tilde{Q} + \tilde{q}}\right) + \frac{1}{2} \frac{\tilde{q}}{\tilde{Q} + \tilde{q}} \tag{3.21}\]

積分部分に鞍点法を用います。

\[\frac{\partial h}{\partial \tilde{Q}} = \frac{1}{2} Q - \frac{1}{2} \frac{1}{\tilde{Q} + \tilde{q}} - \frac{1}{2} \frac{\tilde{q}}{(\tilde{Q}+\tilde{q})^2} = 0 \ \Longrightarrow \ Q = \frac{1}{\tilde{Q} + \tilde{q}} + \frac{\tilde{q}}{(\tilde{Q} + \tilde{q})^2} \tag{3.22}\] \[\frac{\partial h}{\partial \tilde{q}} = \frac{1}{2} q - \frac{1}{2} \tilde{\tilde{q}}{\tilde{Q} + \tilde{q}} = 0 \ \Longrightarrow \ q = \frac{\tilde{q}}{\tilde{Q} + \tilde{q}} \tag{3.23}\]

分配関数の計算

\[[Z^n] = \int dQ \ \exp (N g(Q) + NS(Q))\] \[g(Q) = -\frac{\lambda}{2} \sum_a q^{aa} + \frac{1}{4} \sum_{a, b} (q^{ab})^2 \underbrace{=}_{レプリカ対称性} -\frac{\lambda}{2} n Q + \frac{1}{4} nQ^2 + \frac{1}{4} n(n-1) q^2\]

ここでも鞍点法を用います。

\[\frac{\partial }{\partial Q} (eの肩) = - \frac{\lambda}{2} + \frac{1}{2} Q + \frac{1}{2} \tilde{Q} = 0 \ \Longrightarrow \ \tilde{Q} = \lambda - Q \tag{3.24}\] \[\frac{\partial }{\partial q} (eの肩) = -\frac{1}{2} q + \frac{1}{2} \tilde{q} = 0 \ \Longrightarrow \ \tilde{q} = q \tag{3.25}\]

これらをまとめると

\[Q -q = \frac{1}{\lambda - (Q-q)} \tag{3.26}\] \[q = \frac{q}{(\lambda - (Q-q))^2} \tag{3.27}\]

(3.27)式から\(q = 0\), \(q \neq 0\)の2種類の解がありますが、重要なのは\(q = 0\)の方です。こちらを採用すると(3.26)式より

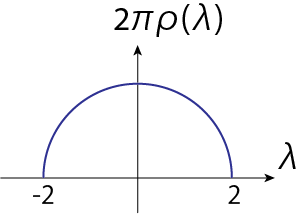
\[Q = \frac{1}{2} (\lambda \pm \sqrt{\lambda^2 - 4})\] \[\rho (\lambda) = -\frac{2}{\pi} \frac{\partial }{\partial \lambda} {\rm Im} (\log Z) = -\frac{2}{\pi} {\rm Im} \left( - \frac{1}{2} Q\right) = \frac{1}{\pi} {\rm Im} (Q) = \frac{1}{2\pi} \sqrt{4-\lambda^2} \ (-2 < \lambda < 2) \tag{3.28}\]

よって固有値分布が半円則を満たしていることがわかります。元を辿ると、\(Q\)はスピングラス秩序パラメータの対角成分でした。それは\(q^{ab} = \frac{1}{N} \sum_{i=1}^N u_{i, a} u_{i, b}\)からきているので、そもそもは\(u\)という人工的なスピン変数の大きさから決定されていることがわかります。

ウィグナーの半円則。

Marchenko-Pastur law

以下のような分布を考えます。

\[P (x_{\mu i}) = \left( \frac{1}{2\pi} \right)^{\frac{MN}{2}} \exp \left( - \frac{1}{2} x_{\mu i}^2\right) \tag{3.29}\]

この分布に従う\(x \in \mathbb{R}^{M \times N}\)を用いて以下の行列を作ります。

\[A_{ij} = \frac{1}{N} \sum_\mu x_{\mu i} x_{\mu j} \ \left( A = \frac{1}{N} X^T X \right) \tag{3.30}\]

この行列の固有値分布は

\[\rho (\lambda) = \frac{1}{N} \sum_{i=1}^N [\delta (\lambda - \lambda_i)]_A = \frac{1}{\pi} \frac{\partial}{\partial \lambda} {\rm Im} \frac{1}{N} [\log {\rm det}(\lambda I -A)]_A \tag{3.31}\]

先ほどと同じ考え方で、分配関数は

\[Z (\lambda) = \int d{\bf{u}} \exp \left( \frac{1}{2} {\bf{u}}^T (\lambda I -A) {\bf{u}} \right) = \sqrt{\frac{(2\pi)^N}{\rm{det}(\lambda I -A)}} \tag{3.32}\]

よって

\[[Z^n(\lambda)]_A = \prod_a \int d{\bf{u}}_a \exp \left( -\frac{\lambda}{2} \sum_a {\bf{u}}_a^T {\bf{u}} \right) \left[ \exp \left( \frac{1}{2} \sum_a {\bf{u}}_a^T A {\bf{u}}_a \right) \right]_A \tag{3.33}\]

ここで\(A\)の平均を計算する必要がありますが、(3.30)式の定義からそんな簡単に求めることはできません。

中心極限定理

ここで以下のように式変形をしましょう。

\[{\bf{u}}_a^T A {\bf{u}}_a = \frac{1}{N} \sum_\mu \sum_i \sum_j x_{\mu i} u_{i, a} x_{\mu j} u_{j, a} \tag{3.34}\]

ここで

\[y_{\mu a} \equiv \frac{1}{\sqrt{N}} \sum_{i=1}^N x_{\mu i} u_{i, a} \tag{3.35}\]

という量を定義します。すると

\[(3.34) = \sum_\mu y_{\mu a} y_{\mu a}\]

ここで中心極限定理を考えましょう。平均\(\mu\), 分散\(\sigma^2\)の乱数列\(x_1 \sim x_n\)があるとき、\(\sum_{k=1}^n \frac{x_k}{n}\)は平均\(\mu\), 分散\(\sigma^2/n\)のガウス分布になる、というものです。
よってここでは\(y_{\mu a}\)という変数において、その平均は\([y_{\mu a}]_x = 0\), そして分散は\([y_{\mu a} y_{\mu b}] = \frac{1}{N} \sum_{i=1}^N u_{ia} u_{ib} = q^{ab}\)となることが予想されます。

Equivalence theorem (等価定理)

上の予想から、\(x\)に関する平均の計算は\(y\)についての計算を考えてよく

\[\left[ f(\frac{1}{\sqrt{N}} \sum_{i=1}^N x_{\mu i} u_{ia} )\right]_x = \int d{\bf{y}}_\mu P ({\bf{y}}_\mu) \tag{3.36}\]

となります。これを等価定理と呼びます。これを用いると

\[\begin{align} [Z^n] &= \prod_a \int d {\bf{u}}_a \prod \left[ \int d{\bf{y}}_\mu P({\bf{y}}_\mu) \exp \left( \frac{1}{2} \sum_a y_{\mu a}^2 \right) \right] \notag \\ &\qquad \times \exp \left( - \frac{N \lambda}{2} \sum_a \frac{\mathbf{u}_a^T \mathbf{u}_a}{N} \right) \prod_{a, b} \delta \left( N q^{ab} - \mathbf{u}_a^T \mathbf{u}_b \right) \tag{3.37} \end{align}\]

後半のデルタ関数部分は、これまでやってきたものと同じエントロピーを表していることがわかります。

形が一緒なので、このリストを作っておいて、あとはコピペすれば大丈夫？問題設定・エネルギー関数が変わるのでそこだけ注意して議論を進めます。

統計物理学が情報に応用でき、同じ形で記述できるということがとても重要です。

すると

\[[Z^n (\lambda)] = \int dQ \exp (N g(Q) + N(Q)) \tag{3.38}\]

と書けることがわかります。エントロピー項は先ほどと格好が同じなので、以降はエネルギーを表す部分だけ計算を進めましょう。

エネルギー項

(3.37), (3.38)式より

\[g(Q) = \frac{1}{N} \sum_\mu \log \int d \mathbf{y}_\mu P (\mathbf{y}_\mu) \exp \left( \frac{1}{2} \sum_a y_{\mu a}^2 \right) - \frac{\lambda}{2} \sum_a q^{aa} \tag{3.39}\]

ここで、レプリカ対称性を仮定して、\(\sum_a q^{ab} = nQ\)とします。
次に(3.39)式の積分部分を計算しましょう。ここで\(y_{\mu a}\)の平均は0, 分散が\(q^{ab}\)になることを思い出しましょう。これに対応して変数\(x_a\)(平均0, 分散1)と変数\(z\)(平均0, 分散1)の2つを用意します。そしてこれらを用いて\(y_{\mu a}\)を以下のように書きましょう。

\[y_{\mu a} = \sqrt{q} z + \sqrt{Q-q} x_a \tag{3.40}\]

するとこの平均は

\[[y_{\mu a}]_{x, z} = 0\]

さらに分散は

\[[y_{\mu a} y_{\mu b}] = q[z^2] + C_1 [z x_a] + C_2 [z x_b] + (Q-q) [x_a x_b] = q + (Q-q) \delta_{ab}\]

となり、\(y_{\mu a}\)を再現することができます(ここで\(C_1, C_2\)は適当な係数です)。すると

\[g(Q) = \frac{1}{N} \sum_{\mu=1}^M \log \int D_z \left( \int D_x \exp \left( \frac{1}{2} (\sqrt{q} z + \sqrt{Q-q} x)^2 \right) \right)^n \tag{3.41}\]

\(e\)の肩だけ整理してみましょう。

\[-\frac{1}{2} (1-(Q-q)) \left( x - \frac{\sqrt{Q-q} \sqrt{q}z}{1-(Q-q)}\right)^2 + \frac{1}{2} \frac{(Q-q)qz^2}{1-(Q-q)} + \frac{1}{2}qz^2\]

これより、ガウス積分を行うと

\[\begin{align} g(Q) &= \frac{M}{N} \int D_z \left( \sqrt{\frac{2\pi}{1-(Q-z)}}\right)^n \exp \left( \frac{1}{2} \frac{nq z^2}{1-(Q-q)}\right) \notag \\ &\underbrace{\simeq}_{n \ll 1} -\frac{n \alpha}{2} \log (1-(Q-q)) + \frac{n\alpha}{2} \frac{q}{1-(Q-q)} - \frac{\lambda}{2} nQ \tag{3.42} \end{align}\]

ここで\(\alpha = M/N\)です。よって先ほど計算したエントロピーも用いて

\[\begin{align} [Z^n] &= \int dQ \int dq \exp \left[ N \left( -\frac{\lambda}{2} n Q- \frac{n\alpha}{2} \log(1-(Q-q)) + \frac{n \alpha}{2} \frac{q}{1-(Q-q)}\right) \right. \notag \\ & \left. \qquad + N \left( \frac{1}{2}n Q \tilde{Q} + \frac{1}{2} n q \tilde{q} - \frac{n}{2} \log (\tilde{Q} + \tilde{q}) + \frac{\tilde{q}}{2(\tilde{Q} + \tilde{q})}\right)\right] \tag{3.43} \end{align}\]

(3.43)式の\(e\)の肩の部分に鞍点法を用います。すると

\[Q = \frac{1}{\tilde{Q} + \tilde{q}}, \qquad q = \frac{\tilde{q}}{(\tilde{Q} + \tilde{q})^2} \tag{3.44}\] \[\begin{align} &\frac{\partial }{\partial Q} (eの肩) = -\frac{\lambda}{2} + frac{\alpha}{2} \frac{1}{1-(Q-q)} + \frac{\alpha}{2} \frac{q}{(1-(Q-q)^2)} + \frac{1}{2} \tilde{Q} = 0 \notag \\ &\Longrightarrow \ \tilde{Q} = \lambda - \frac{\alpha}{1-(Q-q)} - \frac{\alpha q}{(1-(Q-q))^2} \tag{3.45} \end{align}\] \[\begin{align} &\frac{\partial }{\partial \tilde{q}} (eの肩) = - \frac{\alpha}{2} \frac{1}{1-(Q-q)} + \frac{\alpha}{2} \frac{1}{1-(Q-q)} - \frac{\alpha}{2} \frac{q}{(1-(Q-q))^2} + \frac{1}{2} \tilde{q} = 0 \notag \\ &\Longrightarrow \ \tilde{q} = \frac{\alpha q}{(1-(Q-q))^2} \tag{3.46} \end{align}\]

(3.44), (3.46)式から\(q= 0\)と\(q \neq 0\)の解があることがわかりますが、ここでは\(q = 0\)を選択します。\(q = \tilde{q} = 0\)より

\[\tilde{Q} = \lambda - \frac{\alpha}{1-Q}, \qquad Q = \frac{1}{\tilde{Q}} \ \Longrightarrow \ \therefore \ Q = \frac{1}{2\lambda} (\lambda + (1-\alpha) \pm i \sqrt{4\alpha - (\lambda-(\alpha+1))^2}) \tag{3.47}\]

これの虚数部分が固有値分布を表していることがわかります。\(\alpha\)によって固有値分布が変わる、これをMarchenko-Pastur則と呼びます。

Appendix A: 行列のトレースの公式 (3.3)式の証明

途中で出てきた行列のトレースについて成り立つ公式を証明しましょう。そのために以下の手順で示していきます。

可換則

\[\mathrm{Tr} (AB) = \sum_{i=1}^n (AB)_{ii} = \sum_{i=1}^n \left( \sum_{j=1}^n A_{ij} B_{ji} \right) = \sum_{j=1}^n \left( \sum_{i=1}^n B_{ji} A_{ij} \right) = \mathrm{Tr} (BA) \tag{A.1}\]

が成り立ちます。

行列のトレースが、その行列の固有値の総和となる

行列\(A\)を対角化するために用いる正則行列を\(\Lambda\)とすると

\[\Lambda^{-1} A \Lambda = C \tag{A.2}\]

右辺の\(C\)は\(A\)を対角化して生まれた対角行列です。\(A\)の固有値を\(\lambda_1, \lambda_2, \cdots, \lambda_n\)とすると

\[C = \left( \begin{array}{cccc} \lambda_1 & & & \mathbf{0} \\ & \lambda_2 & & \\ & & \ddots & \\ \mathbf{0} & & & \lambda_n \end{array} \right) \tag{A.3}\]

です。(A.2)の両辺のトレースを取ると

\[\mathrm{Tr} (\Lambda^{-1} A \Lambda) = \mathrm{Tr} (C) = \sum_{i=1}^n \lambda_i\]

一方で上式の最左辺は、先ほどの(A.1)式を用いて

\[\mathrm{Tr} (\Lambda^{-1} A \Lambda) = \mathrm{Tr} ( A \Lambda^{-1} \Lambda) = \mathrm{Tr} (A)\]

です。以上を合わせて

\[\mathrm{Tr} (A) = \sum_{i=1}^n \lambda_i \tag{A.4}\]

途中の公式の証明

これらから、求める形の証明をしましょう。(A.2)式より

\[A = \Lambda C \Lambda^{-1} \ \Longrightarrow \ e^A = e^{\Lambda C \Lambda^{-1}}\]

定義に従って、これの右辺を和の形で表現すると

\[e^{\Lambda C \Lambda^{-1}} = I + \Lambda C \Lambda^{-1} + \frac{(\Lambda C \Lambda^{-1})}{2!} + \cdots\]

となります。ここで\((\Lambda C \Lambda^{-1}) = \Lambda C \Lambda^{-1}\Lambda C \Lambda^{-1} = \Lambda C^2 \Lambda^{-1}\)などより

\[e^{\Lambda C \Lambda^{-1}} = \Lambda \Lambda^{-1} + \Lambda C \Lambda^{-1} + \frac{\Lambda C^2 \Lambda^{-1}}{2!} + \cdots = \Lambda \left( I + C + \frac{C^2}{2!} + \cdots \right) \Lambda^{-1} = \Lambda e^C \Lambda^{-1}\]

よって

\[e^A = \Lambda e^C \Lambda^{-1} \ \Longrightarrow \ \mathrm{det} (e^A) = \mathrm{det} (\Lambda e^C \Lambda^{-1}) = \mathrm{det} (\Lambda) \mathrm{det} (e^C) \mathrm{det} (\Lambda^{-1}) = \mathrm{det} (e^C)\]

となります。ここで(A.3)式より

\[e^C = I + C + \frac{C^2}{2!} + \cdots = \left( \begin{array}{cccc} 1 + \lambda_1 + \frac{\lambda_1^2}{2!} + \cdots & & & \\ & 1 + \lambda_2 + \frac{\lambda_2^2}{2!} + \cdots & & \\ & & \ddots & \\ & & & 1 + \lambda_n + \frac{\lambda_n^2}{2!} + \cdots \end{array} \right) = \left( \begin{array}{cccc} e^{\lambda_1} & & & \\ & e^{\lambda_2}& & \\ & & \ddots & \\ & & & e^{\lambda_n} \end{array} \right)\]

とわかるので

\[\mathrm{det} (e^C) = e^{\lambda_1} e^{\lambda_2} \cdots e^{\lambda_n} = e^{\lambda_1 + \lambda_2 + \cdots + \lambda_n} \underbrace{=}_{(A.4)} e^{\mathrm{Tr} (A)} \ \Longrightarrow \ \therefore \ \mathrm{det} (e^A) = e^{\mathrm{Tr} (A)} \tag{A.5}\]

が成立することがわかります。(A.5)式の両辺のlogを取ると

\[\log [\mathrm{det} (e^A)] = \mathrm{Tr} (A)\]

そして\(A = A\log e = \log e^A\)を用いれば

\[\log [\mathrm{det} (e^A)] = \mathrm{Tr} [\log e^{A}]\]

となります。両辺に\(e^A\)が現れているので、\(e^A \rightarrow \lambda I - A\)のように置き換えれば、(3.3)式に一致します。

Appendix B: 途中の予想が正しいことの証明

\[P(y_\mu^{a=1 \sim n}) = \int_{-\infty}^\infty \prod_{i=1}^N dx_{\mu i} \exp \left( - \frac{1}{2} \sum_{i=1}^N x_{\mu i}^2 \right) \prod_{a=1}^n \delta \left( y_\mu^a - \frac{1}{\sqrt{N}} \sum_{i=1}^N x_{\mu i} u_{ia} \right)\]

デルタ関数のフーリエ積分表示を用いると

\[P(y_\mu^{a=1 \sim n}) = \int_{-\infty}^\infty d\tilde{y}_\mu \int d{\bf{x}}_\mu \exp \left( -\frac{1}{2} \sum_{i=1}^N x_{\mu i}^2 + i \sum_{a=1}^n \tilde{y}_{\mu a} \left( y_{\mu a} - \frac{1}{\sqrt{N}} \sum_{i=1}^N x_{\mu i} u_{ia} \right) \right)\]

この式に現れた\(e\)の肩について整理しましょう。

\[-\frac{1}{2} \sum_{i=1}^N \left( x_{\mu i} - i \sum_a \frac{\tilde{y}_{\mu a}}{\sqrt{N}} u_{ia} \right)^2 - \frac{1}{2N} \sum_{i=1}^N \left( \sum_{a=1}^n \tilde{y}_{\mu a} u_{ia}\right)^2 + i \sum_a y_{\mu a} \tilde{y}_{\mu a}\]

よってガウス積分ができて

\[P(y_\mu^{a=1 \sim n}) \propto \int d\tilde{y}_{\mu a} \exp \left( -\frac{1}{2} \sum_{a, b} \tilde{y}_{\mu a} \left( \frac{1}{N} \sum_{i=1} u_{ia} u_{ib}\right) \tilde{y}_{\mu b} + i \sum_{a=1}^n \tilde{y}_{\mu a} y_{\mu a} \right) \propto \exp \left( - \frac{1}{2} \sum_{a, b} y_{\mu a} [Q^{-1}]_{a b} y_{\mu b} \right)\]

となります。よって\(y_{\mu a}\)が再びガウス分布に従っていることがわかります。ここから平均は\([y_{\mu a}] = 0\), 分散は\([y_{\mu a} y_{\mu b}] = [Q]_{ab} = q^{ab}\)となることがわかりました。