Table of contents
電子による熱伝導
ここでは、電子による熱伝導効果が恒星のエネルギー輸送に与える影響を考えましょう。 温度勾配が存在すると、ある面を通過するガス粒子のエネルギーは、温度の高い側から来るもののほうが大きくなります。 よって、ガス粒子の熱運動によってエネルギーが流れることになります。 これが粒子による熱伝導です。
電子の熱伝導が重要となる状況
電離ガス中では、イオンに比べて電子の方が素早く飛び交っているため、熱伝導はもっぱら電子によって起こります。 しかし一般には輻射によるエネルギー輸送の方が、電子による熱伝導に比べて格段に効率が良いことが知られています。 これは、通常は光子の平均自由行程に比べて非常に長いためです。 しかし、太陽コロナのように高温かつ稀薄なガスでは電子の熱伝導が重要となり、コロナ内は電子の熱伝導の働きでほぼ等温に保たれています。 また逆に、ガス密度が非常に大きく電子が縮退している状態では、空いている電子のエネルギー状態が少なくなります。 これにより電子の衝突確率が減少し、平均自由行程が長くなります。 よって電子が縮退した高密度状態では、輻射によるエネルギー輸送よりも電子熱伝導によるエネルギー輸送の方が卓越しています。 このため白色矮星内部は、効率の良い電子熱伝導によりほぼ等温に保たれているとされています。
熱伝導の不透明度定式化
熱伝導係数を\(k_c\)とすると、熱伝導によるエネルギー流束\(F_\mathrm{cond}\)は
\[F_\mathrm{cond} = - k_c \frac{dT}{dr} \tag{5.3.1}\]と書かれます。 \(F_\mathrm{cond}\)は輻射によるエネルギー流束(5.1.16)式と同様に、温度勾配に比例するため、熱伝導に対する不透明度(conductive opacity) \(\kappa_\mathrm{cond}\)を
\[\kappa_\mathrm{cond} = \frac{4ac T^3}{3\rho k_c} \tag{5.3.2}\]のように定義しましょう。 すると、輻射と熱伝導両方によるエネルギー流束は
\[F_\mathrm{rad} + F_\mathrm{cond} = - \left( \frac{1}{\kappa} + \frac{1}{\kappa_\mathrm{cond}} \right) \frac{4ac}{3\rho} T^3 \frac{dT}{dr} \tag{5.3.3}\]と表すことができます。
\(T=10^7\)Kの場合の熱伝導不透明度\(\kappa_\mathrm{cond}\)を、次の図に示します。
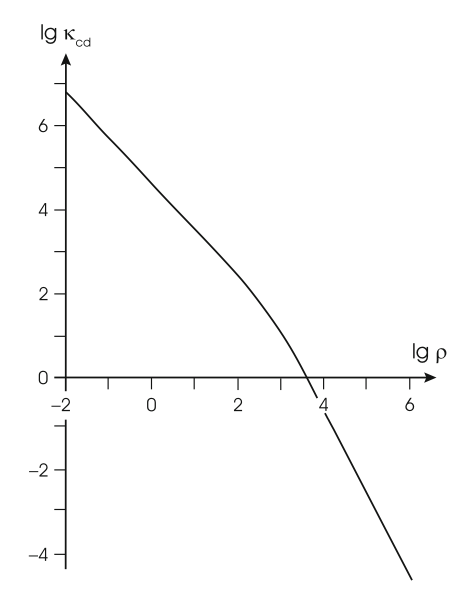
密度が大きいほど小さな値を持つようになり、熱伝導が需要になります。 そのため、熱伝導の効果は主系列星の内部では非常に小さいですが、進化の進んだ星の中心部に実現される非常に高密度の状態では、輻射よりも効率が良くなります。 温度が大きいほどグラフが左側にシフトしていき、同じ密度でもより\(\kappa_\mathrm{cond}\)の値が小さくなります。
そして次の図は、密度-温度図上の各領域で、どの吸収がロスランド平均不透明度に重要であるかを表したものです。
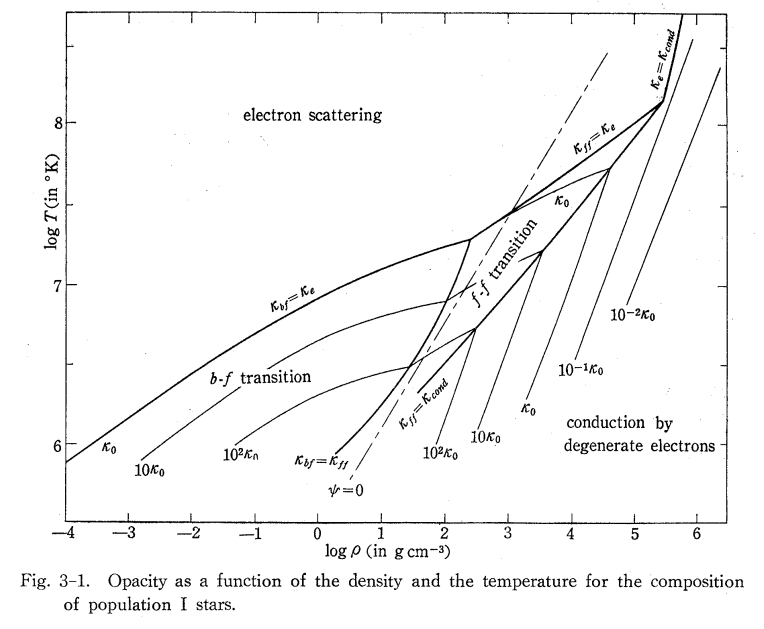
高温かつ低密度(図の左上)では電子散乱が重要で、低温かつ高密度(図の右下)では電子熱伝導が需要となります。 この図で\(\psi\)と記されている量は、こちらのページの\(\eta\)と同じもので、電子の縮退の程度を表す量です。 \(\psi=0\)の線よりも高密度側で電子の縮退が需要となります。
参考文献
[1] Kippenhahn, Weigert & Weiss, “Stellar Structure and Evolution”
[2] Hayashi et al, 1962, “Evolution of the Stars”
[3] 高原文郎, “宇宙物理学”
[4] 野本憲一, 定金晃三, 佐藤勝彦, “恒星”