Table of contents

1. HLLC法
   1. 流体方程式群
   2. 流束計算
   3. 数値計算に用いる
   4. 磁気流体方程式への拡張
      1. \(B_x = 0\)の場合
      2. \(B_x \neq 0\)の場合、Gurskiの手法
      3. \(B_x \neq 0\)の場合、Liの方法
   5. HLLC流束の計算モジュール
2. 参考文献

HLLC法

ここでは(磁気)流体力学の計算手法であるHLLC法についての勉強メモを記述しています。

流体方程式群

いきなり磁場がある場合は難しいため、最初は磁場のない流体を考えることにしましょう。簡単のため1次元系を解くことにします。すると解きたい方程式は

\[\frac{\partial}{\partial t} \left( \begin{array}{c} \rho \\ \rho v_x \\ \rho v_y \\ \rho v_z \\ E \end{array} \right) + \frac{\partial}{\partial x} \left( \begin{array}{c} \rho v_x \\ \rho v_x v_x + P \\ \rho v_y v_x \\ \rho v_z v_x \\ (E + P) v_x \end{array}\right) = \frac{\partial \mathbf{U}}{\partial t} + \frac{\partial \mathbf{F}}{\partial x} = \mathbf{0} \tag{1}\]

のように書かれます。

流束計算

HLL (Harten-Lax-van Leer)法は、中間状態を1つであると仮定しました。今回は中間状態を下図のように2つとして計算を行います。

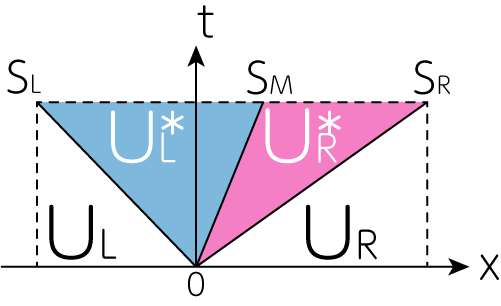
ただし、中間状態において、\(x\)方向の流体の速度は一定であるとします。すなわち

\[v_{x, L}^\ast = v_{x, R}^\ast = S_M \tag{2}\]

この\(S_M\)は中間状態を代表する速度です。よってHLLの中間状態

\[\mathbf{U}_\mathrm{HLL}^\ast = \frac{S_R \mathbf{U}_R - S_L \mathbf{U}_L - \mathbf{F}_R + \mathbf{F}_L}{S_R - S_L} \tag{3}\]

から導出されるだろうと考えることができます。

\[\rho_\mathrm{HLL}^\ast = \frac{S_R \rho_R - S_L \rho_L - \rho_R v_{x, R} + \rho_L v_{x, L}}{S_R - S_L}\] \[(\rho v_x)_\mathrm{HLL}^\ast = \frac{S_R \rho_R v_{x, R} - S_L \rho_L v_{x, L} - (\rho_R v_{x, R} v_{x, R} + P_R) + (\rho_L v_{x, L} v_{x, L} + P_L)}{S_R - S_L}\]

以上より

\[S_M = \frac{(\rho v_x)_\mathrm{HLL}^\ast}{\rho_\mathrm{HLL}^\ast} = \frac{(S_R - v_{x, R}) \rho_R v_{x, R} - (S_L - v_{x, L}) \rho_L v_{x, L} - P_R + P_L}{(S_R - v_{x, R})\rho_R - (S_L-v_{x, L}) \rho_L} \tag{4}\]

と求まります。次に中間状態の圧力を考えましょう。\(S_\alpha \ (\alpha = L, R)\)の速度で進む波面でのジャンプ条件より

\[S_\alpha \mathbf{U}_\alpha^\ast - \mathbf{F}_\alpha^\ast = S_\alpha \mathbf{U}_\alpha - \mathbf{F}_\alpha \tag{5}\]

です。この式と(1)式の第1式(連続の式)を考えると

\[S_\alpha \rho_\alpha^\ast - \rho_\alpha^\ast v_{x, \alpha}^\ast = S_\alpha \rho_\alpha - \rho_\alpha v_{x, \alpha} \ \underbrace{\Longrightarrow}_{(2)} \ \rho_\alpha^\ast = \rho_\alpha \frac{S_\alpha - v_{x, \alpha}}{S_\alpha - S_M} \tag{6}\]

続いて(5)式と(1)式の第2式(\(x\)方向の運動量保存式)を考えると

\[\begin{aligned} &S_\alpha \rho_\alpha^\ast v_{x, \alpha}^\ast - (\rho_\alpha^\ast v_{x, \alpha}^\ast v_{x, \alpha}^\ast + P_\alpha^\ast) = S_\alpha \rho_\alpha v_{x, \alpha} - (\rho_\alpha v_{x, \alpha} v_{x, \alpha} + P_\alpha) \\ &\underbrace{\Longrightarrow}_{(2)} \ \rho_\alpha^\ast S_M (S_\alpha - S_M) - P_\alpha^\ast = \rho_\alpha v_{x, \alpha} (S_\alpha - v_{x, \alpha}) - P_\alpha \end{aligned}\]

ここに(6)式を用いれば

\[\rho_\alpha S_M (S_\alpha - v_{x, \alpha}) - P_\alpha^\ast = \rho_\alpha v_{x, \alpha} (S_\alpha - v_{x, \alpha}) - P_\alpha \ \Longrightarrow \ P_\alpha^\ast = P_\alpha + \rho_\alpha (S_\alpha - v_{x, \alpha}) (S_M - v_{x, \alpha}) \tag{7}\]

を得ます。実は衝撃波管の物理から、\(S_M\)を挟んで

\[P_L^\ast = P_R^\ast = P^\ast \tag{8}\]

が成り立ちます。これは\(\rho_L^\ast \neq \rho_R^\ast\)でありながら圧力は同じ値でバランスしている接触不連続面であることを意味します。
同様に(1)式の第3式(\(y\)方向の運動量保存式)より

\[S_\alpha \rho_\alpha^\ast v_{y, \alpha}^\ast - \rho_\alpha^\ast v_{y, \alpha}^\ast v_{x, \alpha}^\ast = S_\alpha \rho_\alpha v_{y, \alpha} - \rho_\alpha v_{y, \alpha} v_{x, \alpha} \ \underbrace{\Longrightarrow}_{(2)} \ \rho_\alpha^\ast v_{y, \alpha}^\ast (S_\alpha - S_M) = \rho_\alpha v_{y, \alpha} (S_\alpha - v_{x, \alpha})\]

ここに(6)式を用いることで

\[v_{y, \alpha}^\ast = v_{y, \alpha} \tag{9}\]

を得ます。同様に

\[v_{z, \alpha}^\ast = v_{z, \alpha} \tag{10}\]

も導くことができます。最後に(1)式と第5式(エネルギー保存式)より

\[S_\alpha E_\alpha^\ast - (E_\alpha^\ast + \underbrace{P_\alpha^\ast}_{(8)}) \underbrace{v_{x, \alpha}^\ast}_{(2)} = S_\alpha E_\alpha - (E_\alpha + P_\alpha) v_{x, \alpha} \ \Longrightarrow \ E_\alpha^\ast = \frac{(S_\alpha - v_{x, \alpha}) E_\alpha - P_\alpha v_{x, \alpha} + P^\ast S_M}{S_\alpha - S_M} \tag{11}\]

となります。これらをまとめて

\[\mathbf{F}_\alpha^\ast = \left( \begin{array}{c} \rho_\alpha^\ast S_M \\ \rho_\alpha^\ast S_M S_M + P^\ast \\ \rho_\alpha^\ast v_{y, \alpha}^\ast S_M \\ \rho_\alpha^\ast v_{z, \alpha}^\ast S_M \\ (E_\alpha^\ast + P^\ast) S_M \end{array}\right) \tag{12}\]

とすることで、求めたかった中間状態の流束を計算することができます。途中で出てきたように、HLLC法は接触不連続面の波の速度\(S_M\)およびそれを境に物理量の変化が起こることを考慮しています。 HLLCの”C”は、HLLを改良し接触不連続面(contact discontinuity)も捉えられるようにしたことから来るものです。

数値計算に用いる

HLL法と同様に、実際の数値計算では\(S_L, S_M, S_R\)の大きさを考慮する必要があります。HLLのときと同様に考えましょう。下図は左上から順に\(S_L > 0, S_L \leq 0 < S_M, S_M \leq 0 <S_R, S_R \leq 0\)の場合を図示したものです。

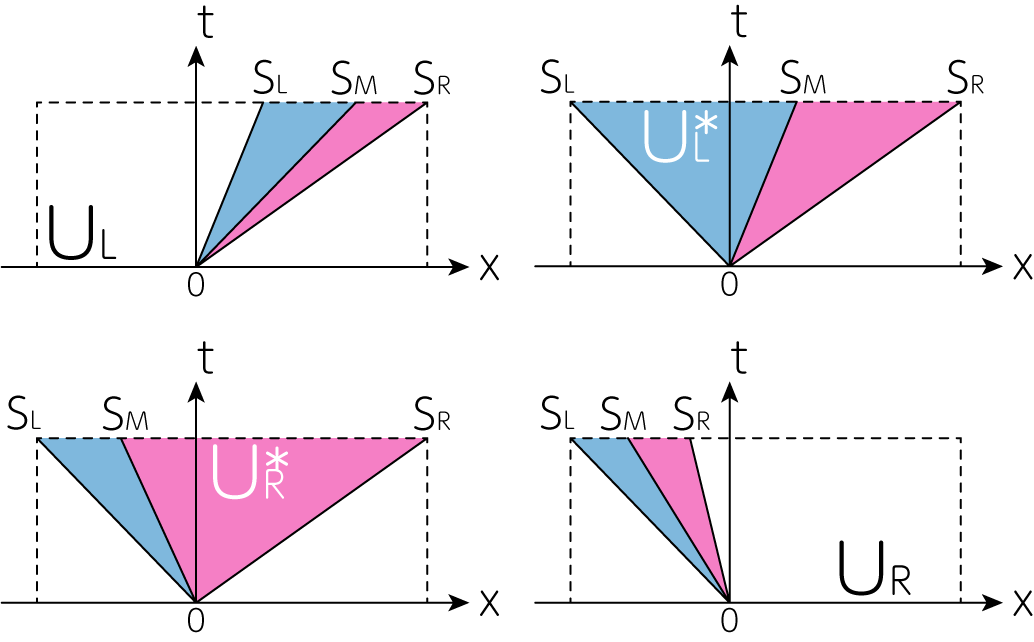
以上より、数値計算を行う場合、その流束の選択は

\[\mathbf{F}_\mathrm{HLLC} = \left\{ \begin{array}{ll} \mathbf{F}_L & \mathrm{if} \ S_L > 0 \\ \mathbf{F}_L^\ast & \mathrm{if} \ S_L \leq 0 < S_M \\ \mathbf{F}_R^\ast & \mathrm{if} \ S_M \leq 0 < S_R \\ \mathbf{F}_R & \mathrm{if} \ S_R \leq 0 \end{array}\right. \tag{13}\]

磁気流体方程式への拡張

ここまでは磁場のない、流体方程式の場合のHLLCをご紹介してきました。ここからは磁場を含めた、より複雑な方程式についてのHLLC法を考えましょう。磁気流体方程式は

\[\frac{\partial}{\partial t} \left( \begin{array}{c} \rho \\ \rho v_x \\ \rho v_y \\ \rho v_z \\ E \\ B_x \\ B_y \\ B_z \end{array} \right) + \frac{\partial}{\partial x} \left( \begin{array}{c} \rho v_x \\ \rho v_x v_x + P_\mathrm{tot} - B_x^2 \\ \rho v_y v_x - B_y B_x\\ \rho v_z v_x - B_z B_x\\ (E + P_\mathrm{tot}) v_x - (\mathbf{B} \cdot \mathbf{v}) B_x \\ 0 \\ B_y v_x - v_y B_x \\ B_z v_x - v_z B_x \end{array}\right) = \frac{\partial \mathbf{U}}{\partial t} + \frac{\partial \mathbf{F}}{\partial x} = \mathbf{0} \tag{14}\]

です。それでは導出を始めましょう。HLL法と同様に\(S_L, S_R\)を最も速度の大きい磁気音波から求めます。 今は一次元系を考えているため、(14)式と\(\nabla \cdot \mathbf{B} = \frac{\partial B_x}{\partial x} = 0\)から、\(B_x\)は時間・空間に依存せず、一定・一様の値を持ちます。すなわち

\[B_{x, L} = B_{x, L}^\ast = B_{x, R}^\ast = B_{x, R} \tag{15}\]

のように考えることができます。(14)式の第二式(\(x\)方向の運動量保存則)と、\(S_\alpha \ (\alpha = L, R)\)で進行する波面のジャンプ条件(5)式より

\[S_\alpha \rho_\alpha^\ast v_{x, \alpha}^\ast - (\rho_\alpha^\ast v_{x, \alpha}^\ast v_{x, \alpha}^\ast + P_\mathrm{tot, \alpha}^\ast - (B_{x, \alpha}^\ast)^2) = S_\alpha \rho_\alpha v_{x, \alpha} - (\rho_\alpha v_{x, \alpha} v_{x, \alpha} + P_\mathrm{tot, \alpha} - B_{x, \alpha}^2)\]

(15)式から\(B_{x, \alpha}^\ast = B_{x, \alpha}\)です。従って、得られる関係式は(7)式において\(P \rightarrow P_\mathrm{tot}\)に置換したものに等しくなります。

\[P_{\mathrm{tot}, \alpha}^\ast = P_{\mathrm{tot}, \alpha} + \rho_\alpha (S_\alpha - v_{x, \alpha}) (S_M - v_{x, \alpha}) \tag{16}\]

そして\(S_M\)で進む波は接触不連続面を形成することから、全圧力は釣り合っているために

\[P_{\mathrm{tot}, L}^\ast = P_{\mathrm{tot}, R}^\ast = P_\mathrm{tot}^\ast \tag{17}\]

となります。

\(B_x = 0\)の場合

まずは簡単のため\(B_x = 0\)の場合について導出しましょう。このとき、磁気流体方程式は

\[\frac{\partial}{\partial t} \left( \begin{array}{c} \rho \\ \rho v_x \\ \rho v_y \\ \rho v_z \\ E \\ B_x \\ B_y \\ B_z \end{array} \right) + \frac{\partial}{\partial x} \left( \begin{array}{c} \rho v_x \\ \rho v_x v_x + P_\mathrm{tot}\\ \rho v_y v_x\\ \rho v_z v_x\\ (E + P_\mathrm{tot}) v_x \\ 0 \\ B_y v_x\\ B_z v_x \end{array}\right) = \mathbf{0} \tag{18}\]

のようになります。\(\rho v_y, \rho v_z\)の流束は(1)式と同じ形となるため、得られる中間状態量も同じです。よって

\[v_{y, \alpha}^\ast = v_{y, \alpha} , \quad v_{z, \alpha}^\ast = v_{z, \alpha} \tag{19}\]

を得ます。(18)式の第七式に対する\(S_\alpha\)で進行する波面でのジャンプ条件より

\[S_\alpha B_{y, \alpha}^\ast - B_{y, \alpha}^\ast \underbrace{v_{x, \alpha}^\ast}_{(2)} = S_\alpha B_{y, \alpha} - B_{y, \alpha} v_{x, \alpha} \ \Longrightarrow \ B_{y, \alpha}^\ast = \frac{S_\alpha - v_{x, \alpha}}{S_\alpha - S_M} B_{y, \alpha} \tag{20}\]

同様に(18)式の第八式から

\[B_{z, \alpha}^\ast = \frac{S_\alpha - v_{x, \alpha}}{S_\alpha - S_M} B_{z, \alpha} \tag{21}\]

が求まります。最後に(18)式の第五式から、同様のジャンプ条件を求めましょう。これは実は(11)式で\(P \rightarrow P_\mathrm{tot}\)としたものに等しく

\[E_\alpha^\ast = \frac{(S_\alpha - v_{x, \alpha}) E_\alpha - P_{\mathrm{tot}, \alpha} v_{x, \alpha} + P_\mathrm{tot}^\ast S_M}{S_\alpha - S_M} \tag{22}\]

と求まります。

\(B_x \neq 0\)の場合、Gurskiの手法

それでは\(B_x \neq 0\)の一般の場合のHLLC法を導出しましょう。先程の\(B_x =0\)の場合とは流束が異なるため、再定式化が必要となることは容易にわかります。 しかも\(S_M\)の速度で伝播する接触不連続面では、左右の速度・磁場の接戦成分(\(v_y, v_z, B_y, B_z\))は連続でなければなりません。 そのリーズナブルな求め方としては、(4)式のようにHLL中間状態を用いる方法があります。よって

\[v_{y, L}^\ast = v_{y, R}^\ast = \frac{(\rho v_y)_\mathrm{HLL}^\ast}{\rho_\mathrm{HLL}^\ast} \equiv v_y^\ast , \quad v_{z, L}^\ast = v_{z, R}^\ast = \frac{(\rho v_z)_\mathrm{HLL}^\ast}{\rho_\mathrm{HLL}^\ast} \equiv v_z^\ast \tag{23}\] \[B_{y, L}^\ast = B_{y, R}^\ast = B_{y, \mathrm{HLL}}^\ast, \quad B_{z, L}^\ast = B_{z, R}^\ast = B_{z, \mathrm{HLL}}^\ast \tag{24}\]

これらが求まっていれば、エネルギーを求めることができます。(14)式の第五式より

\[\begin{align} &S_\alpha E_\alpha^\ast - \{ (E_\alpha^\ast + P_\mathrm{tot}^\ast) S_M - (\mathbf{B}_\alpha^\ast \cdot \mathbf{v}_\alpha^\ast) B_x\} = S_\alpha E_\alpha - \{ (E_\alpha + P_{\mathrm{tot}, \alpha}) v_{x, \alpha} - (\mathbf{B}_\alpha \cdot \mathbf{v}_\alpha) B_x\} \notag \\ &\Longrightarrow \ E_\alpha^\ast = \frac{(S_\alpha - v_{x, \alpha}) E_\alpha - P_{\mathrm{tot}, \alpha} v_{x, \alpha} + P_\mathrm{tot}^\ast S_M + (\mathbf{B}_\alpha \cdot \mathbf{v}_\alpha - \mathbf{B}_\alpha^\ast \cdot \mathbf{v}_\alpha^\ast) B_x}{S_\alpha - S_M} \tag{25} \end{align}\]

これらがわかれば、あとは\(\mathbf{U}_\alpha^\ast = (\rho_\alpha^\ast, \rho_\alpha^\ast S_M, \rho_\alpha^\ast v_y^\ast, \rho_\alpha^\ast v_z^\ast, E_\alpha^\ast, B_x, B_{y, \mathrm{HLL}}^\ast, B_{z, \mathrm{HLL}}^\ast)\)として、(5)式から

\[\mathbf{F}_\alpha^\ast = \mathbf{F}_\alpha + S_\alpha (\mathbf{U}_\alpha^\ast - \mathbf{U}_\alpha) \tag{26}\]

のようにして\(\mathbf{F}_L^\ast, \mathbf{F}_R^\ast\)を求めることができます。このようにして\(B_x \neq 0\)でのHLLC流束を計算することが可能です。このように定める方法を、開発したGurskiの頭文字をとって、以降ではHLLC-Gと呼ぶことにします。 しかし、実はHLLC-Gには問題があります。それは\(B_x \rightarrow 0\)の極限を取ったときに、(23), (24)式が(19), (20), (21)式に一致しないことです。このことから、アルヴェーン波と遅い磁気音波衝撃波を正しく計算することができません(どうしても鈍った結果となります)。ただしそれ以外の、孤立した速い磁気音波衝撃波や接触不連続面は正しく分解して計算することができます。

\(B_x \neq 0\)の場合、Liの方法

別の方法がLiにより示されています。この手法を以降ではHLLC-Lと呼ぶことにします。HLLC-Gでは(23), (24)式のように\(v_{y, \alpha}^\ast, v_{z, \alpha}^\ast\)にHLL中間状態を用いていました。これにより\(B_x \rightarrow 0\)で一致しない問題が起こっていたのです。よってこれを解消するために、(18)式の第三式(\(y\)方向の運動量保存則)から、\(S_\alpha\)で進行する波面についてジャンプ条件を導いてみましょう。

\[\begin{align} &S_\alpha \rho_\alpha^\ast v_{y, \alpha}^\ast - (\rho_\alpha^\ast v_{y, \alpha}^\ast \underbrace{v_{x, \alpha}^\ast}_{(2)} - \overbrace{B_{y, \alpha}^\ast}^{(24)} B_x) = S_\alpha \rho_\alpha v_{y, \alpha} - (\rho_\alpha v_{y, \alpha} v_{x, \alpha} - B_{y, \alpha} B_x) \notag \\ &\Longrightarrow \ \frac{\overbrace{\rho_\alpha^\ast}^{(6)} (S_\alpha - S_M)}{\rho_\alpha (S_\alpha - v_{x, \alpha})} v_{y, \alpha}^\ast = v_{y, \alpha} + \frac{B_x (B_{y, \alpha}-B_{y, \alpha}^\ast)}{\rho_\alpha (S_\alpha - v_{x, \alpha})} \notag \\ &\Longrightarrow \ v_{y, \alpha}^\ast = v_{y, \alpha} + \frac{B_x (B_{y, \alpha}-B_{y, \alpha}^\ast)}{\rho_\alpha (S_\alpha - v_{x, \alpha})} \tag{27} \end{align}\]

同様に(18)式の第四式(\(z\)方向の運動量保存則)からは

\[v_{z, \alpha}^\ast = v_{z, \alpha} + \frac{B_x (B_{z, \alpha}-B_{z, \alpha}^\ast)}{\rho_\alpha (S_\alpha - v_{x, \alpha})} \tag{28}\]

が求まります。HLLC-Lはその求め方からわかるように、リーマンファン内で保存則を満たす手法です。さらにこの手法は\(B_x \rightarrow 0\)としたときに(27), (28)式は(19)式を再現できます。 しかし、万能というわけではありません。この手法には\(S_M\)に対する考察が含まれていないことから、接触不連続面でのジャンプ条件が保証されていません。 よってHLLC-Lでは、HLLC-Gではちゃんと計算されていた接触不連続面が正しく分解できないことがあります。さらに(24)式はそのまま用いているため、\(B_y^\ast, B_z^\ast\)に関しては\(B_x \rightarrow 0\)の極限で一致しない問題が残ります。

HLLC流束の計算モジュール

以下にHLLC-G流束計算コードのJulia実装例を示します。

using LinearAlgebra    
include("../convert/convert.jl")
include("../const/const.jl")
function hllcg!(F::Array{Float64, 2}, Vl::Array{Float64, 2}, Vr::Array{Float64, 2}, nxmax::Int64)
    for i in 1:nxmax-1
        rol = Vl[1, i]
        vnl = Vl[2, i]
        vtl = Vl[3, i]
        vul = Vl[4, i]
        prl = Vl[5, i]
        bnl = Vl[6, i]
        btl = Vl[7, i]
        bul = Vl[8, i]
        ror = Vr[1, i]
        vnr = Vr[2, i]
        vtr = Vr[3, i]
        vur = Vr[4, i]
        prr = Vr[5, i]
        bnr = Vr[6, i]
        btr = Vr[7, i]
        bur = Vr[8, i]
        # compute B * B of left side
        bl2 = dot(Vl[6:8, i], Vl[6:8, i])
        # compute v * B of left side
        vlbl = dot(Vl[2:4, i], Vl[6:8, i])
        # convert Vl ---> Ul
        Ul = Convert.v_to_u(Vl[:, i])
        # convert Ul, VL ---> Fl
        Fl = Convert.uv_to_f(Ul, Vl[:, i], bl2, vlbl)
        # compute B * B of right side
        br2 = dot(Vr[6:8, i], Vr[6:8, i])
        # compute v * B of right side
        vrbr = dot(Vr[2:4, i], Vr[6:8, i])
        # convert Vr ---> Ur
        Ur = Convert.v_to_u(Vr[:, i])
        # convert Ur, Vr ---> Fr
        Fr = Convert.uv_to_f(Ur, Vr[:, i], br2, vrbr)
        # compute fast-mode speed of left side
        gmprl = gm * prl
        vfl = sqrt(((bl2+gmprl)+sqrt((bl2+gmprl)^2-4*gmprl*bnl^2))/(2*rol))
        # compute fast-mode speed of right side
        gmprr = gm * prr
        vfr = sqrt(((br2+gmprr)+sqrt((br2+gmprr)^2-4*gmprr*bnr^2))/(2*ror))
        # compute sl, sr
        sl = min(vnl, vnr) - max(vfl, vfr)
        sr = max(vnl, vnr) + max(vfl, vfr)
        # compute HLL state U*
        Ui = (sr*Ur-sl*Ul-Fr+Fl) / (sr-sl)
        # compute sm(=vn), vt, vu, bn, bt, bu of intermediate states
        sm = Ui[2] / Ui[1]
        vti = Ui[3] / Ui[1]
        vui = Ui[4] / Ui[1]
        bni = Ui[6]
        bti = Ui[7]
        bui = Ui[8]
        # compute ro of intermediate states
        slvnl = sl - vnl
        srvnr = sr - vnr
        slsm = sl - sm
        srsm = sr - sm
        roil = rol * slvnl / slsm
        roir = ror * srvnr / srsm
        # compute ptot of left and right sides
        ptotl = prl + 0.5 * bl2
        ptotr = prr + 0.5 * br2
        # compute ptot of intermediate states
        ptoti = ptotl + rol * slvnl * (sm-vnl)
        # compute en of left intermediate states
        vibi = dot([sm, vti, vui], [bni, bti, bui])
        enil = (slvnl*Ul[5]-ptotl*vnl+ptoti*sm+bni*(vlbl-vibi)) / slsm
        # compute en of right intermediate states
        enir = (srvnr*Ur[5]-ptotr*vnr+ptoti*sm+bni*(vrbr-vibi)) / srsm
        # choose flux
        if sl > 0.0
            for m in 1:8
                F[m, i] = Fl[m]
            end
        elseif sl <= 0.0 < sm
            Uil = [roil, roil*sm, roil*vti, roil*vui, enil, bni, bti, bui]
            for m in 1:8
                F[m, i] = Fl[m] + sl * (Uil[m]-Ul[m])
            end
        elseif sm <= 0.0 < sr
            Uir = [roir, roir*sm, roir*vti, roir*vui, enir, bni, bti, bui]
            for m in 1:8
                F[m, i] = Fr[m] + sr * (Uir[m]-Ur[m])
            end
        elseif sr <= 0.0
            for m in 1:8
                F[m, i] = Fr[m]
            end                
        end
    end
end

あらかじめ保存量ベクトル\(\mathbf{U}\)や基本変数ベクトル\(\mathbf{V}\)から流束ベクトル\(\mathbf{F}\)を計算するconvert.jlなどを作成しておきます。 またconst.jlには比熱比\(\gamma\)などが定義されています。コード途中に出てくるUl, Vl, Flは左側の物理量における保存量、基本変数、流束ベクトルを表し、 Ur, Vr, Frは右側のものを意味します。

続いてHLLC-L流束計算コードのJulia実装例です。

using LinearAlgebra    
include("../convert/convert.jl")
include("../const/const.jl")
function hllcl!(F::Array{Float64, 2}, Vl::Array{Float64, 2}, Vr::Array{Float64, 2}, nxmax::Int64)
    for i in 1:nxmax-1
        rol = Vl[1, i]
        vnl = Vl[2, i]
        vtl = Vl[3, i]
        vul = Vl[4, i]
        prl = Vl[5, i]
        bnl = Vl[6, i]
        btl = Vl[7, i]
        bul = Vl[8, i]
        ror = Vr[1, i]
        vnr = Vr[2, i]
        vtr = Vr[3, i]
        vur = Vr[4, i]
        prr = Vr[5, i]
        bnr = Vr[6, i]
        btr = Vr[7, i]
        bur = Vr[8, i]
        # compute B * B of left side
        bl2 = dot(Vl[6:8, i], Vl[6:8, i])
        # compute v * B of left side
        vlbl = dot(Vl[2:4, i], Vl[6:8, i])
        # convert Vl ---> Ul
        Ul = Convert.v_to_u(Vl[:, i])
        # convert Ul, VL ---> Fl
        Fl = Convert.uv_to_f(Ul, Vl[:, i], bl2, vlbl)
        # compute B * B of right side
        br2 = dot(Vr[6:8, i], Vr[6:8, i])
        # compute v * B of right side
        vrbr = dot(Vr[2:4, i], Vr[6:8, i])
        # convert Vr ---> Ur
        Ur = Convert.v_to_u(Vr[:, i])
        # convert Ur, Vr ---> Fr
        Fr = Convert.uv_to_f(Ur, Vr[:, i], br2, vrbr)
        # compute fast-mode speed of left side
        gmprl = gm * prl
        vfl = sqrt(((bl2+gmprl)+sqrt((bl2+gmprl)^2-4*gmprl*bnl^2))/(2*rol))
        # compute fast-mode speed of right side
        gmprr = gm * prr
        vfr = sqrt(((br2+gmprr)+sqrt((br2+gmprr)^2-4*gmprr*bnr^2))/(2*ror))
        # compute sl, sr
        sl = min(vnl, vnr) - max(vfl, vfr)
        sr = max(vnl, vnr) + max(vfl, vfr)
        # compute HLL state U*
        Ui = (sr*Ur-sl*Ul-Fr+Fl) / (sr-sl)
        # compute sm(=vn), bn, bt, bu of intermediate states
        sm = Ui[2] / Ui[1]
        bni = Ui[6]
        bti = Ui[7]
        bui = Ui[8]
        # compute ro of intermediate states
        slvnl = sl - vnl
        srvnr = sr - vnr
        slsm = sl - sm
        srsm = sr - sm
        roil = rol * slvnl / slsm
        roir = ror * srvnr / srsm
        # compute vt, vu of intermediate states
        vtil = vtl + bni * (btl-bti) / (rol*slvnl)
        vtir = vtr + bni * (btr-bti) / (ror*srvnr)
        vuil = vul + bni * (bul-bui) / (rol*slvnl)
        vuir = vur + bni * (bur-bui) / (ror*srvnr)
        # compute ptot of left and right sides
        ptotl = prl + 0.5 * bl2
        ptotr = prr + 0.5 * br2
        # compute ptot of intermediate states
        ptoti = ptotl + rol * slvnl * (sm-vnl)
        # compute en of left intermediate states
        vilbil = dot([sm, vtil, vuil], [bni, bti, bui])
        enil = (slvnl*Ul[5]-ptotl*vnl+ptoti*sm+bni*(vlbl-vilbil)) / slsm
        # compute en of right intermediate states
        virbir = dot([sm, vtir, vuir], [bni, bti, bui])
        enir = (srvnr*Ur[5]-ptotr*vnr+ptoti*sm+bni*(vrbr-virbir)) / srsm
        # choose flux
        if sl > 0.0
            for m in 1:8
                F[m, i] = Fl[m]
            end
        elseif sl <= 0.0 < sm
            Uil = [roil, roil*sm, roil*vtil, roil*vuil, enil, bni, bti, bui]
            for m in 1:8
                F[m, i] = Fl[m] + sl * (Uil[m]-Ul[m])
            end
        elseif sm <= 0.0 < sr
            Uir = [roir, roir*sm, roir*vtir, roir*vuir, enir, bni, bti, bui]
            for m in 1:8
                F[m, i] = Fr[m] + sr * (Uir[m]-Ur[m])
            end
        elseif sr <= 0.0
            for m in 1:8
                F[m, i] = Fr[m]
            end                
        end
    end
end

以下にHLL, HLLC-G, HLLC-Lの3手法で、実際に磁気流体衝撃波管問題を解いて得られたガス密度分布を比較した図を示します。

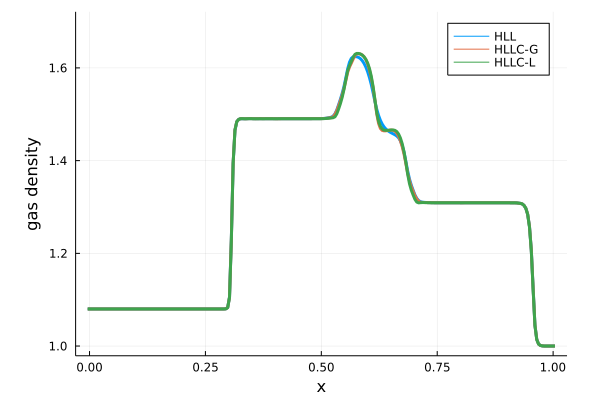
わかりにくいため、下に\(0.5 \leq x \leq 0.75\)の領域部分を拡大してプロットしたものを示します。

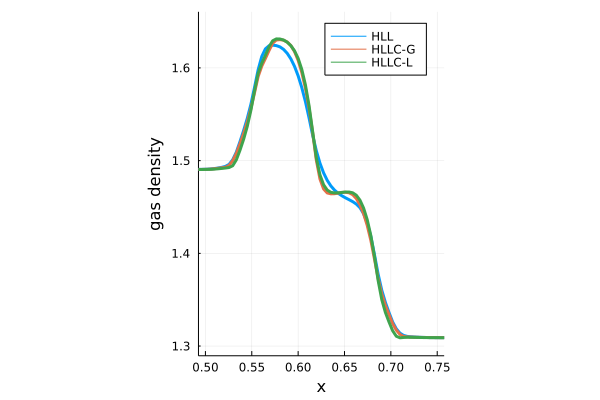
今回試した磁気流体衝撃波管問題では、HLLC-Lが一番構造をシャープに捉えられていることがわかります。

参考文献

• [1] Miyoshi & Kusano, 2005, “A multi-state HLL approximate Riemann solver for ideal magnetohydrodynamics”
• [2] Gurski, 2004, “An HLLC-type Approximate Riemann Solver for Ideal Magnetohydrodynamics”
• [3] Li, 2005, “An HLLC Riemann solver for magnetohydrodynamics”
• [4] Ryu & Jones, 1994, “Numerical Magnetohydrodynamics in Astrophysics: Algorithm and Tests for One-Dimensional Flow”
• [5] Stone et al., 2008, “Athena: A New Code for Astrophysical MHD”
• [6] Qiita記事, 磁気流体の数値計算で遊ぶ