Table of contents
磁気音波 (Magnetoacoustic waves, magnetosonic waves)
ここでは圧力を復元力として伝播する音波とアルヴェーン波がお互いに影響を及ぼし合った場合の波を考えます。
簡単な導出
音波の導出部分で出てきた分散関係式(20)において重力と回転を無視(\(g =0, \boldsymbol{\Omega}=\mathbf{0}\))し、さらに\(\mathbf{k} \cdot \hat{\mathbf{B}}_0 = k \cos \theta_B\)であることを用いて整理します。ここで\(\hat{\mathbf{B}}_0 = \mathbf{B}_0 / B_0\)です。
\[\begin{align} \frac{\omega^2}{v_A^2} \mathbf{v}_1 &= \frac{C_s^2}{v_A^2} (\mathbf{k} \cdot \mathbf{v}_1) \mathbf{k} + k^2 \cos^2 \theta_B \mathbf{v}_1 + \left\{ (\mathbf{k} \cdot \mathbf{v}_1) - k \cos \theta_B (\mathbf{v}_1 \cdot \hat{\mathbf{B}}_0)\right\} \mathbf{k} - (\mathbf{k} \cdot \mathbf{v}_1) k \cos \theta_B \hat{\mathbf{B}}_0 \notag \\ &= k^2 \cos^2 \theta_B \mathbf{v}_1 + \left\{ \left( 1+\frac{C_s^2}{v_A^2} \right)(\mathbf{k} \cdot \mathbf{v}_1) - k \cos \theta_B (\mathbf{v}_1 \cdot \hat{\mathbf{B}}_0)\right\} \mathbf{k} - k \cos \theta_B (\mathbf{k} \cdot \mathbf{v}_1) \hat{\mathbf{B}}_0 \tag{1} \end{align}\]まず、(1)式と\(\mathbf{k}\)との内積を取ります。
\[\begin{aligned} \frac{\omega^2}{v_A^2} \mathbf{v}_1 \cdot \mathbf{k} &= k^2 \cos^2 \theta_B \mathbf{v}_1 \cdot \mathbf{k} + \left\{ \left( 1 + \frac{C_s^2}{v_A^2} \right) (\mathbf{k} \cdot \mathbf{v}_1) - k \cos \theta_B (\mathbf{v}_1 \cdot \hat{\mathbf{B}}_0)\right\} k^2 - k \cos \theta_B (\mathbf{k} \cdot \mathbf{v}_1) (\mathbf{k} \cdot \hat{\mathbf{B}}_0) \\ &= \left\{ k^2 \cos^2 \theta_B + k^2 \left( 1+ \frac{C_s^2}{v_A^2} \right) -k^2 \cos^2 \theta_B \right\} (\mathbf{k} \cdot \mathbf{v}_1) - k^3 \cos \theta_B (\mathbf{v}_1 \cdot \hat{\mathbf{B}}_0) \\ &= k^2 \left( 1+\frac{C_s^2}{v_A^2} \right) \mathbf{k} \cdot \mathbf{v}_1 - k^3 \cos \theta_B (\mathbf{v}_1 \cdot \hat{\mathbf{B}}_0) \end{aligned}\]これを整理すると
\[\left\{ \frac{\omega^2}{v_A^2} - k^2 \left( 1+\frac{C_s^2}{v_A^2} \right) \right\} (\mathbf{k} \cdot \mathbf{v}_1) = k^3 \cos \theta_B \mathbf{v}_1 \cdot \hat{\mathbf{B}}_0 \tag{2}\]次に(1)式と\(\hat{\mathbf{B}}_0\)との内積を取ります。
\[\begin{align} \frac{\omega^2}{v_A^2} \mathbf{v}_1 \cdot \hat{\mathbf{B}}_0 &= k^2 \cos^2 \theta_B \mathbf{v}_1 \cdot \hat{\mathbf{B}}_0 + \left\{ \left( 1+\frac{C_s^2}{v_A^2} \right) (\mathbf{k} \cdot \mathbf{v}_1) - k \cos \theta_B (\mathbf{v}_1 \cdot \hat{\mathbf{B}}_0)\right\} \mathbf{k} \cdot \hat{\mathbf{B}}_0 - k \cos \theta_B (\mathbf{k} \cdot \mathbf{v}_1) \notag \\ &= \left( 1 + \frac{C_s^2}{v_A^2}\right) k\cos \theta_B \mathbf{k} \cdot \mathbf{v}_1 - k \cos \theta_B \mathbf{k} \cdot \mathbf{v}_1 = \frac{C_s^2}{v_A^2} k \cos \theta_B \mathbf{k} \cdot \mathbf{v}_1 \tag{3} \end{align}\](2), (3)式から、\(\mathbf{k} \cdot \mathbf{v}_1, \mathbf{v}_1 \cdot \hat{\mathbf{B}}_0\)を消去すると
\[\left\{ \frac{\omega^2}{v_A^2} - k^2 \left( 1 + \frac{C_s^2}{v_A^2} \right) \right\} \frac{v_A^2}{C_s^2 k \cos \theta_B} = k^3 \cos \theta_B \frac{v_A^2}{\omega^2} \ \Longrightarrow \ \frac{\omega^4}{k^4} - (v_A^2 + C_s^2) \frac{\omega^2}{k^2} - C_s^2 v_A^2 \cos^2 \theta_B = 0\]となります。この\(\omega^2 / k^2\)に関する2次方程式を解くと
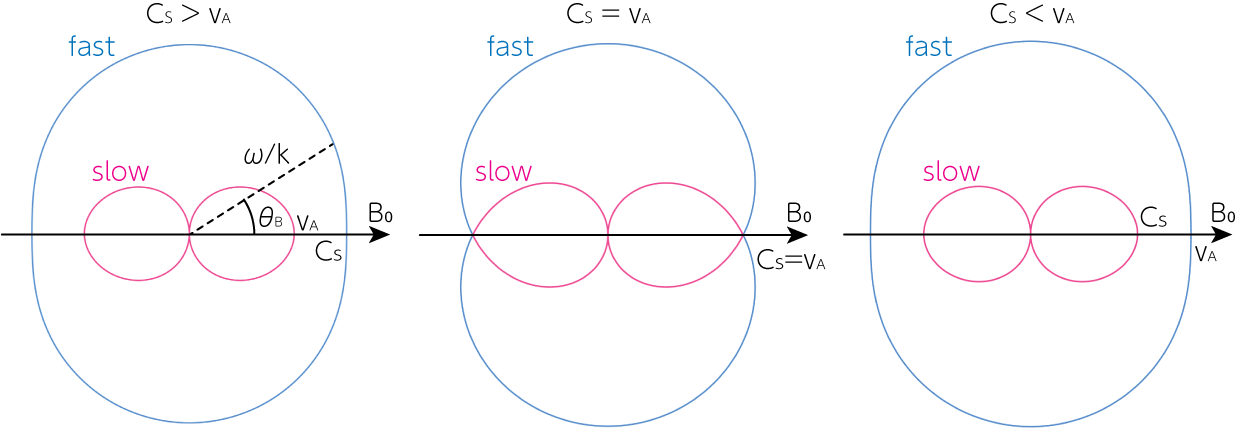
\[\frac{\omega^2}{k^2} = \frac{(v_A^2 + C_s^2) \pm \sqrt{(v_A^2 + C_s^2)^2 - 4 C_s^2 v_A^2 \cos^2 \theta_B}}{2} \tag{4}\]となり、分散関係式を得ます。\(+\)符号の位相速度の大きい波を速い磁気音波(fast-mode)、\(-\)符号の位相速度の小さい波を遅い磁気音波(slow-mode)と呼びます。速い磁気音波と遅い磁気音波における位相速度の背景磁場に対する角度依存性をフリードリックスダイアグラムにまとめると以下のようになります。音速\(C_s\)とアルヴェーン速度\(v_A\)の大きさによって振る舞いが変化します。
固有値・固有ベクトルを用いた解法
しかし、上述の議論だけでは実際にこの波動伝播中の流体がどのような振る舞いをしているのかを把握することができません。よって以下では固有値・固有ベクトルの方法を用いて、この分散関係式とその固有ベクトルを求めてみましょう。(1)式より
\[\omega^2 \mathbf{v}_1 = k^2 v_A^2 \cos^2 \theta_B \mathbf{v}_1 + \{ (v_A^2 + C_s^2) (\mathbf{k} \cdot \mathbf{v}_1) -k v_A^2 \cos \theta_B (\mathbf{v}_1 \cdot \hat{\mathbf{B}}_0)\} \mathbf{k} - kv_A^2 \cos \theta_B (\mathbf{k} \cdot \mathbf{v}_1) \hat{\mathbf{B}}_0\]今、背景磁場の方向として\(\hat{\mathbf{B}}_0\)は\(z\)方向を向いているとすると、\(\mathbf{k} \cdot \hat{\mathbf{B}}_0 = k \cos \theta_B\)より\(\mathbf{k} = (k \sin \theta_B, 0, k \cos \theta_B)\)のように書くことができます。規格化された波数ベクトルを\(\hat{\mathbf{k}} = \mathbf{k} / k\)、さらに\(\mathbf{v}_1 = (v_{1x}, v_{1y}, v_{1z})\)から
\[\begin{aligned} ( \omega^2 - k^2 v_A^2 \cos^2 \theta_B) \mathbf{v}_1 &= k \{ (v_A^2 + C_s^2) (v_{1x} \sin \theta_B + v_{1z} \cos \theta_B) - v_A^2 v_{1z} \cos \theta_B \} \mathbf{k} \\ & \qquad \qquad - k^2 v_A^2 \cos \theta_B (v_{1x} \sin \theta_B + v_{1z} \cos \theta_B) \hat{\mathbf{B}}_0 \\ &= k^2 \{ (v_A^2 + C_s^2) v_{1x} \sin \theta_B + C_s^2 v_{1z} \cos \theta_B\} \hat{\mathbf{k}} - k^2 v_A^2 \cos \theta_B (v_{1x} \sin \theta_B + v_{1z} \cos \theta_B) \hat{\mathbf{B}}_0 \end{aligned}\]以上からこれをベクトルの成分をあらわに書くと
\[\left( \begin{array}{c} (k^2 v_A^2 + k^2 C_s^2 \sin^2 \theta_B - \omega^2) v_{1x} + k^2 C_s^2 \sin \theta_B \cos \theta_B v_{1z} \\ (k^2 v_A^2 \cos^2 \theta_B - \omega^2) v_{1y} \\ k^2 C_s^2 \sin \theta_B \cos \theta_B v_{1x} + (k^2 C_s^2 \cos^2 \theta_B - \omega^2) v_{1z} \end{array} \right) = \mathbf{0}\]これを行列を用いて書けば
\[\left( \begin{array}{ccc} k^2 v_A^2 + k^2 C_s^2 \sin^2 \theta_B - \omega^2 & 0 & k^2 C_s^2 \sin \theta_B \cos \theta_B \\ 0 & k^2 v_A^2 \cos^2 \theta_B - \omega^2 & 0 \\ k^2 C_s^2 \sin \theta_B \cos \theta_B & 0 & k^2 C_s^2 \cos^2 \theta_B - \omega^2 \end{array} \right) \left( \begin{array}{c} v_{1x} \\ v_{1y} \\ v_{1z} \end{array}\right) = \mathbf{0} \tag{5}\]この行列の形から速度の摂動は\(\mathbf{k}, \mathbf{B}_0\)の両方に垂直な方向の変動\(v_{1y}\)の横波と、\(\mathbf{k}, \mathbf{B}_0\)の張る面内での変動\((v_{1x}, v_{1z})\)とに分けて考えることができます。
\(y\)方向
\(y\)方向の速度の摂動式は
\[(k^2 v_A^2 \cos^2 \theta_B-\omega^2) v_{1y} = 0 \ \Longrightarrow \ \omega = kv_A \cos \theta_B \tag{6}\]のように、シア・アルヴェーン波の分散関係式を得ます。
\(x, z\)方向
\(y\)方向とは独立に、\(x, z\)方向について
\[\left( \begin{array}{cc} k^2 v_A^2 + k^2 C_s^2 \sin^2 \theta_B - \omega^2 & k^2 C_s^2 \sin \theta_B \cos \theta_B \\ k^2 C_s^2 \sin \theta_B \cos \theta_B & k^2 C_s^2 \cos^2 \theta_B - \omega^2 \end{array} \right) \left( \begin{array}{c} v_{1x} \\ v_{1z} \end{array} \right) = \mathbf{0} \tag{7}\]任意の\((v_{1x}, v_{1z})\)で(7)式が成り立つためには、係数行列の行列式が0になれば良いでしょう。よって
\[\begin{aligned} &\left| \begin{array}{cc} k^2 v_A^2 + k^2 C_s^2 \sin^2 \theta_B - \omega^2 & k^2 C_s^2 \sin \theta_B \cos \theta_B \\ k^2 C_s^2 \sin \theta_B \cos \theta_B & k^2 C_s^2 \cos^2 \theta_B - \omega^2 \end{array} \right| \\ &= (\omega^2 - k^2 v_A^2 - k^2 C_s^2 \sin^2 \theta_B) (\omega^2 - k^2 C_s^2 \cos^2 \theta_B) - k^4 C_s^4 \sin^2 \theta_B \cos^2 \theta_B \\ &= \omega^4 - k^2 (v_A^2 + C_s^2) \omega^2 + k^4 v_A^2 C_s^2 \cos^2 \theta_B = 0 \end{aligned}\]となり、分散関係式
\[\omega^2 = \frac{1}{2} k^2 \left\{ v_A^2 + C_s^2 \pm \sqrt{(v_A^2 + C_s^2)^2 - 4 C_s^2 v_A^2 \cos^2 \theta_B}\right\} \tag{8}\]を得ます。これは(4)式と同じです。
このように分散関係式を得るのは簡単ですが、一般の磁場の大きさの場合においてこの波動中の流体の振る舞いを調べるのは簡単ではありません。よって以下ではある条件の下での(7)式の固有ベクトルを算出してみましょう。
\(C_s^2 \gg v_A^2\)(ガス圧優勢)のとき
\(\alpha \equiv v_A^2 / C_s^2\)とおくと、(8)式から
\[\begin{aligned} \omega^2 &= \frac{1}{2} k^2 C_s^2 \{ \alpha + 1 \pm \sqrt{(\alpha+1)^2 -4\alpha \cos^2 \theta_B} \} \underbrace{\simeq}_{\alpha^2 \sim 0} \frac{1}{2} k^2 C_s^2 \{ \alpha + 1 \pm \sqrt{1 + 2\alpha -4\alpha \cos^2 \theta_B} \} \\ &\underbrace{\simeq}_{テイラー展開} \frac{1}{2} k^2 C_s^2 [\alpha + 1 \pm \{ 1+ (1-2 \cos^2 \theta_B) \alpha \}] \end{aligned}\](i). 速い磁気音波
ここで\(\pm\)部分で\(+\)(速い磁気音波)を考えると
\[\omega_+^2 = k^2 C_s^2 (1+\alpha \sin^2 \theta_B)\]となります。ここから、(7)式の両辺を\(k^2 C_s^2\)で割ると
\[\begin{aligned} \left( \begin{array}{cc} \alpha + \sin^2 \theta_B - \frac{\omega^2}{k^2 C_s^2} & \sin \theta_B \cos \theta_B \\ \sin \theta_B \cos \theta_B & \cos^2 \theta_B - \frac{\omega^2}{k^2 C_s^2} \end{array} \right) \left(\begin{array}{c} v_{1x} \\ v_{1z} \end{array}\right) &= \left( \begin{array}{cc} \alpha + \sin^2 \theta_B - 1-\alpha \sin^2 \theta_B & \sin \theta_B \cos \theta_B \\ \sin \theta_B \cos \theta_B & \cos^2 \theta_B - 1-\alpha \sin^2 \theta_B \end{array} \right) \left(\begin{array}{c} v_{1x} \\ v_{1z} \end{array}\right) \\ &= \left( \begin{array}{cc} - (1-\alpha) \cos^2 \theta_B & \sin \theta_B \cos \theta_B \\ \sin \theta_B \cos \theta_B & - (1+\alpha) \sin^2 \theta_B \end{array} \right) \left(\begin{array}{c} v_{1x} \\ v_{1z} \end{array}\right) = \mathbf{0} \end{aligned}\]以上の連立方程式から
\[\frac{v_{1x}}{v_{1z}} = (1+\alpha) \tan \theta_B \ \Longrightarrow \ \mathbf{v}_1 = v_{1} ((1+\alpha)\sin \theta_B, \cos \theta_B)\]ここで\(v_{1} = \\|\mathbf{v}_1\\|\)としました。これより
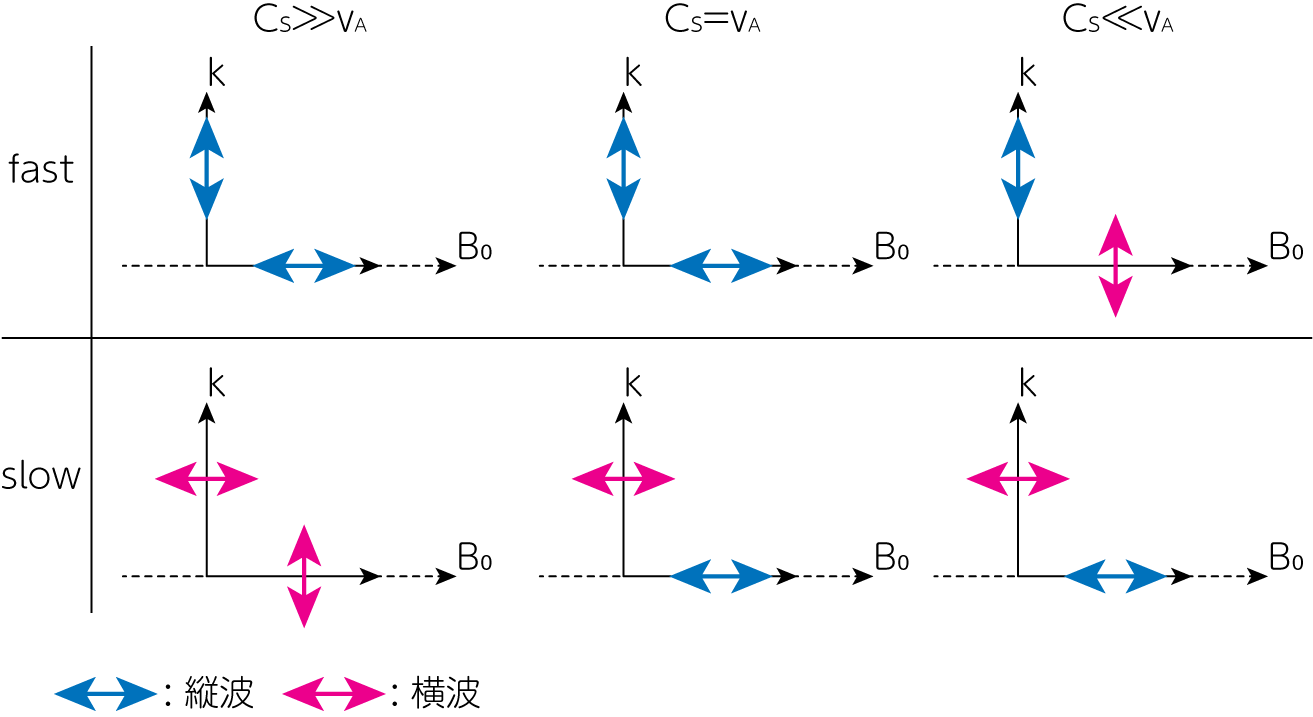
\[\mathbf{v}_1 \cdot \mathbf{k} = v_{1} k (1+\alpha \sin \theta_B) \tag{9}\]\(\alpha \ll 1\)から、(9)式は必ず正の値を取ります。波の進行方向を表す波数ベクトルと流体の速度ベクトルが同じ向きであることから、この場合の速い磁気音波は縦波的(音波的)であるとわかります。
(ii). 遅い磁気音波
同様に\(\pm\)で\(-\)(遅い磁気音波)を考えましょう。
\[\omega_-^2 = k^2 C_s^2 \alpha \cos^2 \theta_B\]です。よって
\[\begin{aligned} \left( \begin{array}{cc} \alpha + \sin^2 \theta_B - \frac{\omega^2}{k^2 C_s^2} & \sin \theta_B \cos \theta_B \\ \sin \theta_B \cos \theta_B & \cos^2 \theta_B - \frac{\omega^2}{k^2 C_s^2} \end{array} \right) \left(\begin{array}{c} v_{1x} \\ v_{1z} \end{array}\right) &= \left( \begin{array}{cc} \alpha + \sin^2 \theta_B - \alpha \cos^2 \theta_B & \sin \theta_B \cos \theta_B \\ \sin \theta_B \cos \theta_B & \cos^2 \theta_B - \alpha \cos^2 \theta_B \end{array} \right) \left(\begin{array}{c} v_{1x} \\ v_{1z} \end{array}\right) \\ &= \left( \begin{array}{cc} (1+\alpha) \sin^2 \theta_B & \sin \theta_B \cos \theta_B \\ \sin \theta_B \cos \theta_B & (1-\alpha) \cos^2 \theta_B \end{array} \right) \left(\begin{array}{c} v_{1x} \\ v_{1z} \end{array}\right) = \mathbf{0} \end{aligned}\]となります。以上の連立方程式から
\[\frac{v_{1x}}{v_{1z}} = - (1-\alpha) \cot \theta_B \ \Longrightarrow \ \mathbf{v}_1 = v_1 (-(1-\alpha) \cos \theta_B, \sin \theta_B)\]これより
\[\mathbf{v}_1 \cdot \mathbf{k} = v_1 k \alpha \sin \theta_B \cos \theta_B\]今、\(\alpha \ll 1\)よりこの値は十分に小さく、よって\(C_s^2 \gg v_A^2\)の極限では遅い磁気音波は横波的であることがわかります。
\(C_s = v_A\)(ガス圧と磁気圧が同程度)のとき
(8)式より
\[\omega^2 = \frac{1}{2} k^2 v_A^2 (2 \pm \sqrt{4-4\cos^2 \theta_B}) = k^2 v_A^2 (1 \pm \sin \theta_B)\](i). 速い磁気音波
速い磁気音波の場合は
\[\omega^2_+ = k^2 v_A^2 (1+\sin \theta_B)\]より、(7)式から
\[\left( \begin{array}{cc} \sin^2 \theta_B - \sin \theta_B & \sin \theta_B \cos \theta_B \\ \sin \theta_B & - \sin^2 \theta_B - \sin \theta_B \end{array} \right) \left( \begin{array}{c} v_{1x} \\ v_{1z} \end{array}\right) = \mathbf{0}\]となります。これより
\[\frac{v_{1x}}{v_{1z}} = \frac{\cos \theta_B}{1-\sin \theta_B} = \frac{1 + \sin \theta_B}{\cos \theta_B}\](ii). 遅い磁気音波
遅い磁気音波の場合は
\[\omega^2_- = k^2 v_A^2 (1-\sin \theta_B)\]より、(7)式から
\[\left( \begin{array}{cc} \sin^2 \theta_B + \sin \theta_B & \sin \theta_B \cos \theta_B \\ \sin \theta_B & - \sin^2 \theta_B + \sin \theta_B \end{array} \right) \left( \begin{array}{c} v_{1x} \\ v_{1z} \end{array}\right) = \mathbf{0}\]となります。これより
\[\frac{v_{1x}}{v_{1z}} = - \frac{\cos \theta_B}{1+\sin \theta_B} = - \frac{1 - \sin \theta_B}{\cos \theta_B}\]この場合はどの角度かによって\(v_{1x} / v_{1z}\)の値、すなわち\(\mathbf{k} \cdot \mathbf{v}_1\)の結果が変化します。よってこのままでは速い磁気音波・遅い磁気音波共に縦波か横波かを判断することが困難です。よって2つの極限でそれを考えてみましょう。
\(\theta_B \rightarrow 0\)のとき、すなわち\(z\)方向に波が進行するとき
\[\left\{ \begin{array}{l} 速い磁気音波: \mathbf{v}_{1f} = v_{1} (1, 1)\\ 遅い磁気音波: \mathbf{v}_{1s} = v_1 (-1, 1) \end{array} \right. \ \Longrightarrow \ \left\{ \begin{array}{l} \mathbf{k} \cdot \mathbf{v}_{1f} = v_1 k \\ \mathbf{k} \cdot \mathbf{v}_{1s} = v_1 k \end{array} \right.\]となり、どちらも縦波とわかります。次は\(\theta_B \rightarrow \pi/2\)のとき、すなわち\(x\)方向に波が進行するときについてです。
\[\left\{ \begin{array}{l} 速い磁気音波: \mathbf{v}_{1f} = v_1 (1, 0)\\ 遅い磁気音波: \mathbf{v}_{1s} = v_1 (0, 1) \end{array} \right. \ \Longrightarrow \ \left\{ \begin{array}{l} \mathbf{k} \cdot \mathbf{v}_{1f} = v_1 k \\ \mathbf{k} \cdot \mathbf{v}_{1s} = 0 \end{array} \right.\]となり、速い磁気音波は縦波、そして遅い磁気音波は横波です。
\(C_s^2 \ll v_A^2\)(磁気圧優勢)のとき
今度は\(\beta \equiv \frac{C_s^2}{v_A^2}\)のようにおくと、(8)式より
\[\begin{aligned} \frac{\omega^2}{k^2 v_A^2} &= \frac{1}{2} (1+\beta \pm \sqrt{(1+\beta)^2 - 4\beta \cos^2 \theta_B}) \underbrace{\simeq}_{\beta^2 \sim 0} \frac{1}{2} (1+\beta \pm \sqrt{1+ 2\beta (1-2 \cos^2 \theta_B)}) \\ &\underbrace{\simeq}_{テイラー展開} \frac{1}{2} [ 1+\beta \pm \{1+ (1-2\cos^2 \theta_B) \beta\} ] \end{aligned}\]さらに(7)式の両辺を\(k^2 v_A^2\)で割ったものから
\[\left( \begin{array}{cc} 1 + \beta \sin^2 \theta_B - \frac{\omega^2}{k^2 v_A^2} & \beta \sin \theta_B \cos \theta_B \\ \beta \sin \theta_B \cos \theta_B & \beta \cos^2 \theta_B - \frac{\omega^2}{k^2 v_A^2} \end{array}\right) \left( \begin{array}{c} v_{1x} \\ v_{1z} \end{array} \right) = \mathbf{0}\]磁気圧が優勢の場合の固有ベクトルを求めることは至難の技です。というのも、理想磁気流体においては磁束凍結定理から、流体要素の運動は磁場に沿った方向に大きく制限されます。このため、流体の速度が波の進行方向に関係するかどうかは定かではありません。よってここでは固有ベクトルを求めずに
\[\left( 1+\beta \sin^2 \theta_B - \frac{\omega^2}{k^2 v_A^2}\right) v_{1x} + \alpha \sin \theta_B \cos \theta_B v_{1z} = 0 \ \Longrightarrow \ \frac{v_{1x}}{v_{1z}} = \frac{\beta \sin \theta_B \cos \theta_B}{\frac{\omega^2}{k^2 v_A^2} - 1 - \beta \sin^2 \theta_B}\]から波動の様子を見てみましょう。
(i). 速い磁気音波
\[\frac{\omega_+^2}{k^2 v_A^2} = 1 + \beta \sin^2 \theta_B\]の場合、\(v_{1x} / v_{1z} \rightarrow \infty\)となります。すなわち\(v_{1x} = v_1, v_{1z} = 0\)となります。これは\(z\)方向磁場に対して垂直な方向にのみ流体が動くことを示しています。このことから\(\theta_B = 0\)では横波、\(\theta_B= \pi/2\)では縦波となることを意味します。
(ii). 遅い磁気音波
\[\frac{\omega_-^2}{k^2 v_A^2} = \beta \cos^2 \theta_B\]の場合
\[\frac{v_{1x}}{v_{1z}} = \frac{\beta \sin \theta_B \cos \theta_B}{\beta \cos^2 \theta_B - 1 - \beta \sin^2 \theta_B} \ll 1\]となります。すなわち\(v_{1x} = 0, v_{1z} = v_1\)となります。これは\(z\)方向に磁場に対して平行な方向にのみ流体が動くことを示しています。このことから\(\theta_B = 0\)では縦波、\(\theta_B = \pi/2\)では横波となることを意味します。
長くなりましたが、磁場が弱いときと強いとき、さらには伝播方向の違いで、同一のモードであるにもかかわらず縦波(音波的振動)と横波(アルヴェーン的振動)との入れ替わりが起こることがわかります。これまでの議論をまとめると以下の図に集約されます。
\(C_s \gg v_A\)の場合の物理的解釈
速い磁気音波
この状況では速い磁気音波は音波によって駆動されていると考えることができます。このとき、磁場に沿った方向は音波そのままです。しかし、磁場に垂直な方向への波動は、音波の振動から磁場も同じように振動をします。すると下図のように磁力線が密の部分が形成されます。これにより生じる磁気圧勾配力と、音波による圧縮で生じるガス圧勾配力が協力することで、大きな復元力が生まれます。これが速い磁気音波の位相速度が磁場に垂直な方向に大きくなる理由です。
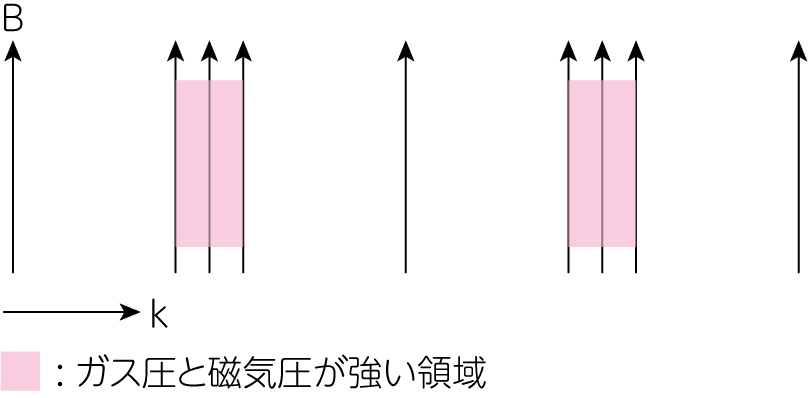
遅い磁気音波
この状況では遅い磁気音波は横波のアルヴェーン波によって駆動されていると考えることができます。このとき、磁場に沿った方向はアルヴェーン波そのままです。しかし、磁場に垂直な方向へは、磁気張力による(ゴム紐のような)振動は伝播することができません。これが遅い磁気音波の位相速度が磁場に垂直な方向ではゼロになる理由です。
\(C_s \ll v_A\)の場合の物理的解釈
速い磁気音波
この状況では速い磁気音波はアルヴェーン波によって駆動されていると考えることができます。このとき、磁場に沿った方向は磁気張力を復元力とする横波のアルヴェーン波、そして磁場に垂直な方向へは磁気圧勾配力を復元力とするアルヴェーン波が伝播します。しかし先程と同様に、磁力線が密の部分が作られると同時にガスも圧縮を受けます。磁気圧勾配力で伝播するアルヴェーン波と、それによって生じるガス圧縮によるガス圧勾配力の協力が起きることで、速い磁気音波として波動が伝播します。
遅い磁気音波
この状況では遅い磁気音波は音波によって駆動されていると考えることができます。このとき、磁場に沿った方向は音波そのままです。しかし、磁場に垂直な方向への音波の伝播を考えると、今は磁場が強力な場合を考えているため、(まるで磁場の檻に閉じ込められているかのように)流体要素は磁場を横切る方向に振動をすることができません。よってこの場合も遅い磁気音波は、磁場に垂直な方向に伝播することができず、位相速度がゼロとなることがわかります。
遅い磁気音波の磁場に沿った方向の位相速度の\(\theta_B \rightarrow \pi/2\)極限
再び(8)式に戻りましょう。ここから遅い磁気音波に対して、その位相速度の磁場に沿った成分を考えると
\[\frac{\omega^2_-}{k^2 \cos^2 \theta_B} = \frac{C_s^2 + v_A^2 - \sqrt{(C_s^2 + v_A^2)^2 - 4 C_s^2 v_A^2 \cos^2 \theta_B}}{2 \cos^2 \theta_B}\]これの\(\theta_B \rightarrow \pi/2\)極限を考えましょう。これまでの議論から考えると\(\theta_B = \pi/2\)の方向へは遅い磁気音波は伝播しないことになっています。しかし、以下のように厳密に計算すると、磁場に沿った成分が極限として残ります。ロピタルの定理より
\[\begin{aligned} \lim_{\theta_B \rightarrow \pi/2} \frac{\omega^2_-}{k^2 \cos^2 \theta_B} &= \lim_{\theta_B \rightarrow \pi/2} \frac{- \frac{8C_s^2 v_A^2 \sin \theta_B \cos \theta_B}{\sqrt{(C_s^2+ v_A^2)^2 -4C_s^2 v_A^2 \cos^2 \theta_B}}}{-4 \sin \theta_B \cos \theta_B} = \lim_{\theta_B \rightarrow \pi/2} \frac{C_s^2 v_A^2 \sin 2\theta_B}{\sin 2\theta_B \sqrt{(C_s^2+ v_A^2)^2 -4C_s^2 v_A^2 \cos^2 \theta_B}} \\ &= \frac{C_s^2 v_A^2}{C_s^2 + v_A^2} \end{aligned}\]のようになります。これは破面がつまっていくことにより、それを射影した成分が0ではなく有限の値となることを意味しています。
群速度
最後に群速度を計算しましょう。その定義から
\[\mathbf{v}_g = \frac{\partial \omega}{\partial \mathbf{k}} = \frac{\partial \omega}{\partial k} \mathbf{e}_k + \frac{1}{k} \frac{\partial \omega}{\partial \theta_B} \mathbf{e}_{\theta_B}\](8)式より\(\omega \propto k\)から、第1項はそのまま位相速度\(v_p\)になります。第2項の計算は以下のようにして行います。
\[\frac{1}{k^2} \frac{\partial \omega^2}{\partial \theta_B} = \frac{2 \omega}{k^2} \frac{\partial \omega}{\partial \theta_B} = \pm \frac{1}{4} \frac{8 C_s^2 v_A^2 \cos \theta_B \sin \theta_B}{\sqrt{(C_s^2 + v_A^2)^2 - 4 C_s^2 v_A^2 \cos^2 \theta_B}}\]ここから
\[\frac{1}{k} \frac{\partial \omega}{\partial \theta_B} = \frac{k}{\omega} \frac{\pm C_s^2 v_A^2 \cos \theta_B \sin \theta_B}{\sqrt{(C_s^2 + v_A^2)^2 - 4 C_s^2 v_A^2 \cos^2 \theta_B}} = \pm \frac{k \cos \theta_B}{\omega} \frac{C_s^2 v_A^2 \sin \theta_B}{\sqrt{(C_s^2 + v_A^2)^2 - 4 C_s^2 v_A^2 \cos^2 \theta_B}}\]以上より
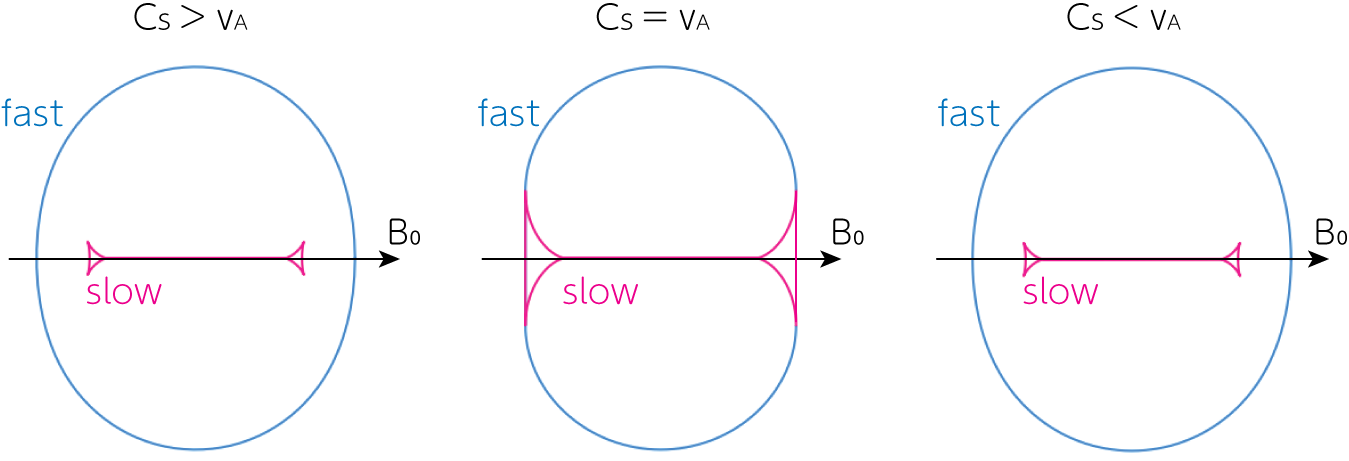
\[\mathbf{v}_g = v_p \mathbf{e}_k \pm \frac{k \cos \theta_B}{\omega} \frac{C_s^2 v_A^2 \sin \theta_B}{\sqrt{(C_s^2 + v_A^2)^2 - 4 C_s^2 v_A^2 \cos^2 \theta_B}} \mathbf{e}_{\theta_B} \tag{10}\]です。速い磁気音波では\(k/\omega = v_p^{-1}\)はどの\(\theta_B\)方向においても有限の値を持ちます。しかし遅い磁気音波では\(\theta_B \rightarrow \pi/2\)の極限で\(v_p \rightarrow 0, \frac{k \cos \theta_B}{\omega} \rightarrow \frac{\sqrt{C_s^2 + v_A^2}}{C_s v_A}\)のようになるため、特別な値となります。最終的に
\[c_T = \frac{C_s v_A}{\sqrt{C_s^2+ v_A^2}} \tag{11}\]のようになり、これをカスプ速度(cusp speed)と呼びます。
群速度を図示したものを以下に示します。
参考文献
[1] Priest, “Solar Magnetohydrodynamics”
[2] 観山正見, 野本憲一, 二間瀬敏史, “天体物理学の基礎 II”
[3] 加藤正二, “天体物理学基礎理論”