過冷却状態の熱力学的な議論
以下の問題は、2023年に行われた北海道大学大学院理学院宇宙理学専攻の大学院入試問題です。 最初はエンタルピーなどの基本的な問題ののち、それを用いて過冷却状態にある液体から固体への変化について議論しています。 過冷却状態はあまり馴染みがないかもしれませんが、基本を理解できていれば解けるはずです。 落ち着いて解き進めていきましょう。
問題
問1
系の内部エネルギーを\(U\)、エンタルピーを\(H\)、エントロピーを\(S\)、絶対温度を\(T\)、圧力を\(p\)、体積を\(V\)として以下の問いに答えなさい。
1-1
熱力学第一法則より、系に\(d'Q\)の熱量を準静的に与えた場合、以下の式が成り立ちます。
\[d'Q = dU + pdV \tag{1}\]\(H = U + pV\)と表されることを用いて、以下の式が成り立つことを示しなさい。
\[d'Q = dH - V dp \tag{2}\]1-2
エンタルピーを\(H(T, p)\)のように温度と圧力の関数と考えると、\(d'Q\)が以下の式で表されることを示しなさい。
\[d'Q = \left( \frac{\partial H}{\partial T}\right)_p dT + \left\{ \left(\frac{\partial H}{\partial p}\right)_T - V\right\} dp \tag{3}\]1-3
定圧条件下で\(d'Q\)の熱量を系に準静的に与えるとき、系の温度が\(dT\)上昇した場合、系の定圧熱容量は\(C_p = \left( \frac{d'Q}{dT}\right)_p\)と表されます。 1-2の結果と\(dS = \frac{d'Q}{T}\)の関係を用いて、以下の関係式を示しなさい。
\[\left( \frac{\partial H}{\partial T}\right)_p = C_p, \quad \left( \frac{\partial S}{\partial T}\right)_p = \frac{C_p}{T} \tag{3}\]問2
問1の結果を用いて、以下の問題に答えなさい。
過冷却状態とは、物質が凝固点(融点)以下まで液体状態を保った準安定な状態です。 ここでは以下の過程のもとで、過冷却状態を示すある物質Xが凝固点以下の温度で過冷却液体から固体に状態変化する過程でのエントロピー変化について、図1を参考にしながら考えてみましょう。
物質Xの1気圧での固体状態での定圧モル比熱を\(C_s\)、液体状態の定圧モル比熱を\(C_l\)とします。 \(C_s, C_l\)は温度に依存せずに一定で、\(C_s < C_l\)とします。 また、過冷却状態での液体の定圧モル比熱も\(C_l\)であり、平衡状態での液体と同様に扱うことができるものとします。 物質Xの1気圧での融点は\(T_0\)であり、1気圧かつ温度\(T_0\)でのモル融解熱を\(Q_0\)とします。 過冷却液体から固体に変化する温度を\(T_1 (< T_0)\)とし、\(T > T_1\)の範囲では、液体状態のエントロピーは固体状態のエントロピーより大きいものとします。 全て1モルの物質Xの1気圧での定圧変化を考えるものとして、以下の問題に\(C_s, C_l, T_0, T_1, Q_0\)を用いて答えてみましょう。
2-1
物質Xを温度\(T_1\)の固体から温度\(T_0\)の液体に変化(図1のA->B->Cの変化)させるのに必要となる熱量\(Q_1\)と物質Xのエントロピー変化\(\Delta S_1\)を求めなさい。
同様に、温度\(T_0\)の液体から温度\(T_1\)の過冷却液体に変化(図1のC->Dの変化)させるのに必要となる熱量\(Q_2\)と物質Xのエントロピー変化\(\Delta S_2\)を求めなさい。
2-2
物質Xが温度\(T_1\)の過冷却液体から同じ温度\(T_1\)の固体に変化する過程は、図1でD->Aの変化に対応します。 この過程が不可逆過程であることに注意して、物質Xが温度\(T_1\)の過冷却液体から温度\(T_1\)の固体に変化する過程での物質Xのエントロピー変化\(\Delta S_3\)を求めなさい。
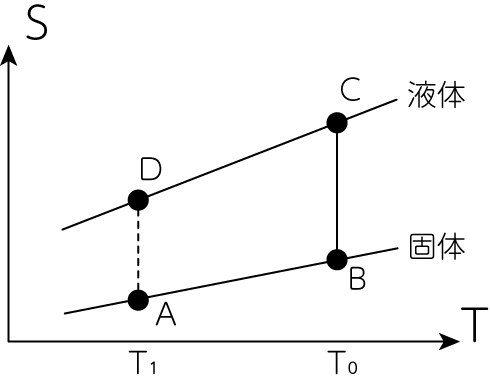
図1: 物質Xの温度-エントロピー図
解答例
問1
1-1
\[H = U + pV \ \Longrightarrow \ dH = dU + pdV + Vdp \tag{1-1-1}\]より
\[d'Q = dU + dH - dU - Vdp = dH - Vdp \tag{1-1-2}\]1-2
\(H(T, p)\)より
\[dH = \left( \frac{\partial H}{\partial T}\right)_p dT + \left( \frac{\partial H}{\partial p}\right)_T dp \tag{1-2-1}\]と書けます。 この式と(1-1-2)より
\[d'Q = \left( \frac{\partial H}{\partial T}\right)_p dT + \left\{ \left( \frac{\partial H}{\partial p}\right)_T - V\right\}dp \tag{1-2-2}\]1-3
(1-2-2)式より
\[C_p = \left( \frac{d'Q}{dT}\right)_p = \left( \frac{\partial H}{\partial T}\right)_p \tag{1-3-1}\]また\(dS = \frac{d'Q}{T}\)より
\[\left( \frac{\partial S}{\partial T}\right)_p = \frac{1}{T} \left( \frac{d'Q}{dT}\right)_p \underbrace{=}_{(1-3-1)} \frac{C_p}{T} \tag{1-3-2}\]問2
2-1
A->Bの変化で必要な熱量とエントロピー変化をそれぞれ\(Q_\mathrm{AB}, \Delta S_\mathrm{AB}\)とすると
\[Q_\mathrm{AB} = C_s (T_0 - T_1) \tag{2-1-1}\] \[\Delta S_\mathrm{AB} = \int_{T_1}^{T_0} \frac{C_s}{T} dT = C_s \ln \frac{T_0}{T_1} \tag{2-1-2}\]です。 そしてB->Cの変化で必要な熱量とエントロピー変化をそれぞれ\(Q_\mathrm{BC}, \Delta S_\mathrm{BC}\)とすると
\[Q_\mathrm{BC} = Q_0 \tag{2-1-3}\] \[\Delta S_\mathrm{BC} = \frac{Q_0}{T_0} \tag{2-1-4}\]のように求まります。 以上より
\[Q_1 = Q_\mathrm{AB} + Q_\mathrm{BC} = C_s (T_0 - T_1) + Q_0 \tag{2-1-5}\] \[\Delta S_1 = \Delta S_\mathrm{AB} + \Delta S_\mathrm{BC} = C_s \ln \frac{T_0}{T_1} + \frac{Q_0}{T_0} \tag{2-1-6}\]C->Dの変化で必要な熱量\(Q_2\)は
\[Q_2 = C_l (T_1 - T_0) \tag{2-1-7}\]そしてエントロピー変化\(\Delta S_2\)は
\[\Delta S_2 = \int_{T_0}^{T_1} \frac{C_l}{T} dT = C_l \ln \frac{T_1}{T_0} \tag{2-1-8}\]と求まります。 液体を冷やすC->Dの過程は、\(Q_2 < 0, \Delta S_2 < 0\)となっていることがわかります。
2-2
D->Aの過程でのエントロピー変化\(\Delta S_3\)は、D->C->B->Aの変化で起こるエントロピー変化と同じと考えることができるので
\[\Delta S_3 = - \Delta S_2 - \Delta S_1 = -C_l \ln \frac{T_1}{T_0} - C_s \ln \frac{T_0}{T_1} - \frac{Q_0}{T_0} = (C_l - C_s) \ln \frac{T_0}{T_1} - \frac{Q_0}{T_0} \tag{2-2-1}\]のように計算されます。 題意からは逸れますが、D->Aで外界が得る熱量を計算してみましょう。
\[Q_\mathrm{out} = - Q_1 - Q_2 = -C_s (T_0 - T_1) - Q_0 - C_l (T_1 - T_0) = (C_l - C_s) (T_0 - T_1) - Q_0 \tag{2-2-2}\]外界は熱容量が無限大であり、温度変化はせずに常に一定の温度\(T_1\)であったとすると
\[\Delta S_\mathrm{out} = \frac{Q_\mathrm{out}}{T_1} = (C_l - C_s) \frac{T_0 - T_1}{T_1} - \frac{Q_0}{T_1} \tag{2-2-3}\]のようになります。 以上から、外界とのやりとりも含めたエントロピーの変化は
\[\Delta S + \Delta S_\mathrm{out} = (C_l - C_s) \left( \ln \frac{T_0}{T_1} + \frac{T_0 - T_1}{T_1} \right) - Q_0 \left( \frac{1}{T_0} + \frac{1}{T_1}\right) \neq 0 \tag{2-2-4}\]のように、ゼロではない値となります。 このことからも、過冷却状態の液体が固体に変化する過程が不可逆過程であることがわかります。
本当はこれが常に正であることを言いたいのだけれど、おそらくそれはCl, Cs, T0, T1, Q0の値に依存するので難しい?
参考文献
[1] 北海道大学大学院理学院(宇宙理学専攻)、令和6年度修士課程入学試験
[2] home-01.com, “過冷却とエンタルピー変化・エントロピー変化”