3.4 Local Thermodynamic Equilibrium (LTE)

多くの場合、ガス粒子の平均自由行程は恒星大気内で温度・圧力などの物理量が変化する距離に比べて非常に小さいです。よってガスの状態はそれぞれの場所の温度・密度に対する熱平衡状態(LTE)になっている場合が多いです。LTEの場合、ガス粒子の性質が場所場所の温度・密度だけで決まるため、取り扱いが簡単になります。

3.4.1 Maxwell分布

十分に希薄で熱平衡なガスの運動はMaxwell分布

\[f(v) dv = \left( \frac{m}{2\pi k_B T} \right)^{3/2} e^{-\frac{mv^2}{2k_B T}} 4\pi v^2 dv \tag{3.42}\]

で与えられます。このとき、速度の2乗の平均の平方根(Root-mean-square velocity)は\(\sqrt{\langle v^2 \rangle} = \sqrt{\frac{3k_B T}{m}}\)です。

3.4.2 Boltzmannの励起法則

熱平衡状態では、原子またはイオンの各エネルギー準位状態にある確率はBoltzmannの法則で与えられます。ある原子(またはイオン)\(i\)に対して、基底状態にある\(n_{i, 0}\)と、ある励起状態\(k\)にある数\(n_{i, k}\)との比は

\[\left( \frac{n_{i, k}}{n_{i, 0}}\right)^\ast = \frac{g_{i, k}}{g_{i, 0}} e^{-\frac{\chi_{i, k}}{k_B T}} \tag{3.43}\]

のように与えられます。ここで\(\chi_{i, k}\)は状態\(k\)の励起エネルギーを表し、\(g_{i, 0}, g_{i, k}\)はそれぞれ基底状態と励起状態\(k\)の統計的重率(Statistical weight)を表します。さらに\(\ast\)は熱平衡状態の値であることを表します。
\(N_i\)を原子\(i\)の数密度とすると、熱平衡状態では

\[\begin{align} N_i &= \sum_{k=0}^\infty n_{i, k} = n_{i, 0}^\ast \sum_{k=0}^\infty \left( \frac{n_{i, k}}{n_{i, 0}}\right)^\ast \underbrace{=}_{(3.43)} n_{i, 0}^\ast \sum_{k=0}^\infty \frac{g_{i, k}}{g_{i, 0}} e^{-\frac{\chi_{i, k}}{k_B T}} = \frac{n_{i, 0}^\ast}{g_{i, 0}} \left( g_{i, 0} + \sum_{k=1}^\infty g_{i, k} e^{-\frac{\chi_{i, k}}{k_B T}}\right) \notag \\ &= \frac{n_{i, 0}^\ast}{g_{i, 0}} U_i (T) \tag{3.44} \end{align}\]

のように書けます。ここで\(U_i(T)\)は

\[U_i (T) \equiv \sum_{k=0}^\infty g_{i, k} e^{-\frac{\chi_{i, k}}{k_B T}} \tag{3.45}\]

のように定義される分配関数(Partition function)です。ちなみに、この式では\(\chi_{i, 0}= 0\)です。この式は分配関数が各エネルギー状態の統計的重率を、そのエネルギー準位の実現確率をWeightにして加えたものであることを示しています。したがって、分配関数はある与えられた温度に対して、原子の状態の平均的自由度を表していると言えます。
今後のために、以下のように式変形を行いましょう。

\[\frac{n_{i, k}^\ast}{N_i} = \left( \frac{n_{i, k}}{n_{i, 0}}\right)^\ast \frac{n_{i, 0}^\ast}{N_i} \underbrace{=}_{(3.43), (3.44)} \frac{g_{i, k}}{g_{i, 0}} e^{-\frac{\chi_{i, k}}{k_B T}} \frac{n_{i, 0}^\ast g_{i, 0}}{n_{i, 0}^\ast U_i (T)} = \frac{g_{i, k}}{U_i (T)} e^{-\frac{\chi_{i, k}}{k_B T}} \tag{3.46}\]

3.4.3 Sahaの電離式

電離したものとしていないものとの数の比を得るために、Boltzmannの法則を使います。原子\(i\)が1回電離してイオン\(i+1\)ができたとして、その数を\(N_{i+1}\)とします。(3.44)と同様に

\[N_{i+1} = \frac{n_{i+1, 0}^\ast}{g_{i+1, 0}} U_{i+1} (T) \tag{3.47}\]

が成り立つので

\[\frac{N_{i+1}}{N_i} = \frac{g_{i, 0}}{g_{i+1, 0}} \frac{U_{i+1}}{U_i} \left( \frac{n_{i+1, 0}}{n_{i, 0}}\right)^\ast \tag{3.48}\]

と書くことができます。この式に現れる\(\left( \frac{n_{i+1, 0}}{n_{i, 0}}\right)^\ast\)にBoltzmannの法則を適用します。これら2つの状態のエネルギー差は電離エネルギーで、それを\(\chi_I\)と書きましょう。電離した状態の統計的重率は、イオン自体の統計的重率\(g_{i+1, 0}\)と自由電子の分配関数\(U_e\)を掛け合わせたもの、すなわち\(g_{i+1, 0} U_e\)となります。したがって

\[\left( \frac{n_{i+1, 0}}{n_{i, 0}}\right)^\ast = \frac{g_{i+1, 0} U_e}{g_{i, 0}} e^{-\frac{\chi_I}{k_B T}} \tag{3.49}\]

のように表されます。これを(3.48)式に代入すると

\[\frac{N_{i+1}}{N_i} = \frac{U_e U_{i+1}}{U_i} e^{-\frac{\chi_I}{k_B T}} \tag{3.50}\]

を得ます。よってあとは\(U_e\)がわかれば良いことがわかります。
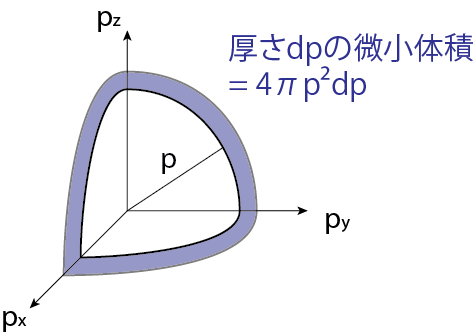
自由電子の分配関数\(U_e\)を以下のようにして求めていきましょう。まずは、運動量が\((p, p+dp)\)の範囲にある自由電子の単位堆積あたりの状態数(統計的重率)を求めます。電子数密度\(n_e\)より、電子1個あたりが占有する空間体積は\(\Delta x^3 = 1/n_e\)です。運動量空間において半径\(p\), 厚さ\(dp\)の球殻の体積は\(4\pi p^2 dp\)です。

運動量空間での球殻の体積。

不確定性原理から、1つの電子が占有する体積は\(h^3\)です。これらを総合して、知りたかった状態数は

\[\frac{4\pi p^2 dp}{n_e h^3} \times 2\]

となります。最後の2は電子のスピン自由度です。今は自由電子について考えているので、実現確率の重みを\(e^{-\frac{E}{k_B T}} = e^{-\frac{p^2}{2m k_B T}}\)のように連続状態に適用して

\[U_e = \int_0^\infty \frac{8\pi p^2}{n_e h^3} e^{-\frac{p^2}{2mk_B T}} dp = \frac{8\pi}{h^3 n_e} \frac{1}{4} (2mk_B T)^{3/2} \sqrt{\pi} = \frac{2}{n_e} \left( \frac{2\pi m k_B T}{h^2}\right)^{3/2} \tag{3.51}\]

を得ます。これを(3.50)式に代入すると

\[\frac{N_{i+1} n_e}{N_i} = 2 \left( \frac{2\pi m_e k_B T}{h^2}\right)^{3/2} \frac{U_{i+1}}{U_i} e^{-\frac{\chi_I}{k_B T}} \tag{3.52}\]

が得られます。この式がSahaの電離式の1つの形です。
電子は原子またはイオンから放出されるため、電子数密度は質量密度\(\rho\)に比例します。すなわち\(n_e \propto \rho\)です。(3.52)式を変形すると

\[\frac{N_{i+1}}{N_i} \propto \frac{e^{-\frac{\chi_I}{k_B T}}}{\rho}\]

となります。このことから、ガス密度\(\rho\)が大きいと\(N_{i+1}/N_i\)が小さくなることがわかります。これは電子の数が多くなることで、再結合する確率も高くなり、電離度が下がるためです。