Table of contents
カー・ブラックホールの特徴
質量\(M\)、自転角運動量\(J\)のカー・ブラックホールの線素は以下のように書けるのでした。
\[ds^2 = - \frac{\Delta -a^2 \sin^2 \theta}{\rho^2} c^2 dt^2 - \frac{2 a r_g r \sin^2 \theta}{\rho^2} c dt d\varphi + \frac{(r^2 + a^2)^2 -a^2 \Delta \sin^2 \theta}{\rho^2} \sin^2 \theta d\varphi^2 + \frac{\rho^2}{\Delta} dr^2 + \rho^2 d\theta^2 \tag{1}\]ここで\(\Delta = r^2 - r_g r + a^2, r_g = 2GM/c^2, a = J / (Mc), \rho^2 = r^2 + a^2\cos^2 \theta\)です。
以下では記述をスッキリさせるために
\[g_{00} = - \frac{\Delta -a^2 \sin^2 \theta}{\rho^2}, \quad g_{0\varphi} = - \frac{a r_g r \sin^2 \theta}{\rho^2}, \quad g_{\varphi \varphi} = \frac{(r^2 + a^2)^2 -a^2 \Delta \sin^2 \theta}{\rho^2} \sin^2 \theta\]のように表記します。
エルゴ領域
\(z = r \cos \theta\)が一定かつ\(r\)一定の縁に接する方向に放たれた光の軌跡を考えましょう。今の問題設定と、光がnull pathを通ることから
\[0 = g_{00} c^2 dt^2 + 2 g_{0\varphi} c dt d \varphi + g_{\varphi \varphi} d\varphi^2 \tag{2}\]これの両辺を\(dt^2\)で割ると
\[g_{\varphi \varphi} \left(\frac{d\varphi}{dt} \right)^2 + 2 g_{0\varphi} c \frac{d\varphi}{dt} + c^2 g_{00} = 0\]のように、光の\(\varphi\)方向の時間変化、つまり角速度の式になります。2次方程式の解の公式より
\[\frac{d\varphi}{dt} = - \frac{g_{0\varphi}}{g_{\varphi \varphi}} \pm c \sqrt{\left( \frac{g_{0\varphi}}{g_{\varphi \varphi}}\right)^2 - \frac{g_{00}}{g_{\varphi \varphi}}} \tag{3}\]のようになります。特に、\(g_{00}=0\)となる面では、角速度は
\[\frac{d\varphi}{dt} = \left\{ \begin{array} - c \frac{2 g_{0\varphi}}{g_{\varphi \varphi}} = 2c \frac{a r_g r }{(r^2+a^2)^2 - a^2 \Delta \sin^2 \theta }\\ 0 \end{array} \right. \tag{4}\]の2つの解を持つことがわかります。最初の解はブラックホールの自転角運動量\(J\)と同じ方向に引きずられることを表しています。もう一つの0となる解はブラックホールの回転と逆方向に放出された光子が全く動かない解を表しています。光子よりも速く移動することができる粒子は存在しないため、この境界面では全ての粒子がブラックホールと同じ方向に回転せざるを得ないことがわかります。この境界面をエルゴ球 (ergosphere)と呼びます。エルゴ球の半径は、先程の議論から\(g_{00} = 0\)より求まります。
\[g_{00} = - \frac{\Delta - a^2 \sin^2 \theta}{\rho^2} = r^2 - r_g r + a^2 \cos^2 \theta = 0 \ \Longrightarrow \ r_\mathrm{ergo} = \frac{r_g \pm \sqrt{r_g^2 - 4 a^2 \cos^2 \theta}}{2} \tag{5}\]地平面
シュバルツシルト時空において\(r=r_g\)、すなわち\(g_{rr} = \infty\)となる場所が事象の地平面でした。このアナロジーを用いると、カー・ブラックホールにおける事象の地平面は
\[g_{rr} = \frac{\rho^2}{\Delta} = \infty \ \Longrightarrow \ \Delta = r^2 - r_g r + a^2 = 0 \ \Longrightarrow \ r_+ = \frac{r_g + \sqrt{r_g^2 - 4a^2}}{2} \tag{6}\](5), (6)式を比較すると、事象の地平面はエルゴ球よりも内側に存在することがわかります。
これらを図示したものが下図になります。この図では\(r_g = 1, a = 0.4\)などとして計算しています。
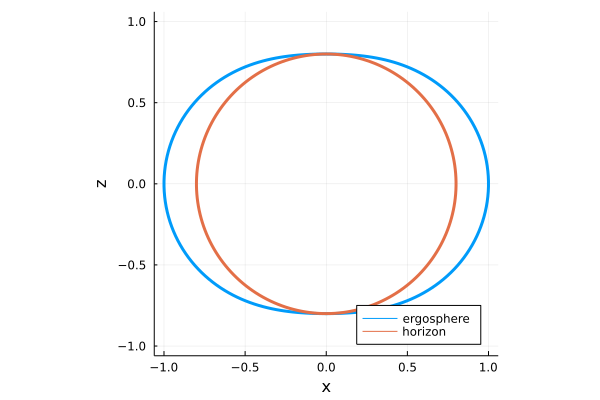
さらに次の図は\(r_g = 1, a = 0.45\)としたものです。
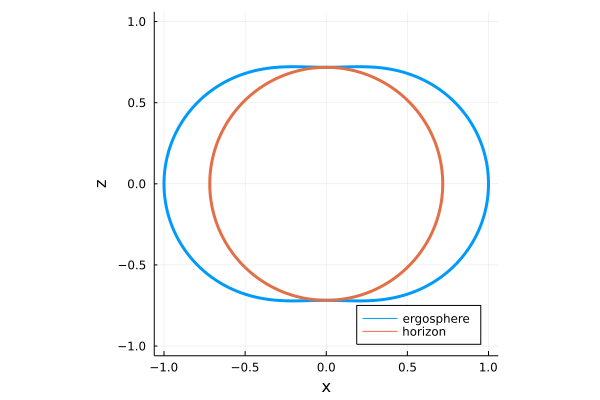
次にこの地平面の面積を計算します。 まずは\(r, t\)が一定となるような表面の面積を計算してみましょう。 \(dt = dr = 0\)より、(1)式から
\[ds^2 = \frac{(r^2+a^2)^2 - a^2 \Delta \sin^2 \theta}{\rho^2} \sin^2 \theta d\varphi^2 + \rho^2 d\theta^2 \tag{7}\]です。 ここから、面積積分の際に必要となる計量の行列式が
\[\sqrt{g} = \sqrt{\frac{(r^2+a^2)^2 - a^2 \Delta \sin^2 \theta}{\rho^2} \rho^2 } = \sqrt{(r^2+a^2)^2 - a^2 \Delta } \sin \theta \tag{8}\]のように求まります。
注意: マイナスがないのは、時間部分を考えていないためです。
これを\(\theta, \varphi\)で積分したものが面積となるので
\[A(r) = \int_0^\pi d\theta \int_0^{2\pi} d\varphi \sqrt{(r^2+a^2)^2 - a^2 \Delta } \sin \theta = 4\pi \sqrt{(r^2+a^2)^2 - a^2 \Delta } \tag{9}\]となります。 地平面においては\(\Delta = 0\)より
\[A(r_+) = 4\pi (r_+^2 + a^2) \tag{10}\]のように、最終的な計算結果を得ます。 (6)式から、\(r_+\)は\(r_g \propto M\)です。 よって、カーブラックホールの地平面の面積は\(M^2\)に比例することがわかります。
慣性系の引きずり
カー時空は軸対称性であり、方位角\(\varphi\)に依存しません。よって\(\varphi\)方向の単位質量あたりの角運動量を\(U_\varphi\)のように書くと、これは保存します。 ここで\(U_\varphi=0\)、すなわちカー・ブラックホールに突入する粒子の角速度を計算してみましょう。
\[\frac{d\varphi}{dt} = \frac{d\varphi}{d\tau} \frac{d\tau}{dt} = \frac{U^{\varphi}}{U^0 / c} = \frac{c (g^{\varphi \varphi} U_\varphi + g^{\varphi 0} U_0)}{g^{00} U_0 + g^{0\varphi} U_\varphi} = \frac{c g^{0 \varphi}}{g^{00}} \tag{11}\]この結果は、軌道角運動量がゼロだった粒子が、ブラックホールの自転による時空の引きずり効果で角速度を持つことを意味しています。 引きずりにより回転の向きはブラックホールの自転の向きと同じです。
参考文献
[1] 内山龍雄, “一般相対性理論”
[2] ランダウ, リフシッツ, “場の古典論”
[3] Schutz, “A First Course in General Relativity”