Table of contents
相対論的ビーミング
電磁波の輻射場の電場成分はリエナー・ブィーヒェルトポテンシャルから電磁場の導出より
\[{\bf E} = \frac{q}{c} \left[ \frac{\mathbf{n}\times ((\mathbf{n}-\boldsymbol{\beta})\times \dot{\boldsymbol{\beta}})}{\kappa^3 R}\right] \tag{*1}\]のように書けました。ここでは荷電粒子が相対論的な運動をしているとき、すなわち\(\gamma = \frac{1}{\sqrt{1-\beta^2}} \gg 1\)のときを考えましょう。さらに以下では\({\bf n}\cdot \boldsymbol{\beta}=\beta \cos \theta\)とします。
\(\kappa\)
\(\kappa\)を\(\theta\)の関数で表してみましょう。
\[\gamma = \frac{1}{\sqrt{1-\beta^2}} \ \Longrightarrow \ \beta = \sqrt{1- \frac{1}{\gamma^2}} \simeq 1 - \frac{1}{2 \gamma^2}\] \[\kappa(\theta) = 1- \beta \overbrace{\cos \theta}^{\simeq 1-\frac{\theta^2}{2}} \simeq 1- (1- \frac{\theta^2}{2} - \frac{1}{2\gamma^2} + \underbrace{\frac{\theta^2}{4\gamma^2}}_{\mathrm{negligible}}) \simeq \frac{\theta^2}{2} + \frac{1}{2\gamma^2} = \frac{1}{2\gamma^2} (\gamma^2 \theta^2 + 1) \tag{*2}\]\(\kappa\)は下図のような\(\theta\)の2次関数となります。
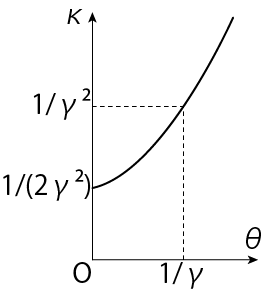
電場強度
\(\theta=0\)のとき、\(\boldsymbol{\beta}=\beta {\bf n}\)より\(\kappa(0) = 1-\beta\)なので
\[{\bf n} - \boldsymbol{\beta} = (1- \beta) {\bf n} = \kappa(0) {\bf n}\]よって(*1)より
\[{\bf E}_0 = \frac{q}{c} \left[ \frac{\mathbf{n} \times ( \kappa(0) \mathbf{n} \times \dot{\boldsymbol{\beta}}) }{\kappa(0)^3 R}\right] = \frac{q}{c} \left[ \frac{1}{\kappa(0)^2} \mathbf{n} \times (\mathbf{n} \times \dot{\boldsymbol{\beta}}) \right] = \frac{q}{c} \left[ \frac{1}{\kappa(0)^2} \left\{ (\mathbf{n} \cdot \dot{\boldsymbol{\beta}}) \mathbf{n} - \dot{\boldsymbol{\beta}} \right\} \right]\]\(\theta=\pi\)のとき、\(\boldsymbol{\beta}=- \beta \mathbf{n}\)より\(\kappa(\pi) = 1+\beta\)であるから、
\[{\bf n} - \boldsymbol{\beta} = (1+ \beta) {\bf n} = \kappa(\pi) {\bf n}\]より
\[{\bf E}_\pi = \frac{q}{c} \left[ \frac{\mathbf{n} \times ( - \kappa(\pi) \mathbf{n} \times \dot{\boldsymbol{\beta}} ) }{\kappa(\pi)^3 R}\right] = - \frac{q}{c} \left[ \frac{1}{\kappa(\pi)^2} \mathbf{n} \times (\mathbf{n} \times \dot{\boldsymbol{\beta}}) \right] = - \frac{q}{c} \left[ \frac{1}{\kappa(\pi)^2} \left\{ (\mathbf{n} \cdot \dot{\boldsymbol{\beta}}) \mathbf{n} - \dot{\boldsymbol{\beta}} \right\} \right]\] \[\therefore \ E_0 = \left[ \frac{\kappa(\pi)^2}{\kappa(0)^2}\right] E_\pi\] \[\left\{ \begin{array}{l} \kappa(0) = 1-\beta \simeq 1- (1-\frac{1}{2\gamma^2}) = \frac{1}{2\gamma^2} \\ \kappa(\pi) = 1+\beta \simeq 1+ (1-\frac{1}{2\gamma^2}) = 2-\frac{1}{2\gamma^2} \sim 2 \ (\gamma \gg 1 より) \end{array} \right.\] \[\therefore \ E_0 = \left[ 16 \gamma^4\right] E_\pi\]よって\(\theta = 0\)での電場強度は\(\theta = \pi\)の\(16\gamma^4\)倍であることがわかります。
放射強度の集中
\(\kappa\)は\(\theta\)の2次関数です。(*2)式の形より\(\theta< 1/\gamma\)では\(\kappa\)の増加が鈍く、\(\kappa>1/\gamma\)で\(\kappa\)は急激に増加します。(*1)式より\(\kappa\)の値が小さければ電場強度が大きくなるから、放射は\(\theta< 1/\gamma\)の角度に集中することがわかります。
時空図を用いた解釈
上述の結果を相対論的ビーミング効果(relativistic beaming effect)と呼びます。上図のような時空図からこの現象を説明してみましょう。
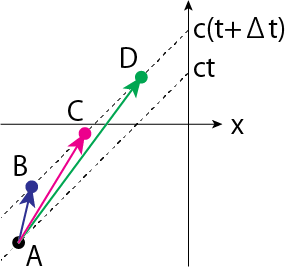
簡単のため電荷の運動は\(x\)方向のみとします。観測者は\(x=0\)に静止しているとします。点電荷の取りうる事象を\(A(ct_A, x_A)\), \(B(ct_B, x_B)\), \(C(ct_C, x_C)\), \(D(ct_D, x_D)\)のように書きましょう(ただし\(x_A<x_B<x_C<x_D\)かつ\(t_A<t_B<t_C<t_D\))。このとき、\(t \sim t+\Delta t\)に観測者が受け取ることが出来る電磁波はA->B、A->C、A->Dの間に電荷が発した電磁波です。電荷の速度が相対論的になり、時空図上をA->BでなくA->Dのように移動する場合には電磁波の届く量(電荷からの情報量)が多くなるために電磁波の強度が大きくなります。これが相対論的ビーミング効果の本質です。