HR図
HR (Hertzsprung-Russell)図は、恒星の進化を論ずるにあたって欠かせないものです。 縦軸は恒星の固有の明るさを示す量を表し、上に向かうほど明るくなるように取ります。 横軸は恒星の表面温度を表す量をとり、左から右に向かうほど温度が高くなるようにします。 様々な種類のHR図がありますが、大きく分けて観測的HR図と理論的HR図に分けられます。 観測的HR図では、縦軸に絶対等級が用いられ、横軸に色指数(二つの異なる波長域フィルターを通して測定された等級の差、例えば\(B - V\))が用いられるのが一般的です。 これは色等級図 (CM diagram)とも呼ばれます。 理論的HR図では、縦軸には光度 (luminosity) \(L\)、または全輻射等級 \(M_\mathrm{bol}\)が採用されます。 横軸には有効温度 (effective temperature \(T_\mathrm{eff}\))が取られます。 次の図は、理論的HR図の一例です。 縦軸には恒星の光度 \(L\)を太陽光度 \(L_\odot\)を単位としたものの対数値、横軸には有効温度の対数値が取られています。 有効温度とは、恒星が黒体輻射を出していると仮定したときの表面温度で、実際の表面温度の近似値となっています。 星の半径を\(R\)、光度を\(L\)とすると、有効温度は
\[L = 4\pi \sigma R^2 T_\mathrm{eff}^4 \qquad \mathrm{or} \qquad \frac{L}{L_\odot} = 8.973 \times 10^{-16} \left( \frac{R}{R_\odot}\right)^2 T_\mathrm{eff}^4 \tag{2.1.1}\]の関係があります。 すると
\[\log \frac{L}{L_\odot} = C + 2 \log \frac{R}{R_\odot} + 4 \log T_\mathrm{eff}\]よって、両対数グラフとして描かれるHR図では、半径一定の線は直線となります。 右上ほど半径の大きな天体が位置します。 ここで\(\sigma\)はStefan-Boltzmann’s constant (\(5.67 \times 10^{-5} [\mathrm{erg \ cm^{-2} \ K^{-4} \ s^{-1}}]\))です。
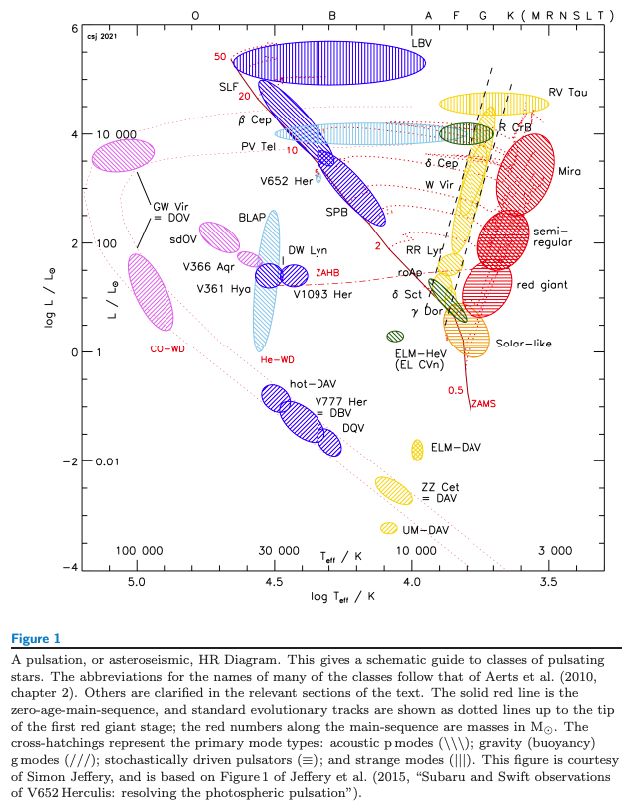
多くの星は、半径が\(1R_\odot\)を表す直線から少し傾いた主系列に存在します。 一方、太陽半径の100倍やそれ以上の大きさを持つものも存在し、それらは巨星(giants)や超巨星(super giants)と呼ばれます。 また、太陽半径の1/100程度の半径を持つ白色矮星(white dwarfs)も存在します。
光度と等級との関係は
で表されます。 光度は単位時間あたりに放出される全波長域でのエネルギーを表しているため、これが全輻射等級\(M_\mathrm{bol}\)に対応します。 実視絶対等級\(M_\mathrm{v}\)と全輻射等級とは
\[M_\mathrm{bol} = M_\mathrm{v} + B.C. \tag{2.1.3}\]のように関係づけられます。 ここで\(B.C.\)は全輻射補正 (bolometric correction)と呼ばれ、恒星の有効温度の関数です。 太陽に対しては、\(B.C._\odot = -0.07, M_\mathrm{bol, \odot} = 4.76\)とされています。 次の図は、縦軸に実視絶対等級、横軸にスペクトル型を採用した模式的なHR図です。 種族Iの星に対する主系列、および種々の光度階級 (luminosity class)の位置が記されています。
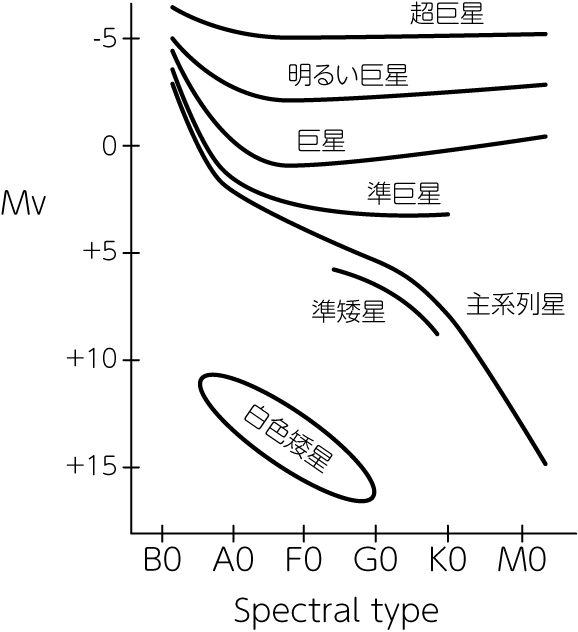
光度階級は、以下のように分類されています。
| ローマ数字 | 名称 |
|---|---|
| I | 超巨星 (supergiants) |
| II | 明るい巨星 (bright giants) |
| III | 巨星 (giants) |
| IV | 準巨星 (subgiants) |
| V | 主系列星 (main sequences) |
| VI | 準矮星 (subdwarfs) |
| VII | 白色矮星 (white dwarfs) |
天文学辞典の光度階級のページと日本語の名称が異なる部分があります。ひょっとしてここで示した呼び方は古いのかも?
参考文献
[1] Kurtz, 2022, “Asteroseismology across the HR diagram”
[2] 天文学辞典, 光度階級
[3] 野本憲一, 佐藤勝彦, 定金晃三, “シリーズ現代の天文学 恒星”