Table of contents
エルミート多項式 (Hermite polynomial)
級数表現
母関数展開
\[e^{2z\omega - \omega^2} = \sum_{n=0}^{\infty} \frac{H_n(z)}{n!} \omega^n \tag{1}\]のように定義される\(H_n(z)\)をエルミート多項式と呼びます。 この式の左辺は
\[e^{2z\omega - \omega^2} = e^{2z\omega} e^{-\omega^2} = \left( \sum_{\ell = 0}^\infty \frac{(2z\omega)^\ell}{\ell !} \right) \left( \sum_{m=0}^\infty \frac{(-\omega^2)^m}{m!}\right) = \sum_{\ell=0}^\infty \sum_{m=0}^\infty \frac{(-1)^m (2z)^\ell}{\ell ! m!} \omega^{\ell + 2m} \tag{2}\]のようにも計算されます。 ここで\(\ell + 2m = n \ (\ell = n-2m)\)とおくことで、\(\omega^n\)の形で整理を行いましょう。
\[e^{2z\omega - \omega^2} = \sum_{n=0}^\infty \sum_{m=0}^{[n/2]} \frac{(-1)^m (2z)^{n-2m}}{(n-2m)! m!} \omega^n = \sum_{n=0}^\infty \sum_{m=0}^{[n/2]} \frac{(-1)^m n! (2z)^{n-2m}}{(n-2m)! m!} \frac{\omega^n}{n!} \tag{3}\]これを(1)式と比較すると
\[H_n(z) = \sum_{m=0}^{[n/2]} \frac{(-1)^m n! (2z)^{n-2m}}{(n-2m)! m!} \tag{4}\]のような級数表現を得ます。
微分表現
(1)式の左辺において、\(z\)を固定して\(\omega\)に関してテイラー展開を行います。 すると\(\omega^n / n!\)の係数は
\[\begin{align} H_n (z) &= \left[ \frac{d^n}{d\omega^n} e^{2z\omega - \omega^2}\right]_{\omega = 0} = e^{z^2} \left[ \frac{d^n}{d\omega^n} e^{-(\omega - z)^2}\right]_{\omega = 0} \underbrace{=}_{u = \omega - z} e^{z^2} \left[ \frac{d^n}{du^n} e^{-u^2}\right]_{u = -z} = e^{z^2} \frac{d^n}{d(-z)^n} e^{-z^2} \notag \\ &= (-1)^n e^{z^2} \frac{d^n}{dz^n} e^{-z^2} \tag{5} \end{align}\]となり、微分系での表現も得ることができました。
多項式の直交性
直交性を考えるために、まずは以下の積分を計算しましょう。
\[\int_{-\infty}^\infty e^{2z\omega - \omega^2} e^{2zt - t^2} e^{-z^2} dz = \int_{-\infty}^\infty e^{-(z-\omega - t)^2} e^{2t\omega} dz \underbrace{=}_{ガウス積分} \sqrt{\pi} e^{2t\omega} = \sqrt{\pi} \sum_{n=0}^\infty \frac{(2t\omega)^n}{n!} \tag{6}\]ここで、(1)式より
\[e^{2z\omega - \omega^2} e^{2zt - t^2} = \sum_{n=0}^\infty \sum_{m=0}^\infty \frac{H_n H_m}{n! m!} \omega^n t^m \tag{7}\]が得られることから、これを(6)式に代入します。
\[\sum_{n=0}^\infty \sum_{m=0}^\infty \frac{\omega^n t^m}{n! m!} \int_{-\infty}^\infty H_n H_m e^{-z^2} dz = \sqrt{\pi} \sum_{n=0}^\infty \frac{2^n \omega^n t^n}{n!} = \sqrt{\pi} \sum_{n=0}^\infty \sum_{m=0}^\infty \frac{2^n \omega^n t^m}{n! m!} m! \delta_{nm} \tag{8}\]両辺の\(\omega, t\)のベキの係数を比較することで
\[\int_{-\infty}^\infty H_n H_m e^{-z^2} dz = 2^n n! \sqrt{\pi} \delta_{nm} \tag{9}\]という直交性が導かれます。
漸化式
エルミート多項式が満たす漸化式をいくつか証明しましょう。 (1)式の両辺を\(z\)微分したものより
\[2\omega e^{2z\omega - \omega^2} = \sum_{n=0}^\infty \frac{H_n'}{n!} \omega^n \tag{10}\]この左辺は
\[2\omega e^{2z\omega - \omega^2} = 2\omega \sum_{n=0}^\infty \frac{H_n}{n!} \omega^n = \sum_{n=0}^\infty \frac{2 H_n}{n!} \omega^{n+1} = \sum_{n=1}^\infty \frac{2 H_{n-1}}{(n-1)!} \omega^n \tag{11}\]のように変形されるので、\(\omega^n\)の係数比較から
\[\frac{H_n'}{n!} = \frac{2H_{n-1}}{(n-1)!} \ \Longrightarrow \ H_n' = 2n H_{n-1} \quad (n \geq 1) \tag{12}\]を得ます。 さらに(1)式の両辺を\(\omega\)微分すると
\[2(z-\omega) e^{2z\omega - \omega^2} = \sum_{n=1}^\infty \frac{H_n}{(n-1)!} \omega^{n-1} = \sum_{n=0}^\infty \frac{H_{n+1}}{n!} \omega^n \tag{13}\]この最左辺は
\[2(z-\omega) e^{2z\omega - \omega^2} = 2z \sum_{n=0}^\infty \frac{H_n}{n!} \omega^n - 2 \sum_{n=0}^\infty \frac{H_n}{n!} \omega^{n+1} = 2z \sum_{n=0}^\infty \frac{H_n}{n!} \omega^n - 2 \sum_{n=1}^\infty \frac{H_{n-1}}{(n-1)!} \omega^{n} \tag{14}\]のように変形されるので、\(\omega^n\)の係数比較から
\[\frac{H_{n+1}}{n!} = \frac{2zH_n}{n!} - \frac{2H_{n-1}}{(n-1)!} \ \Longrightarrow \ H_{n+1} = 2z H_n - 2n H_{n-1} \quad (n \geq 1) \tag{15}\]となります。
(5)式の両辺を\(z\)微分すると
となります。 さらに両辺を\(z\)微分すれば
\[H_n'' = 2H_n + 2z H_n' - H_{n+1}' \tag{17}\]を得ます。 そして(12)式より\(H_{n+1}' = 2(n+1) H_n\)を用いると
\[H_n'' = 2H_n + 2z H_n' - 2(n+1) H_n = 2z H_n' - 2n H_n \ \Longrightarrow \ H_n'' - 2z H_n' + 2nH_n = 0 \tag{18}\]を導くことができます。 これをエルミートの微分方程式と呼びます。
エルミート多項式の具体的な形
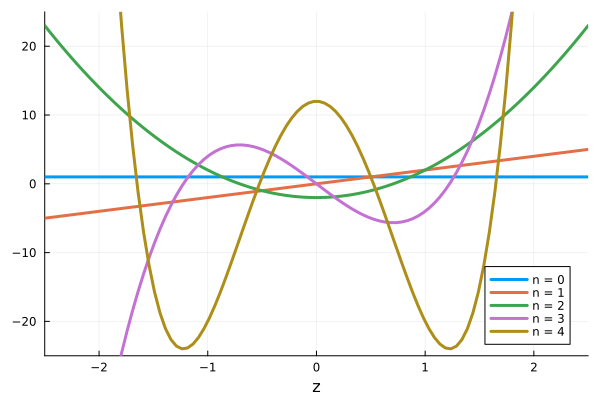
以下に、いくつかのエルミート多項式の具体的な形を示します。
\[\begin{align} &H_0(z) = 1, \quad H_1(z) = 2z, \quad H_2(z) = 4z^2 - 2, \quad H_3(z) = 8z^3 - 12z, \notag \\ &H_4(z) = 16z^4 - 48z^2 + 12, \quad H_5(z) = 32z^5 - 160z^3 + 120z \tag{19} \end{align}\]また、いくつかのエルミート多項式を可視化したものを示します。
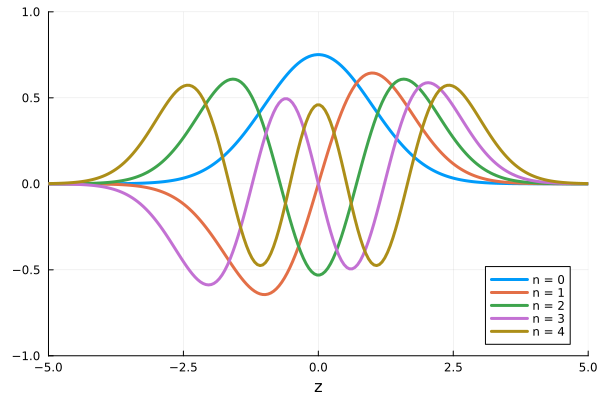
さらにより馴染みのあるものとして、量子力学の1次元調和振動子の固有関数を可視化してみました。 調和振動子ポテンシャル中における粒子の波動関数は、以下のように書けます。
\[\phi_n (\xi) = \frac{1}{\sqrt{2^n n! \sqrt{\pi}}} H_n (\xi) e^{-\xi^2 / 2} \tag{20}\]規格化定数は、先程の直交性(9)式から求めることができます。
この描画に用いたJuliaスクリプトを以下に示します。
using SpecialPolynomials
using Plots
gr()
# set z-coordinate
len_z = 200
min_z = -5.0
max_z = 5.0
array_z = range(min_z, max_z, length=len_z)
# set empty plot
plt = plot()
for n in 0:4
# make Hermite polynomial basis for specific n
h = Basis(Hermite, n)
# compute wavefunction of 1-d harmonic oscillator
psi = 1.0 / sqrt(sqrt(pi)*2^n*factorial(n)) .* h.(array_z) .* exp.(-array_z.^2 / 2)
# make string for plot label
index = "n = " * string(n)
# compute Hermite polynomial and make plots
plot!(plt, array_z, psi, linewidth=3, xlims=(min_z, max_z), ylims=(-1.0, 1.0), xlabel="z", label=index)
end
# save plot figure
savefig("hermite_02.png")
参考文献
[1] 田島, 近藤, “改訂演習工科の数学4, 複素関数”
[2] 中山, “裳華房フィジックスライブリー, 物理数学II”
[3] 福山, 小形, “基礎物理学シリーズ3, 物理数学I”
[4] 猪木慶治, 川合光, “量子力学 I”