リエナー・ブィーヒェルトポテンシャルからの電磁場導出
時空図を用いた議論
時間偏微分
時空図上で\(x\)座標を固定して考えることで、電磁場を計算するための時間微分を導出しましょう。当然ですが、\(\frac{\partial}{\partial t}\)とは観測者の座標\(\mathbf{r}\)を固定して観測者の時間\(t\)のみ変化させたときの物理量の変化を計算しなさい、という意味です。微分される関数は\(\boldsymbol{\beta}, R(t'), \kappa (t')\)です。これらは\(t\)をあらわに含みませんが、\(t\)の変化に伴う\(t'\)の変化を通して\(t\)に依存します。そこで\(t\)の偏微分から\(t'\)の偏微分への変換を行います。以下のように時空図に\(t\)の変化に伴う荷電粒子の位置の変化と\(t'\)の変化の様子を表します。
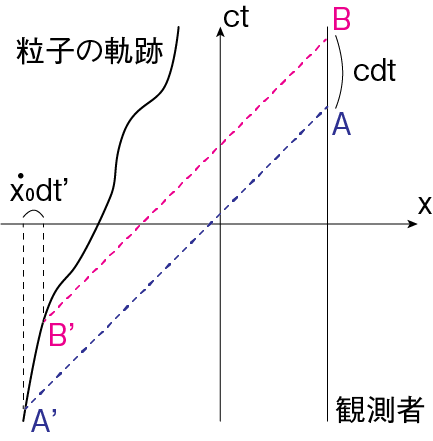
上図では簡単のため、系は空間1次元としました。観測者は座標\(x\)の位置に静止しています。時刻\(t\)の観測者の事象Aと微小時間\(dt\)後の観測者の事象Bとそれぞれ観測した電磁ポテンシャルの差分をとり、\(dt\)で割る操作が\(t\)による偏微分となります。グリーン関数の性質より、ある時空点に存在した点電荷が電磁場へ与える影響は光速度\(c\)で等方的に伝播していきます。したがって事象A, Bで観測される電磁場は、事象A’, B’にいた電荷によって生成されたものとなります。
事象AとA’の時刻の関係は\(t=t'+|\mathbf{r}−\mathbf{r}_0|/c\)で与えられます。同様に事象BとB’の時刻の関係は\(t+dt=t'+dt'+|\mathbf{r}−\mathbf{r}_0(t'+dt')|/c\)となります。この二つの事象間での観測者から粒子までの距離の変化量は、この間の粒子の運動により粒子が観測者に近づいた距離に等しいので\(|\mathbf{r}−\mathbf{r}_0(t'+dt')|−|\mathbf{r}−\mathbf{r}_0(t')|=−\mathbf{u}(t') \cdot \mathbf{n}(t')dt'\)と与えられます。以上より\(dt\)と\(dt'\)の関係は以下のように計算できます。
したがって、偏微分の変換式は
\[\frac{\partial }{\partial t} = \frac{1}{\kappa (t')} \frac{\partial }{\partial t'} \tag{2}\]となります。
ドップラー効果
(1)のの関係式はドップラー効果からも導出することができます。
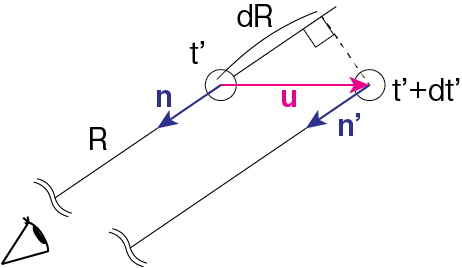
時刻\(t'\)における荷電粒子と観測者との距離を\(R\)としましょう。上図のように考えます。\(dt'\)は微小として、\(\mathbf{n} \simeq \mathbf{n}'\)とします。微小時間\(dt'\)での観測者から粒子までの距離の変化は\(\mathbf{u} dt'\)を観測者の視線方向へ射影したものです。よって距離変化\(dR\)は
\[dR = - \mathbf{n} \cdot \mathbf{u} dt'\]です。時刻\(t'\)に放たれた電磁波を観測者が時刻\(t\)に受け取ったとすると
\[t = t' + \frac{R}{c}\]そして\(t' + dt'\)に放たれた電磁波を観測者が時刻\(t+dt\)に受け取ったとすれば
\[t + dt = t' + dt' + \frac{R + dR}{c}\]以上より
\[dt = \left( t' + dt' + \frac{R+dR}{c} \right) - \left( t' + \frac{R}{c} \right) = dt' + \frac{dR}{c} = \left( 1- \frac{\mathbf{n} \cdot \mathbf{u}}{c} \right) dt'\]となり、(1)式と一致することがわかります。
空間偏微分
次に\(\frac{\partial }{\partial \mathbf{r}}\)について考えましょう。この演算は事象Aにいる観測者と同時刻\(t\)で微小距離\(d\mathbf{r}\)離れた事象Cにいる観測者で、それぞれ測定した電磁ポテンシャルの勾配を求めることに対応します。ここでも時空図は簡単のため空間一次元を示しました。
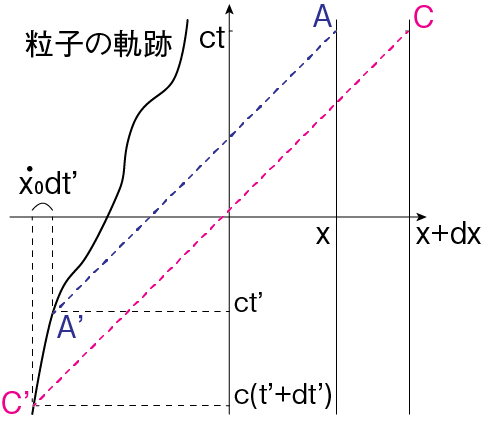
事象Cで観測される電磁場は事象C’にいた電荷によって生成されたものです。事象Aと事象Cで観測が行われる時刻は同じ\(t\)ですが、それぞれで観測される電磁場が生成された時刻・場所は異なることがわかります。事象Cの観測者から事象C’の粒子までの距離と、事象Aの観測者から事象A’の粒子のまでの距離の差は、\(dt′\)間の粒子の運動により粒子が観測者に近づいた分短くなった距離とCがAより\(d\mathbf{r}\)だけ離れていることから\(d \mathbf{r} \cdot \mathbf{n}\)だけもともと離れている効果の足し合わせとなります。 したがって\(|\mathbf{r}+d \mathbf{r}−\mathbf{r}_0(t'+dt')|−| \mathbf{r}−\mathbf{r}_0(t)| = d\mathbf{r} \cdot \mathbf{n}−\mathbf{u}(t') \cdot \mathbf{n}(t')dt'\)となります。先ほどと同様に、事象AとA’およびCとC’のそれぞれの時間関係
\[t_A = t' + \frac{|\mathbf{r}-\mathbf{r}_0 (t')|}{c} \tag{3}\] \[t_C = t' +dt' + \frac{|\mathbf{r} + d\mathbf{r} - \mathbf{r}_0 (t'+dt')|}{c} \tag{4}\]より
\[\begin{align} &dt' = -\frac{1}{c} (|\mathbf{r} + d\mathbf{r}-\mathbf{r}_0 (t'+dt')| - |\mathbf{r}-\mathbf{r}_0 (t')|) = - \frac{d\mathbf{r} \cdot \mathbf{n}-\mathbf{u}(t')\cdot \mathbf{n}(t') dt'}{c} \notag \\ &\Longrightarrow \ \frac{\partial t'}{\partial \mathbf{r}} = - \frac{1}{\kappa (t') c} \mathbf{n} \ \Longrightarrow \ \therefore \ \frac{\partial }{\partial \mathbf{r}} = - \frac{\mathbf{n} (t')}{c \kappa (t')} \frac{\partial }{\partial t'} \tag{5} \end{align}\]ただし\(R(t'), \mathbf{R} (t')\)に\(\frac{\partial}{\partial \mathbf{r}}\)を作用させるとき、これらは\(\mathbf{r}\)にも依存しています。よって連鎖律より
\[\frac{\partial }{\partial \mathbf{r}} = \left( \frac{\partial}{\partial \mathbf{r}}\right)_{\mathbf{r}_0} - \frac{\mathbf{n} (t')}{c \kappa (t')} \frac{\partial }{\partial t'} \tag{6}\]この式の第1項は\(\mathbf{r}_0\)を一定にして\(\mathbf{r}\)微分を行う、という意味です。
電磁場の導出
以上の式を用いて、リエナー・ヴィーヒェルトポテンシャルから運動する1個の点電荷が作る電場・磁場を計算しましょう。
以降の計算では、これまでの偏微分で現れた\(t'\)を\(t_\mathrm{ret}\)と置き換えて計算を行います。
ここで\([Q]\)は遅延時間での物理量\(Q\)の値を使いなさい、という記号です。マクスウェル方程式より
\[\mathbf{E} (\mathbf{r}, t) = - \nabla \phi - \frac{1}{c} \frac{\partial \mathbf{A}}{\partial t} \tag{9}\] \[\mathbf{B} (\mathbf{r}, t) = \nabla \times \mathbf{A} \tag{10}\](2)式より
\[\frac{\partial }{\partial t} [\kappa R] = \frac{1}{\kappa (t_\mathrm{ret})} \frac{\partial}{\partial t_\mathrm{ret}} [\kappa R] = \left[ \frac{1}{\kappa} \left( R \frac{\partial \kappa}{\partial t} + \kappa \frac{\partial R}{\partial t}\right) \right]\] \[\left[ \frac{\partial R}{\partial t}\right] = \left[ \frac{\mathbf{R}}{R} \cdot (- \mathbf{u})\right] = -c [\mathbf{n} \cdot \boldsymbol{\beta}]\] \[\begin{align} \left[ \frac{\partial \kappa}{\partial t} \right] &= \left[ \frac{\partial}{\partial t} (1-\mathbf{n} \cdot \boldsymbol{\beta})\right] = - \left[ \frac{\partial \mathbf{n}}{\partial t} \cdot \boldsymbol{\beta} + \mathbf{n} \cdot \frac{\partial \boldsymbol{\beta}}{\partial t} \right] = - \left[ \frac{(- \mathbf{u}) R - \mathbf{R} (-c \mathbf{n} \cdot \boldsymbol{\beta})}{R^2} \cdot \boldsymbol{\beta} + \mathbf{n} \cdot \dot{\boldsymbol{\beta}}\right] \notag \\ &= \left[ \frac{c}{R} \beta^2 - \frac{c}{R} (\mathbf{n} \cdot \boldsymbol{\beta})^2 - \mathbf{n} \cdot \dot{\boldsymbol{\beta}} \right] \notag \end{align}\]以上より
\[\begin{align} \frac{\partial }{\partial t} [\kappa R] &= \left[ \frac{1}{\kappa} (c\beta^2 - c (\mathbf{n} \cdot \boldsymbol{\beta})^2 - R \mathbf{n} \cdot \dot{\boldsymbol{\beta}}- c \kappa \mathbf{n} \cdot \boldsymbol{\beta})\right] = \left[ \frac{c}{\kappa} \beta^2 - \frac{c}{\kappa} (\mathbf{n} \cdot \boldsymbol{\beta}) (\mathbf{n} \cdot \boldsymbol{\beta} + \kappa) - \frac{R}{\kappa} \mathbf{n} \cdot \dot{\boldsymbol{\beta}} \right] \notag \\ &= \left[ \frac{c}{\kappa} \beta^2 - \frac{c}{\kappa} \mathbf{n} \cdot \boldsymbol{\beta} - \frac{R}{\kappa} \mathbf{n} \cdot \dot{\boldsymbol{\beta}} \right] \tag{11} \end{align}\]また(6)式より
\[\nabla [\kappa R] = \left[ \left\{ \left( \frac{\partial R}{\partial \mathbf{r}} \right)_{\mathbf{r}_0} - \frac{\mathbf{n}}{c\kappa} \frac{\partial R}{\partial t}\right\} \kappa + R \left\{ \left( \frac{\partial \kappa}{\partial \mathbf{r}}\right)_{\mathbf{r}_0} - \frac{\mathbf{n}}{c \kappa} \frac{\partial \kappa}{\partial t}\right\} \right]\] \[\left[ \left( \frac{\partial R}{\partial \mathbf{r}}\right)_{\mathbf{r}_0} \right] = \left[ \frac{\mathbf{R}}{R} \right] = \left[ \mathbf{n} \right]\] \[\left[ \left( \frac{\partial \kappa}{\partial \mathbf{r}}\right)_{\mathbf{r}_0} \right] = - \left[ \frac{\boldsymbol{\beta}}{R} - \frac{\mathbf{R} \cdot \boldsymbol{\beta}}{R^3} \mathbf{R} \right] = - \left[ \frac{\boldsymbol{\beta}}{R} - \frac{\mathbf{n} \cdot \boldsymbol{\beta}}{R} \mathbf{n} \right]\]以上より
\[\begin{align} \nabla [\kappa R] &= \left[ \left\{ \mathbf{n} - \frac{\mathbf{n}}{c \kappa} (-c \mathbf{n} \cdot \boldsymbol{\beta}) \right\} \kappa + R \left\{ -\frac{\boldsymbol{\beta}}{R} + \frac{\mathbf{n} \cdot \boldsymbol{\beta}}{R} \mathbf{n} - \frac{\mathbf{n}}{c \kappa} \left( \frac{c}{R} \beta^2 - \frac{c}{R} (\mathbf{n} \cdot \boldsymbol{\beta})^2 - \mathbf{n} \cdot \dot{\boldsymbol{\beta}}\right) \right\} \right] \notag \\ &= \left[ \kappa \mathbf{n} + (\mathbf{n} \cdot \boldsymbol{\beta}) \mathbf{n} - \boldsymbol{\beta} + (\mathbf{n} \cdot \boldsymbol{\beta}) \mathbf{n} - \frac{\beta^2}{\kappa} \mathbf{n} + \frac{(\mathbf{n} \cdot \boldsymbol{\beta})^2}{\kappa} \mathbf{n} + \frac{R (\mathbf{n} \cdot \dot{\boldsymbol{\beta}})}{c\kappa} \mathbf{n}\right] \notag \\ &= \left[ \mathbf{n} - \boldsymbol{\beta} + \frac{\kappa (\mathbf{n} \cdot \boldsymbol{\beta}) + (\mathbf{n} \cdot \boldsymbol{\beta})^2}{\kappa} \mathbf{n} - \frac{\beta^2}{\kappa} \mathbf{n} + \frac{R (\mathbf{n} \cdot \dot{\boldsymbol{\beta}})}{c \kappa} \mathbf{n} \right] \notag \\ &= \left[ \mathbf{n} - \boldsymbol{\beta} + \frac{\mathbf{n} \cdot \boldsymbol{\beta}}{\kappa} \mathbf{n} - \frac{\beta^2}{\kappa} \mathbf{n} + \frac{R (\mathbf{n} \cdot \dot{\boldsymbol{\beta}})}{c \kappa} \mathbf{n}\right] \notag \end{align}\]よって
\[\begin{align} \mathbf{E} (\mathbf{r}, t) &= - \nabla \left[ \frac{q}{\kappa R}\right] -\frac{1}{c} \frac{\partial}{\partial t} \left[ \frac{q \boldsymbol{\beta}}{\kappa R}\right] \notag \\ &= -q \left[ \frac{- \left( \mathbf{n} - \boldsymbol{\beta} + \frac{(\mathbf{n} \cdot \boldsymbol{\beta})}{\kappa} \mathbf{n} - \frac{\beta^2}{\kappa} \mathbf{n} + \frac{R}{c \kappa} (\mathbf{n} \cdot \dot{\boldsymbol{\beta}}) \mathbf{n} \right)}{(\kappa R)^2}\right] - \frac{q}{c} \left[ \frac{\frac{1}{\kappa} \dot{\boldsymbol{\beta}} \kappa R - \boldsymbol{\beta} \left( \frac{c}{\kappa} \beta^2 - \frac{c}{\kappa} \mathbf{n} \cdot \boldsymbol{\beta} - \frac{R}{\kappa} \mathbf{n} \cdot \dot{\boldsymbol{\beta}} \right)}{(\kappa R)^2}\right] \notag \\ &= q \left[ \frac{\kappa (\mathbf{n} - \boldsymbol{\beta}) + (\mathbf{n} \cdot \boldsymbol{\beta}) \mathbf{n} - \beta^2 \mathbf{n}}{\kappa^3 R^2} + \frac{\mathbf{n} \cdot \dot{\boldsymbol{\beta}}}{c\kappa^3R} \mathbf{n} \right] - \frac{q}{c} \left[ \frac{1}{\kappa^2 R} \dot{\boldsymbol{\beta}} - \frac{c}{\kappa^3 R^2} (\beta^2 - \mathbf{n} \cdot \boldsymbol{\beta}) \boldsymbol{\beta} + \frac{\mathbf{n} \cdot \dot{\boldsymbol{\beta}}}{\kappa^3 R} \boldsymbol{\beta}\right] \notag \\ &= q \left[ \frac{\kappa (\mathbf{n} - \boldsymbol{\beta}) + (\mathbf{n} \cdot \boldsymbol{\beta}) \mathbf{n} - \beta^2 \mathbf{n} + (\beta^2 - \mathbf{n} \cdot \boldsymbol{\beta}) \boldsymbol{\beta}}{\kappa^3 R^2}\right] + \frac{q}{c} \left[ \frac{(\mathbf{n} \cdot \dot{\boldsymbol{\beta}}) \mathbf{n} - \kappa \dot{\boldsymbol{\beta}} - (\mathbf{n} \cdot \dot{\boldsymbol{\beta}}) \boldsymbol{\beta}}{\kappa^3 R}\right] \notag \\ &= q \left[ \frac{\mathbf{n} - \boldsymbol{\beta} - \beta^2 \mathbf{n}+\beta^2 \boldsymbol{\beta}}{\kappa^3 R^2} \right] + \frac{q}{c} \left[ \frac{(\mathbf{n} \cdot \dot{\boldsymbol{\beta}}) \mathbf{n} - \kappa \dot{\boldsymbol{\beta}} - (\mathbf{n} \cdot \dot{\boldsymbol{\beta}}) \boldsymbol{\beta}}{\kappa^3 R}\right] \notag \\ &= q \left[ \frac{(1-\beta^2)(\mathbf{n}- \boldsymbol{\beta})}{\kappa^3 R^2}\right] + \frac{q}{c} \left[ \frac{(\mathbf{n} \cdot \dot{\boldsymbol{\beta}}) \mathbf{n} - \kappa \dot{\boldsymbol{\beta}} - (\mathbf{n} \cdot \dot{\boldsymbol{\beta}}) \boldsymbol{\beta}}{\kappa^3 R}\right] \notag \end{align}\]ここで
\[\mathbf{n} \{ (\mathbf{n} - \boldsymbol{\beta}) \times \dot{\boldsymbol{\beta}} \} = (\mathbf{n} \cdot \dot{\boldsymbol{\beta}}) (\mathbf{n} - \boldsymbol{\beta}) - \{ \mathbf{n} \cdot (\mathbf{n}- \boldsymbol{\beta}) \} \dot{\boldsymbol{\beta}} = (\mathbf{n} \cdot \dot{\boldsymbol{\beta}}) (\mathbf{n}- \boldsymbol{\beta}) - \kappa \dot{\boldsymbol{\beta}}\]より
\[\mathbf{E} (\mathbf{r}, t) = q \left[ \frac{(1-\beta^2) (\mathbf{n}-\boldsymbol{\beta})}{\kappa^3 R^2}\right] + \frac{q}{c} \left[ \frac{\mathbf{n} \times \{ (\mathbf{n} - \boldsymbol{\beta}) \times \dot{\boldsymbol{\beta}} \}}{\kappa^3 R}\right] \tag{12}\]次に磁場を求めましょう。
\[\mathbf{B} = \nabla \times \mathbf{A} = \nabla \times [\phi \boldsymbol{\beta}] = \left[ \left( \frac{\partial}{\partial \mathbf{r}}\right)_{\mathbf{r}_0} \times (\phi \boldsymbol{\beta}) - \mathbf{n} \times \left( \frac{1}{c \kappa} \frac{\partial}{\partial t} (\phi \boldsymbol{\beta})\right) \right]\]ここでベクトル恒等式より
\[\begin{align} \left( \frac{\partial}{\partial \mathbf{r}}\right)_{\mathbf{r}_0} \times (\phi \boldsymbol{\beta}) &= \left( \frac{\partial \phi}{\partial \mathbf{r}} \right)_{\mathbf{r}_0} \times \boldsymbol{\beta} + \phi \underbrace{\left( \frac{\partial}{\partial \mathbf{r}} \right)_{\mathbf{r}_0} \times \boldsymbol{\beta}}_{=\mathbf{0}} = \left\{ - \frac{q}{(\kappa R)^2} \left( \frac{\partial}{\partial \mathbf{r}}\right)_{\mathbf{r}_0} (R- \mathbf{R} \cdot \boldsymbol{\beta})\right\} \times \boldsymbol{\beta} \notag \\ &= - \frac{q}{(\kappa R)^2} (\mathbf{n} - \boldsymbol{\beta}) \times \boldsymbol{\beta} = - \frac{q}{(\kappa R)^2} (\mathbf{n} \times \boldsymbol{\beta}) \notag \end{align}\]途中、\(\boldsymbol{\beta} = \frac{1}{c} \frac{d \mathbf{r}_0}{dt}\)から、\(\mathbf{r}_0\)を固定した微分は0としました。よって
\[\mathbf{B} (\mathbf{r}, t) = - \left[ \frac{q}{(\kappa R)^2} \mathbf{n} \times \boldsymbol{\beta} + \mathbf{n} \times \left( \frac{1}{c\kappa} \frac{\partial}{\partial t} (\phi \boldsymbol{\beta}) \right)\right]\]一方で、(12)式より
\[\begin{align} [\mathbf{n} \times \mathbf{E}] &= - [\mathbf{n}] \times \nabla \phi + \frac{1}{c} [\mathbf{n}] \times \frac{\partial \mathbf{A}}{\partial t} = - \left[ \mathbf{n} \times \left\{ \left( \frac{\partial \phi}{\partial \mathbf{r}}\right)_{\mathbf{r}_0} - \frac{\mathbf{n}}{c \kappa} \frac{\partial \phi}{\partial t} \right\} + \mathbf{n} \times \left( \frac{1}{c\kappa} \frac{\partial}{\partial t} (\phi \boldsymbol{\beta})\right)\right] \notag \\ &= - \left[ \mathbf{n} \times \left\{ - \frac{q}{(\kappa R)^2} (\mathbf{n} - \boldsymbol{\beta})\right\} + \mathbf{n} \times \left( \frac{1}{c\kappa} \frac{\partial }{\partial t} (\phi \boldsymbol{\beta})\right)\right] = - \left[ \frac{q}{(\kappa R)^2} \mathbf{n} \times \boldsymbol{\beta} + \mathbf{n} \times \left( \frac{1}{c\kappa} \frac{\partial }{\partial t} (\phi \boldsymbol{\beta})\right)\right] \notag \end{align}\]これらより
\[\mathbf{B} (\mathbf{r}, t) = [\mathbf{n} \times \mathbf{E}] \tag{13}\]と求まります。