Table of contents
ファラデートモグラフィ
ここでは近年の電波観測の発展に伴って注目されつつある、新しい宇宙物理解析手法のファラデートモグラフィ (Faraday tomography)についてご紹介します。
トモグラフィとは
トモグラフィとは様々な方向からの多数の投影データを用いて、対象とする物体の立体構造を把握するような技術のことです。 X線CTや地震波トモグラフィなどが有名な応用例として知られています。 例えばX線CTでは、発生器から放射されるX線を様々な角度から人体に照射します。 その反対側にX線検出器を置き、X線がどの程度吸収されたか、あるいは吸収されずに透過してきたかを観測します。 検出器が受け取る信号の情報は一次元に圧縮されたものです。 例えば、X線源から放射された強度の半分が観測されたとしましょう。 すると半分のX線は吸収されたと考えられるわけですが、それには下図のようにいくつもの組合せが考えられます。
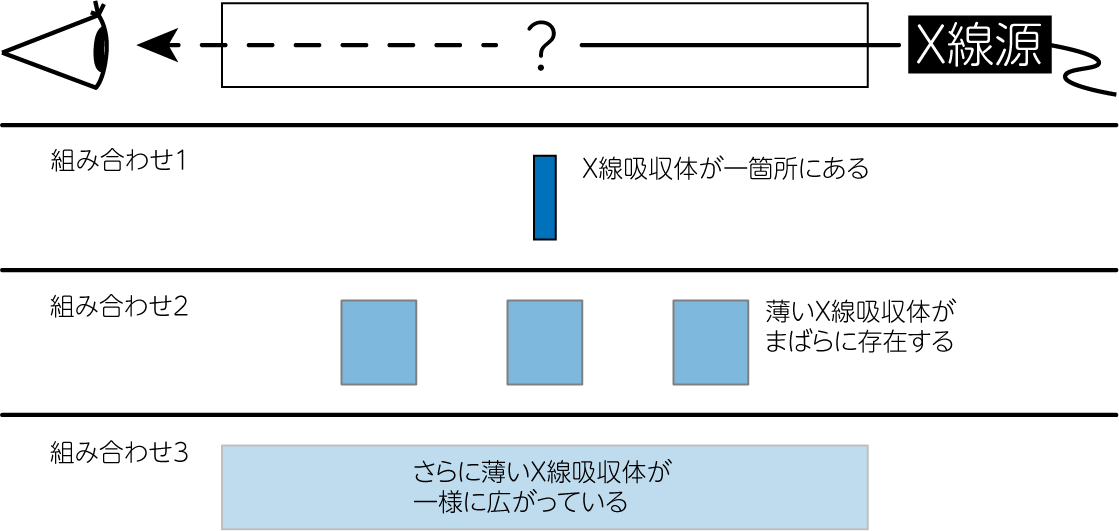
この中から一意に構造を決定するために、様々な方向からX線を照射し、これを2次元データにします。 それをフーリエ変換による一連の技術により、元の構造を復元するのがX線CTの原理です。
ファラデートモグラフィ (Faraday tomography)
ではファラデートモグラフィとはどのようなものでしょうか。 磁場を伴うプラズマ中を直線偏光電磁波が通過すると、ファラデー回転によりその偏光方向が変化します。 このとき、ファラデー回転による偏光方向の変化\(\Delta \theta\)は
\[\Delta \theta = \mathrm{RM} \lambda^2 \quad \left( \mathrm{RM} = 0.81 \int_\mathrm{source}^\mathrm{observer} n_e B_\parallel ds \ [\mathrm{rad \cdot m}^{-2}]\right) \tag{1}\]のように書かれるのでした。 ここでRM (Rotation Measure: 回転量度)は、電子数密度\(n_e\)は\(\mathrm{cm}^{-3}\)、観測者の視線方向に沿った磁場の成分\(B_\parallel\)は\(\mu \mathrm{G}\)、そして\(ds\)はpcの単位で計算されるものとします。 ここから、ファラデー回転を受ける前の初期偏光角を\(\chi_0\)、そして観測者が観測する偏光角を\(\chi\)とすると
\[\chi = \chi_0 + \mathrm{RM} \lambda^2 \tag{2}\]のようになります。 縦軸に偏光角\(\chi\)、横軸に\(\lambda^2\)の図を描けば、RMを傾きとする直線になることがわかります。 しかし(1)式を見ると、RMは視線方向に\(n_e B_\parallel\)を積分したものになっています。 よって複雑に\(n_e, B_\parallel\)が変化する乱流のような場合や、複数の天体が視線方向に存在するような場合には、このような直線の推定は困難となります。 このような複雑な構造の場合にも、磁場の構造や電子数密度の情報を正確に求めるために開発された技術が、ファラデートモグラフィです。
ファラデートモグラフィの代表的手法
ファラデートモグラフィの最終的な目的は、ファラデー回転の観測結果から磁場と偏波源などの空間情報(正確には視線方向分布)を引き出すことです。 この目的を叶える主要な手法は大きく分けて2つあります。
- RM synthesis (回転度量合成)
- QU-fitting
以下では、この代表的な2つの手法についてご説明します。
RM synthesisの原理
ここまでRMを用いてきましたが、以降ではこれを\(\phi\)のように表記し、これをファラデー深度(Faraday depth)と呼ぶことにしましょう。 深度と言っていますが、これは正負どちらもとることが出来る量です。 ファラデー深度が正の場合、磁場は観測者に向かう方向を持ち、負ならば遠ざかる方向の磁場を意味します。 またここからFaraday thin, Faraday thickなどの概念も考えることができます。 Faraday thinである、とは(2)式において\(\lambda^2 \Delta \phi \ll 1\)のように、ファラデー回転による偏光角の変化がとても小さい場合を意味します。 ここで\(\Delta \phi\)は\(\phi\)空間において天体の広がりを表しています。 もしFaraday thinならば、デルタ関数的に近似することができるでしょう。 逆にFaraday thickとは\(\lambda^2 \Delta \phi \gg 1\)であり、これは\(\phi\)空間において広がりのある天体を意味します。
直線偏光の偏光角を考えるため、以下では円偏光は考えないものとします。 すなわち、ストークスパラメータにおいて\(V = 0\)とします。 すると複素偏光強度から、この直線偏光を
のように特徴づけることができます。 ここで\(p\)は部分偏光を表す変数で、無偏光の場合には\(p=0\)、完全偏光の場合には\(p=1\)となるようなものです。 またこれらは観測波長\(\lambda\)に依存しますが、(2)式と合わせるため、そして波長は常に正の値しか取らないことから、\(\lambda^2\)の関数であるとしています(後述も参照。)
Faraday Dispersion Function (FDF: ファラデー分散関数)
(3)式をフーリエ積分表示したものを考えます。
\[P(\lambda^2) = \int_{-\infty}^\infty F(\phi) e^{2i\phi \lambda^2} d\phi \tag{4}\]ここで出てきた\(F(\phi)\)をファラデー分散関数と呼びます。 これは\(\phi\)空間における複素偏光強度の分布を表しています。 下図は、例えば遠方の電波源から偏波を観測した場合の\(F(\phi)\)を簡略化して描いたものです。 簡単のため、偏波源から天の川銀河までの間の空間には、磁場やプラズマは存在しないとしています。 偏波源から出た電磁波はある偏光角で放出されると考えられるため、ある\(\phi\)にデルタ関数的なピークを持ちます。 しかし、天の川銀河のような磁場を含む星間物質が存在する箇所では、偏波はファラデー回転を受けます。 これによりある\(\phi\)の領域にも\(F(\phi)\)が存在するような関数形となります。
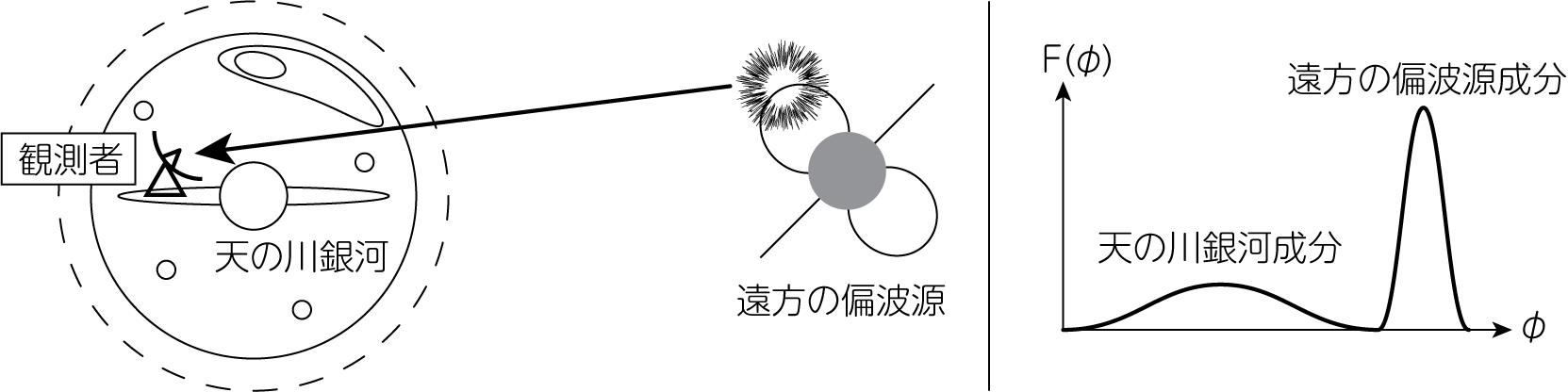
\(\lambda^2 < 0\)のとき、すなわち波長が複素数であるような場合には\(P(\lambda^2)\)は物理的な意味を持ちません。 よって\(P(\lambda^2)\)は\(\lambda^2 \geq 0\)の場合のみ、意味を持つ物理量です。 当然ながら\(\lambda^2 < 0\)での\(P(\lambda^2)\)は観測ができないため、\(\lambda^2 \geq 0\)における\(P(\lambda^2)\)の値から何かしらの仮定を置いて予測することで、始めて(4)式の逆変換を考えることができます。 用いられる仮定の例として\(P\)がエルミート、すなわち\(P = P^\dagger\)などがあります。 この仮定は\(F(\phi)\)が実数であることに対応します。
観測による制限: 窓関数の導入による一般化
(4)式の\(P(\lambda^2)\)は、実際には観測波長域によって制限されます。 そこで
\[\widetilde{P}(\lambda^2) = W(\lambda^2) P(\lambda^2) \tag{5}\]のような窓関数(あるいはサンプリング関数とも呼ばれる)\(W(\lambda^2)\)を導入しましょう。 これは観測する波長域では値をもち、それ以外ではゼロとなるような関数です。 以降、\(\widetilde{P}\)のようにチルダのついた物理量は、観測による制限を受けたものを意味します。 すると(4)式から
\[\widetilde{P}(\lambda^2) = W(\lambda^2) \int_{-\infty}^\infty F(\phi) e^{2i \phi \lambda^2} d\phi \tag{6}\]です。 以降の逆変換で係数\(1/\pi\)による煩雑化を避けるために、\(\lambda^2 = \pi u\)のように変数変換を施しましょう。 すると
\[\widetilde{P}(\pi u) = W(\pi u) \int_{-\infty}^\infty F(\phi) e^{2 \pi i \phi u} d\phi \tag{6}\]ここでさらに
\[R(\phi) \equiv \frac{\int_{-\infty}^\infty W(\pi u) e^{-2\pi i \phi u} du}{\int_{-\infty}^\infty W(\pi u) du} \tag{7}\]を定義しましょう。 これは窓関数\(W(\pi u)\)をフーリエ逆変換したものを、\(\phi = 0\)の値で規格化したものです。 (7)式の逆変換より
\[W(\pi u) = \left( \int_{-\infty}^\infty W(\pi u) du \right) \int_{-\infty}^\infty R(\phi) e^{2\pi i \phi u} d\phi \tag{8}\]です。 これと(6)式より
\[\widetilde{P}(\pi u) = \left( \int_{-\infty}^\infty W(\pi u') du' \right) \left( \int_{-\infty}^\infty R(\phi') e^{2\pi i \phi' u} d\phi' \right) \left( \int_{-\infty}^\infty F(\phi'') e^{2\pi i \phi'' u} d\phi'' \right) \tag{9}\]を得ます。 さらに逆変換を考えれば
\[\begin{align} \frac{\int_{-\infty}^\infty \widetilde{P}(\pi u) e^{-2\pi i \phi u} du}{\int_{-\infty}^\infty W(\pi u') du'} &= \int_{-\infty}^\infty \left( \int_{-\infty}^\infty R(\phi') e^{2\pi i \phi' u} d\phi' \right) \left( \int_{-\infty}^\infty F(\phi'') e^{2\pi i \phi'' u} d\phi'' \right) e^{-2\pi i \phi u} du \notag \\ &= \int_{-\infty}^\infty R(\phi') \left( \int_{-\infty}^\infty F(\phi'') \left( \int_{-\infty}^\infty e^{2\pi i(\phi'+\phi''-\phi) u} du \right) d\phi'' \right) d\phi' \notag \\ &= \int_{-\infty}^\infty R(\phi') \left( \int_{-\infty}^\infty F(\phi'') \delta(\phi'+\phi''-\phi) d\phi'' \right) d\phi' \notag \\ &= \int_{-\infty}^\infty R(\phi') F(\phi - \phi') d\phi' = R(\phi) \ast F(\phi) \tag{10} \end{align}\]のようになります。 最後の\(\ast\)は畳み込みを表すものです。 そして\(u = \lambda^2 / \pi\)として元に戻せば
\[\widetilde{F}(\phi) = F(\phi) * R(\phi) = K \int_{-\infty}^\infty \widetilde{P}(\lambda^2) e^{-2\pi i \lambda^2} d\lambda^2 \quad \left( K = \left( \int_{-\infty}^\infty W(\lambda^2) d\lambda^2 \right)^{-1}\right) \tag{11}\]のように、窓関数を考慮した\(\widetilde{F}(\phi)\)が求まります。 ここで、この\(R(\phi)\)はRotation Measure Spread Function (RMSF: 回転量度の広がり関数)と呼ばれるものです。 窓関数\(W(\lambda^2)\)を適用した結果、\(R(\phi)\)により元々のファラデースペクトル\(F(\phi)\)が修正を受けます。 このことから\(\widetilde{F}(\phi)\)のことを、”dirty Faraday spectrum” (汚染されたファラデースペクトル)と呼ぶこともあります。
観測から\(P(\lambda^2)\)を様々な波長域で観測し、その逆変換を行うことで、\(F(\phi)\)を求めることができます。
RM synthesisの欠点
例えば矩形の窓関数について考えましょう。 これをフーリエ変換すると、sinc関数になることが知られています。 この簡単な例からもわかるように、窓関数を通して得られた\(\widetilde{F}(\phi)\)は、元々の\(F(\phi)\)に比べて広がり(サイドローブ)を持つようになります。
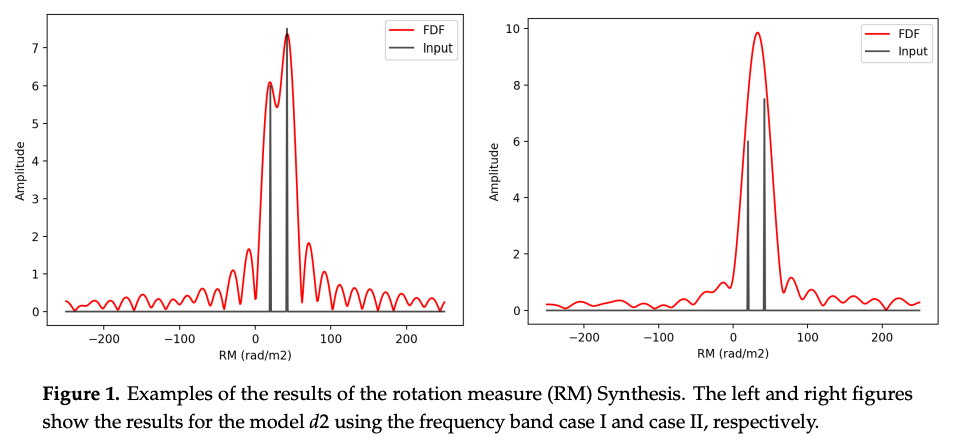
このサイドローブを除去し、真の\(F(\phi)\)に近いものを得る手法も開発されています。 良く知られている手法としてはRM CLEANと呼ばれるものがあります。
QU-fitting
先程は観測された\(P(\lambda^2)\)から\(F(\phi)\)を求めましたが、もう一つの求め方として、まず\(F(\phi)\)をモデルとして仮定します。 このモデルから(4)式を通して\(P(\lambda^2)\)を計算し、実際の観測量\(P(\lambda^2) = Q(\lambda^2) + i U(\lambda^2)\)とフィッティングを行います。 このようにして、観測を再現する\(F(\phi)\)を求める方法を、QU-fittingと呼びます。 モデルパラメータのフィッティングにはマルコフ連鎖モンテカルロ法(MCMC)などの統計技術が用いられます。
RM synthesis + RM CLEAN と QU-fittingの2つの手法を比較した表を、下に示します。
| RM Synthesis + RM CLEAN | QU-fitting | |
|---|---|---|
| モデルの仮定 | \(\bigcirc\) 陽には必要としない | \(\times\) 必要 |
| \(F(\phi)\)の推定 | \(\triangle\) 普通に計算できる | \(\bigcirc\)(もし適切なモデルが与えられれば)良い計算ができる |
| 誤差の推定 | \(\times\) できない | \(\bigcirc\) できる |
| 計算コスト | \(\bigcirc\) 低い | \(\times\) 高い |
\(\bigcirc, \triangle, \times\)はそれぞれ、良い・普通・悪いを表す記号です。 QU-fittingにはMCMCを用いるなどして計算コストを削減することが試みられていますが、それでもまだ計算量が高価なものと考えられています。
\(F(\phi) \rightarrow F(x)\)への変換
ここまで、ファラデー深度\(\phi\)における複素偏光強度分布\(F(\phi)\)を求める手法を紹介してきました。 このようにして得られた結果から、観測者からの距離\(x\)に位置する場所での複素偏光強度分布、すなわち\(F(x)\)を求めることができれば、そこからさらに視線方向の磁場や電子数密度の情報を引き出すことができます。 しかしこれまで考えてきたファラデー深度\(\phi\)と観測者からの距離\(x\)は一対一対応になっていません。
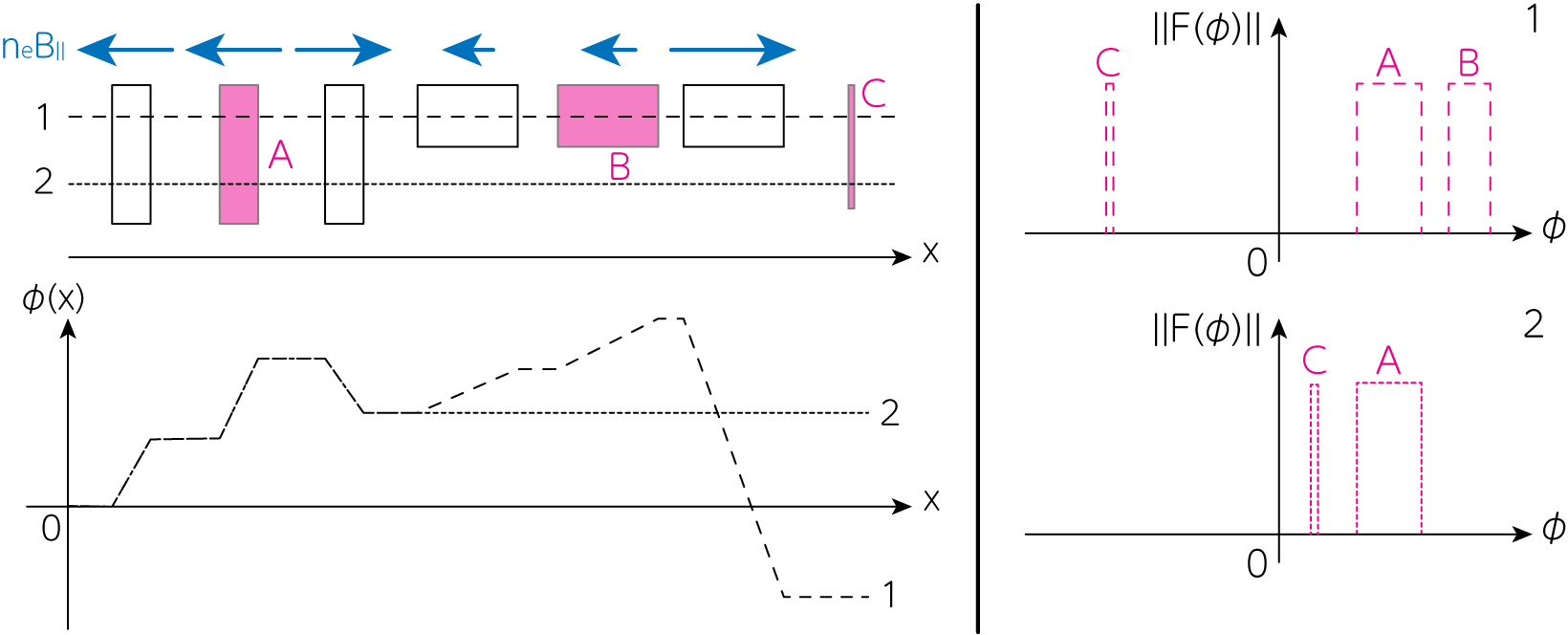
上左図は、横軸を観測者からの距離\(x\)としたときに、どのように\(\phi(x)\)が推移するかを表現したものです。 左上パネルには観測者の視線方向1, 2が描かれており、その視線方向に磁場を伴うプラズマ領域がいくつか存在します。 そして一番上の矢印が\(n_e B_\parallel\)を表しています。 視線方向1, 2では見ている領域が異なるために、\(\phi(x)\)のグラフに違いが現れています。 また薄く色付けされた領域A, Bは放射を出しながらも、ファラデー回転を伴う領域です。 さらに領域Cは放射のみを出し、ファラデー回転は伴わないような狭い領域を指します。 これらの領域の放射から\(F(\phi)\)を計算し、これを横軸\(\phi\)のグラフとして描くと右図のようになります。 右図上パネルが視線方向1, そして下パネルが視線方向2の\(F(\phi)\)を表したものです。 特に、同じ領域Cから来る放射でも\(F(\phi)\)の位置が変化していることがわかります。
ではファラデースペクトル\(F(\phi)\)は物理的な情報を持たないのでしょうか。 上図を見ればわかるように、例えば星間乱流のモデルを変えると、磁場の向きなども変化するため、\(F(\phi)\)の形状も変化します。 このことから\(F(\phi)\)は物理的な情報を含んではいるのですが、それを正しく引き出す研究は、今も精力的に行われています。
参考文献
[1] Brentjens & de Bruyn, 2005, “Faraday rotation measure synthesis”
[2] Ideguchi et al., 2018, “Faraday Tomography Tutorial”
[3] Ideguchi et al., 2014, “Faraday Dispersion Functions of Galaxies”
[4] Heald et al., “The Westerbork SINGS Survey II. Polarization, Faraday Rotation, and Magnetic Fields”
[5] Heald, “RM Synthesis”
[6] RM-Tools
[7] 出口真輔, “ファラデートモグラフィー:広帯域電波観測による新たな宇宙磁場観測法”
[8] 出口真輔, “ファラデートモグラフィー:広帯域偏波観測による新たな宇宙磁場探査法”
[9] 中川晶太, “宇宙磁場解析における QU-fitting”