連星系の重力場
以下の問題は、2022年に行われた東京大学大学院理学系研究科天文学専攻の大学院入試問題です。 連星系の重力場についての問題で、その時間変動などを求めるものになっています。 2017年にはノーベル物理学賞にも選ばれた重力波観測、その発生源となっている連星の重力に関する問題です。 一般相対論は用いず、古典力学の範疇で重力場の時間変化を計算します。 ぜひチャレンジしてみましょう。
問題
図1に示すように、距離\(\ell\)だけ離れた質量\(M/2\)の質点とみなせる2つの天体が、重力で引き合い重心の周りを角速度\(\omega\)で回転している系を考えましょう。 天体の回転面を\(x-y\)面、その垂直方向を\(z\)軸となるように座標設定をします。 この系の重心\(O\)から距離\(r \ (>0)\)だけ離れた点を\(P\)とし、\(OP\)が\(z\)軸となす角度を\(\theta\)、\(OP\)の\(x-y\)面への射影が\(x\)軸となす角度を\(\varphi\)とします。 このとき、以下の設問に答えなさい。 なお、本設問では\(G\)を重力定数、\(t\)を時刻とします。 また\(t=0\)のとき、天体1は\(+x\)軸上にあるとします。
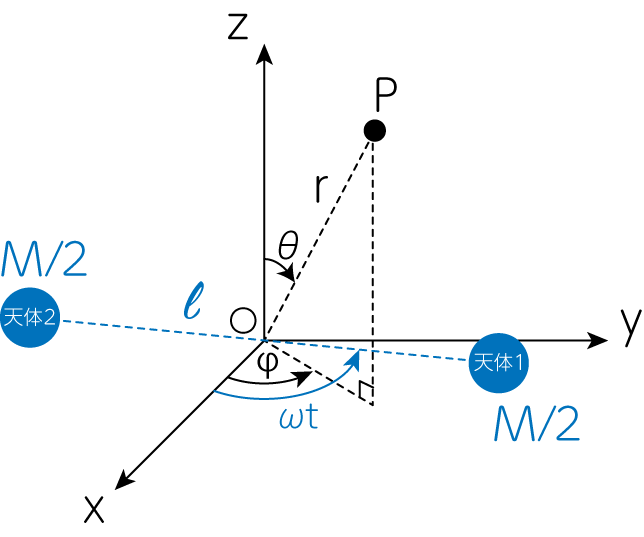
問1
天体1の中心から\(P\)点に伸びるベクトルと\(\mathbf{r}_1\)とするとき、\(\mathbf{r}_1\)の\(x, y, z\)成分を求めなさい。
問2
地点\(P\)に質量\(m\)の質点を置いたとき、天体1, 2が作るこの質点の重力ポテンシャル\(U(r)\)が
\[U(r) = -\frac{GmM}{2r} \left[ \frac{1}{\sqrt{1+\left(\frac{\ell}{2r}\right)^2 -\frac{\ell}{r} \sin \theta \cos (\varphi - \omega t)}} + \frac{1}{\sqrt{1+\left(\frac{\ell}{2r}\right)^2 + \frac{\ell}{r} \sin \theta \cos (\varphi - \omega t)}}\right] \tag{1}\]となることを示しなさい。
問3
\(OP\)間の距離\(r\)が天体間の距離\(\ell\)よりも十分に大きい場合\((r \gg \ell)\)を考えましょう。
(a)
(1)式の重力ポテンシャル\(U(r)\)を\(\frac{\ell}{2r}\)についてテイラー展開し、0, 1, 2次項を求めなさい。
(b)
(a)で求めた0, 1, 2次項がどのような物理的意味を持っているのか、簡潔な文章で説明しなさい。
(c)
(a)を用いてこの質量\(m\)の質点が受ける重力の大きさの近似値を求めなさい。
(d)
(c)で求めた重力の大きさから、時間変動成分の周波数と振幅を求めなさい。
解答例
問1
原点\(O\)から\(P\)に向かう位置ベクトルは
\[\mathbf{r} = r \left( \begin{array}{c} \sin \theta \cos \varphi \\ \sin \theta \sin \varphi \\ \cos \theta \end{array} \right) \tag{1-1}\]のように表記されます。 一方、連星を成している天体1の位置ベクトルを\(\mathbf{R}_1\)とすると、これは
\[\mathbf{R}_1 = \frac{\ell}{2} \left( \begin{array}{c} \cos \omega t \\ \sin \omega t \\ 0 \end{array} \right) \tag{1-2}\]と書かれます。 これらより
\[\mathbf{r}_1 = \mathbf{r} - \mathbf{R}_1 = \left( \begin{array}{c} r \sin \theta \cos \varphi - \frac{\ell}{2} \cos \omega t \\ r \sin \theta \sin \varphi - \frac{\ell}{2} \sin \omega t \\ r \cos \theta \end{array} \right) \tag{1-3}\]のように計算されます。
問2
天体1, 2が作る重力ポテンシャルをそれぞれ\(U_1(\mathbf{r}), U_2(\mathbf{r})\)とすると
\[U_1(\mathbf{r}) = - \frac{GMm}{2r_1}, \quad U_2(\mathbf{r}) = - \frac{GMm}{2r_2} \tag{2-1}\]です。 ここで\(r_2\)は、天体2から点\(P\)までの距離です。 (1-3)式より
\[\begin{align} r_1^2 &= \left(r \sin \theta \cos \varphi - \frac{\ell}{2} \cos \omega t \right)^2 + \left(r \sin \theta \sin \varphi - \frac{\ell}{2} \sin \omega t\right)^2 + r^2 \cos^2 \theta \notag \\ &= r^2 - r\ell \sin \theta (\cos \varphi \cos \omega t + \sin \varphi \sin \omega t) + \left(\frac{\ell}{2}\right)^2 = r^2 \left\{ 1 - 2 \frac{\ell}{2r} \sin \theta \cos (\varphi - \omega t) + \left(\frac{\ell}{2r}\right)^2 \right\} \tag{2-2} \end{align}\]のように計算されます。 同様に\(\mathbf{r}_2\)を求め、その大きさ\(r_2\)を求めると
\[r_2^2 = r^2 \left\{ 1 + 2 \frac{\ell}{2r} \sin \theta \cos (\varphi - \omega t) + \left(\frac{\ell}{2r}\right)^2 \right\} \tag{2-3}\]となります。 以上より、求める重力ポテンシャルは
\[U (\mathbf{r}) = U_1 (\mathbf{r}) + U_2 (\mathbf{r}) = - \frac{GMm}{2r} \left\{ \frac{1}{\sqrt{1 - 2\frac{\ell}{2r} \sin \theta \cos (\varphi - \omega t)} + \left( \frac{\ell}{2r}\right)^2} + \frac{1}{\sqrt{1 + 2\frac{\ell}{2r} \sin \theta \cos (\varphi - \omega t)} + \left( \frac{\ell}{2r}\right)^2}\right\} \tag{2-4}\]と求まります。
問3
(a)
普通にテイラー展開を行っても良いですが、せっかくなのでルジャンドル多項式を用いて表現してみましょう。 ルジャンドル多項式 \(P_n\)は母関数を用いて
\[\frac{1}{\sqrt{1-2zw + w^2}} = \sum_{n=0}^\infty P_n(z) w^n \tag{3-a-1}\]のように表されます。 \(z = \sin \theta \cos (\varphi - \omega t), w = \frac{\ell}{2r}\)として
\[\frac{1}{\sqrt{1 - 2\frac{\ell}{2r} \sin \theta \cos (\varphi - \omega t)} + \left( \frac{\ell}{2r}\right)^2} = \sum_{n=0}^\infty P_n (\sin \theta \cos (\varphi - \omega t)) \left( \frac{\ell}{2r}\right)^n \tag{3-a-2}\]上式で\(z = - \sin \theta \cos (\varphi - \omega t)\)とすれば
\[\frac{1}{\sqrt{1 + 2\frac{\ell}{2r} \sin \theta \cos (\varphi - \omega t)} + \left( \frac{\ell}{2r}\right)^2} = \sum_{n=0}^\infty P_n (-\sin \theta \cos (\varphi - \omega t)) \left( \frac{\ell}{2r}\right)^n \tag{3-a-3}\]を得ます。 ルジャンドル多項式の性質\(P_n (-z) = (-1)^n P_n(z)\)より
\[U(\mathbf{r}) = -\frac{GMm}{2r} \sum_{n=0}^\infty \left\{ 1 + (-1)^n \right\} P_n (\sin \theta \cos (\varphi - \omega t)) \left( \frac{\ell}{2r} \right)^n \tag{3-a-4}\]のように求まります。 0次、1次、2次の項をそれぞれ\(U_0, U_1, U_2\)のように表記しましょう。 すると\(P_0(z) = 1, P_1(z) = z, P_2(z) = \frac{1}{2} (3z^2 - 1)\)より
\[U_0 (\mathbf{r}) = - \frac{GMm}{r}, \quad U_1 (\mathbf{r}) = 0, \quad U_2 = - \frac{GMm}{2r} \left\{ 3\sin^2 \theta \cos^2 (\varphi - \omega t) - 1 \right\} \left( \frac{\ell}{2r}\right)^2 \tag{3-a-5}\]となります。
(b)
0次の項は、連星系を成している2つの天体の質量の合計\(M\)が原点に存在する場合の重力ポテンシャルと同じ形をしています。 このことからもわかるように、これはこの系を単極子近似した場合の重力ポテンシャルです。
1次の項はゼロになっていますが、これはこの連星系の重力場を双極子として近似した場合に対応します。 電磁気学ではプラスの電荷とマイナスの電荷が存在することから、双極子成分が存在します。 しかし、重力相互作用においてはマイナスの質量が存在しないため、双極子成分はゼロとなります。
2次の項は4重極成分を表します。 簡単のため、(3-a-5)式において\(\theta = \pi/2\)、すなわち\(xy\)平面上で考えることにしましょう。 すると\(\cos^2 (\varphi - \omega t)\)の部分からわかるように、\(U_2\)は方位角\(\varphi\)に対して周期\(\pi/2\)の関数となっていることがわかります。 このことから、\(0 \leq \varphi \leq 2\pi\)の間に4つのポテンシャルの極大が存在することから、これは4重極成分を表すことがわかります。
(c)
重力は\(\mathbf{F} = - \nabla U\)のように計算されます。 (3-a-5)式のように重力ポテンシャルが3次元極座標で表現されているため、この勾配計算は極座標で行うと良いでしょう。 重力ポテンシャルの0, 1, 2次の項からくる重力をそれぞれ\(\mathbf{F}_0, \mathbf{F}_1, \mathbf{F}_2\)のように書く
\[\mathbf{F}_0 = - \nabla U_0 = \frac{\partial}{\partial r} \frac{GMm}{r} \mathbf{e}_r = - \frac{GMm}{r^2} \mathbf{e}_r \tag{3-c-1}\] \[\mathbf{F}_1 = \mathbf{0} \tag{3-c-2}\] \[\begin{align} \mathbf{F}_2 &= - \nabla U_2 = \frac{GMm \ell^2}{8} \nabla \left[ \frac{3 \sin^2 \theta \cos^2 (\varphi - \omega t) -1}{r^3}\right] \notag \\ &= \frac{GMm}{2r^2} \left(\frac{\ell}{2r}\right)^2 [ (-3) \{ 3\sin^2 \theta \cos^2 (\varphi - \omega t) -1 \} \mathbf{e}_r \notag \\ & \qquad \qquad \qquad + 6 \sin \theta \cos \theta \cos^2 (\varphi - \omega t) \mathbf{e}_\theta -6 \sin \theta \cos (\varphi - \omega t ) \sin (\varphi - \omega t) \mathbf{e}_\varphi ] \tag{3-c-3} \end{align}\]これらを用いて重力の大きさを計算しましょう。
\[F = \vert \mathbf{F}_0 + \mathbf{F}_2 \vert = \sqrt{F_0^2 + F_2^2 + 2 \mathbf{F}_0 \cdot \mathbf{F}_2} \tag{3-c-4}\]ですが、(3-c-3)式より、\(\mathbf{F}_2\)はすでに\(\left( \frac{\ell}{2r}\right)^2\)のオーダーです。 よって\(F_2^2\)は微小量として無視すると
\[\begin{align} F &\approx \sqrt{\left( \frac{GMm}{r^2}\right)^2 + \left( \frac{GMm}{r^2}\right)^2 \left( \frac{\ell}{2r}\right)^2 3 \{ 3\sin^2 \theta \cos^2 (\varphi - \omega t) -1 \}} \notag \\ &= \frac{GMm}{r^2} \sqrt{ 1 + \left( \frac{\ell}{2r}\right)^2 3 \{ 3\sin^2 \theta \cos^2 (\varphi - \omega t) -1 \}} \notag \end{align}\]のようになります。 さらに\(\sqrt{1+Cx} \approx 1 + \frac{C}{2} x\)のように近似を行えば
\[F \approx \frac{GMm}{r^2} \left[ 1 + \left( \frac{\ell}{2r}\right)^2 \frac{3}{2} \{ 3\sin^2 \theta \cos^2 (\varphi - \omega t) -1 \}\right] \tag{3-c-5}\]を得ます。 さらに\(\cos^2 \alpha = \frac{1 + 2\cos \alpha}{2}\)から、時間変動部分は
\[振幅: \frac{9GMm}{4r^2} \left( \frac{\ell}{2r}\right)^2 \sin^2 \theta, \quad 周波数: 2\omega \tag{3-c-6}\]のようになります。 重力の時間変動振幅は\(\left(\frac{\ell}{2r}\right)^2\)からわかるように非常に小さいことがわかります。
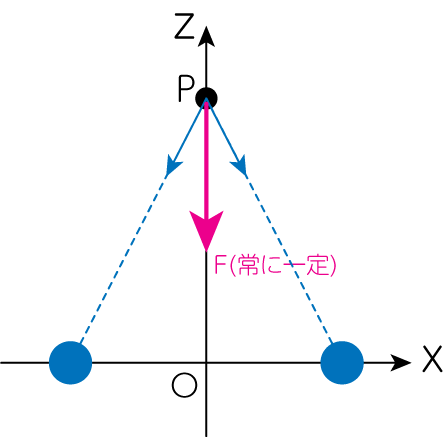
また周波数が\(2\omega\)となるのは、4重極であることからくるものです。 一般相対論から導き出される重力波の振動数も、連星などの回転体の周波数の2倍となることが知られています。 振幅に\(\sin^2 \theta\)が入っていることからもわかるように、\(\theta = 0, \pi\)では時間変動の振幅はゼロ、すなわち連星からの重力の変化を感じられないことがわかります。 これは下図のように\(z\)軸上に点\(P\)がある場合、連星からの重力の大きさが一定となるためです。 このことは(3-c-3)式に\(\theta =0, \pi\)を代入しても確かめることができます。
参考文献
[1] 東京大学大学院理学系研究科天文学専攻、令和5年度修士・博士課程入学試験問題
[2] 安東正樹, 重力波天文学入門