Table of contents
レイリー・テイラー不安定性とケルビン・ヘルムホルツ不安定性
ここでは様々なところで見られるレイリー・テイラー不安定性(Rayleigh-Taylor Instability; RTI)とケルビン・ヘルムホルツ不安定性(Kelvin-Helmholtz Instability; KHI)についてメモします。 ただし、以下では一様磁場が存在する磁気流体中での不安定性を考えていきます。
レイリー・テイラー不安定性の直感的理解
まずは座標設定からです。下図のように\(y=0\)を境界面として、2つの密度や速度が異なる媒質が層をなしているとします。\(y\)が負の方向に一様重力も存在しているとします。 今、この境界面に微小な摂動が加わり、境界面が図の点線のように変化したとします。

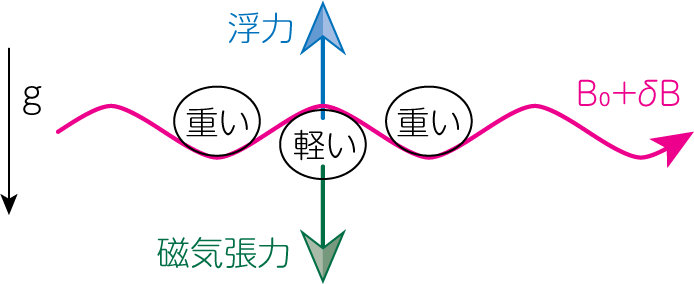
上図に置いて\(\rho_0^{(1)}>\rho_0^{(2)}\)のように、単位体積あたりの質量が重たい流体が軽い流体の上に乗っかっている場合を考えます。ここに摂動が加わると、下から持ち上がった部分は周囲よりも軽いために浮力を感じ、より上昇しようとします。 逆に、上から下に突き出た部分は周囲よりも重たいため、重力でさらに下降します。このようにして、上に乗っていた重たい流体と下の軽い流体の混合が起こります。ただし磁場が存在する場合には、磁力線による磁気張力が存在するため、浮力による上昇や重力による下降が妨げられます。 これが磁場がある場合のレイリー・テイラー不安定性の直感的な理解です。
ケルビン・ヘルムホルツ不安定性の直感的理解
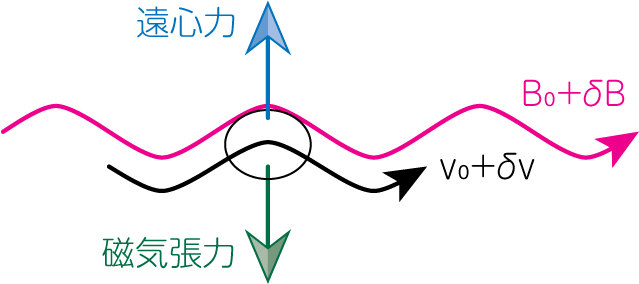
先程と同じ座標設定ですが、今度は速度シアがある場合、すなわち\(v_0^{(1)} \neq v_0^{(2)}\)のような場合を考えましょう。ここからさらにガリレイ変換を行い、どちらかの速度のみが観測されるような系に移ります。 摂動が加わることで、下図のように境界面に沿って流線も変化します。すると流体要素の軌道が曲げられることで、流体要素は遠心力を感じるようになります。これにより上に凸の部分には上向きの力、下に凸の部分には下向きの力が生じ、2流体の混合が起こります。 この場合も、磁場が存在する場合には、磁力線による磁気張力がこの運動を妨げます。これが磁場がある場合のケルビン・ヘルムホルツ不安定性の直感的な理解です。
基礎方程式
それでは、この2つの不安定性を定量的に評価していきましょう。簡単のため、以下では非圧縮を仮定します。
\[\nabla \cdot \mathbf{v} = 0 \tag{1}\]連続の式より
\[\frac{\partial \rho}{\partial t} + \nabla \cdot (\rho \mathbf{v}) = 0 \tag{2}\]運動量保存の式より
\[\frac{\partial}{\partial t} (\rho \mathbf{v}) + \nabla \cdot \left\{ \rho \mathbf{v}\mathbf{v} - \frac{1}{4\pi} \mathbf{B}\mathbf{B} + \left( P + \frac{1}{8\pi} B^2\right) \mathbf{I} \right\} = - \rho g \mathbf{e}_y \tag{3}\]誘導方程式より
\[\frac{\partial \mathbf{B}}{\partial t} = \nabla \times (\mathbf{v} \times \mathbf{B}) \tag{4}\]マクスウェル方程式から、磁気単極子が存在しないことを表す式より
\[\nabla \cdot \mathbf{B} = 0 \tag{5}\]方程式の線形化
最初、系は定常状態にあるとします。そのときの物理量をそれぞれ
\[\rho = \rho_0, \quad \mathbf{v} = \mathbf{v}_0 = (v_0, 0, 0), \quad \mathbf{B} = \mathbf{B}_0 = (B_0, 0, 0), P = P_0\]とします。\(\rho_0, v_0, P_0\)は\(y\)のみの関数で、\(B_0\)は定数であるとします。(1)-(5)式より
\[\nabla \cdot \mathbf{v}_0 = 0 \tag{6}\] \[\nabla \cdot (\rho_0 \mathbf{v}_0) = 0 \tag{7}\] \[\nabla \cdot \left\{ \rho_0 \mathbf{v}_0 \mathbf{v}_0 - \frac{1}{4\pi} \mathbf{B}_0 \mathbf{B}_0 + \left( P_0 + \frac{1}{8\pi} B_0^2 \right) \mathbf{I}\right\} = - \rho_0 g \mathbf{e}_y \tag{8}\] \[\nabla \times (\mathbf{v}_0 \times \mathbf{B}_0) = \mathbf{0} \tag{9}\] \[\nabla \cdot \mathbf{B}_0 = 0 \tag{10}\]ここに微小な摂動が加わり、物理量がそれぞれ
\[\rho = \rho_0 + \delta \rho, \quad \mathbf{v} = \mathbf{v}_0 + \delta \mathbf{v} = (v_0 + \delta v_x, \delta v_y, 0), \quad \mathbf{B} = \mathbf{B}_0 + \delta \mathbf{B} = (B_0 + \delta B_x, \delta B_y, 0), \quad P = P_0 + \delta P\]のように変化したとします。これらを(1)-(5)式に代入していきましょう。(1)式より
\[\underbrace{\nabla \cdot \mathbf{v}_0}_{(6)} + \nabla \cdot \delta \mathbf{v} = \nabla \cdot \delta \mathbf{v} = 0 \tag{11}\]次に(2)式からは
\[\begin{align} &\frac{\partial}{\partial t} (\rho_0 + \delta \rho) + \nabla \cdot \left\{ (\rho_0 + \delta \rho) (\mathbf{v}_0 + \delta \mathbf{v})\right\} = \frac{\partial \delta \rho}{\partial t} + \underbrace{\nabla \cdot (\rho_0 \mathbf{v}_0)}_{(7)} + \nabla \cdot (\delta \rho \mathbf{v}_0 + \rho_0 \delta \mathbf{v}) \notag \\ &= \frac{\partial \delta \rho}{\partial t} + (\mathbf{v}_0 \cdot \nabla) \delta \rho + \delta \rho \underbrace{(\nabla \cdot \mathbf{v}_0)}_{(6)} + (\delta \mathbf{v} \cdot \nabla) \rho_0 + \rho_0 \underbrace{(\nabla \cdot \delta \mathbf{v})}_{(11)} \notag \\ &= \frac{\partial \delta \rho}{\partial t} + (\mathbf{v}_0 \cdot \nabla) \delta \rho + (\delta \mathbf{v} \cdot \nabla) \rho_0 = 0 \tag{12} \end{align}\]続いて(3)式です。
\[\begin{align} &\frac{\partial }{\partial t} \left\{ (\rho_0 + \delta \rho) (\mathbf{v}_0 + \delta \mathbf{v}) \right\} \notag \\ &\qquad + \nabla \cdot \left\{ (\rho_0 + \delta \rho) (\mathbf{v}_0 + \delta \mathbf{v}) (\mathbf{v}_0 + \delta \mathbf{v}) - \frac{1}{4\pi} (\mathbf{B} + \delta \mathbf{B}) (\mathbf{B}_0 + \delta \mathbf{B}) + \left( P_0 + \delta P + \frac{1}{8\pi} (\mathbf{B}_0 + \delta \mathbf{B}) \cdot (\mathbf{B}_0 + \delta \mathbf{B})\right) \mathbf{I}\right\} \notag \\ &= \frac{\partial }{\partial t} (\rho_0 \delta \mathbf{v} + \delta \rho \mathbf{v}_0) + \nabla \cdot \left\{ \rho_0 \mathbf{v}_0 \mathbf{v}_0 + \delta \rho \mathbf{v}_0 \mathbf{v}_0 + \rho_0 \mathbf{v}_0 \delta \mathbf{v} \right. \notag \\ &\qquad \left. + \rho_0 \delta \mathbf{v} \mathbf{v}_0 - \frac{1}{4\pi} (\mathbf{B}_0 \mathbf{B}_0 + \mathbf{B}_0 \delta \mathbf{B} + \delta \mathbf{B} \mathbf{B}_0) + \left( P_0 + \delta P + \frac{1}{8\pi} (B_0^2 + 2 \delta \mathbf{B} \cdot \mathbf{B}_0)\right) \mathbf{I}\right\} \notag \\ &= - (\rho_0 + \delta \rho) g \mathbf{e}_y \notag \end{align}\]ここで(8)式を用いると
\[\begin{align} &\frac{\partial }{\partial t} (\rho_0 \delta \mathbf{v} + \delta \rho \mathbf{v}_0) + \nabla \cdot \left\{ \delta \rho \mathbf{v}_0 \mathbf{v}_0 + \rho \mathbf{v}_0 \delta \mathbf{v} + \rho_0 \delta \mathbf{v} \mathbf{v}_0 - \frac{1}{4\pi} (\mathbf{B}_0 \delta \mathbf{B} + \delta \mathbf{B} \mathbf{B}_0) + \left(\delta P + \frac{1}{4\pi} \delta \mathbf{B} \cdot \mathbf{B}_0\right) \mathbf{I}\right\} \notag \\ &= - \delta \rho g \mathbf{e}_y \tag{13} \end{align}\]さらに(4)式は
\[\begin{align} \frac{\partial }{\partial t} (\mathbf{B}_0 + \delta \mathbf{B}) - \nabla \times \{ (\mathbf{v}_0 + \delta \mathbf{v}) \times (\mathbf{B}_0 + \delta \mathbf{B})\} &= \frac{\partial \delta \mathbf{B}}{\partial t} - \nabla \times (\mathbf{v}_0 \times \mathbf{B}_0 + \mathbf{v}_0 \times \delta \mathbf{B} + \delta \mathbf{v} \times \mathbf{B}_0) \notag \\ &\underbrace{=}_{(9)} \frac{\partial \delta \mathbf{B}}{\partial t} - \nabla \times (\mathbf{v}_0 \times \delta \mathbf{B} + \delta \mathbf{v} \times \mathbf{B}_0) \notag \\ &= \mathbf{0} \tag{14} \end{align}\]最後に(5)式は
\[\nabla \cdot (\mathbf{B}_0 + \delta \mathbf{B}) \underbrace{=}_{(10)} \nabla \cdot \delta \mathbf{B} = 0 \tag{15}\]のようになります。ここまではベクトルの形を保持したまま式変形しましたが、ここからは具体的に成分をあらわにして式変形しましょう。(11)式より
\[\frac{\partial \delta v_x}{\partial x} + \frac{\partial \delta v_y}{\partial y} = 0 \tag{16}\](12)式より
\[\frac{\partial \delta \rho}{\partial t} + v_0 \frac{\partial \delta \rho}{\partial x} + \delta v_x \underbrace{\frac{\partial \rho_0}{\partial x}}_{=0} + \delta v_y \frac{\partial \rho_0}{\partial y} = \frac{\partial \delta \rho}{\partial t} + v_0 \frac{\partial \delta \rho}{\partial x} + \delta v_y \frac{\partial \rho_0}{\partial y} = 0 \tag{17}\](15)式より
\[\frac{\partial \delta B_x}{\partial x} + \frac{\partial \delta B_y}{\partial y} = 0 \tag{18}\](13)式の\(x\)成分より
\[\begin{align} &\rho_0 \frac{\partial \delta v_x}{\partial t} + \underbrace{v_0 \frac{\partial \delta \rho}{\partial t}}_{(17)} + \frac{\partial}{\partial x} \left\{ (\delta \rho v_0) v_0 + (\rho_0 v_0) \delta v_x + (\rho_0 \delta v_x) v_0 - \frac{1}{4\pi} B_{0x} \delta B_x - \frac{1}{4\pi} \delta B_x B_0 + \delta P + \frac{1}{4\pi} \delta B_x B_0\right\} \notag \\ & \qquad + \frac{\partial}{\partial y} \left\{ (\rho_0 v_0) \delta v_y - \frac{1}{4\pi} B_0 \delta B_y \right\} = 0 \notag \\ &\Longrightarrow \ \rho_0 \frac{\partial \delta v_x}{\partial t} - v_0 \left( v_0 \frac{\partial \delta \rho}{\partial x} - \delta v_y \frac{\partial \rho_0}{\partial y}\right) + \frac{\partial}{\partial x} \left( v_0^2 \delta \rho + 2 \rho_0 v_0 \delta v_x - \frac{1}{4\pi} B_0 \delta B_x + \delta P\right) + \frac{\partial}{\partial y} \left( \rho_0 v_0 \delta v_y - \frac{1}{4\pi} B_0 \delta B_y\right) = 0 \notag \\ &\Longrightarrow \ \rho_0 \frac{\partial \delta v_x}{\partial t} + 2 \rho_0 v_0 \frac{\partial \delta v_x}{\partial x} - \frac{1}{4\pi} B_0 \frac{\partial \delta B_x}{\partial x} + \frac{\partial \delta P}{\partial x} + \rho_0 \delta v_y \frac{\partial v_0}{\partial y} + \rho_0 v_0 \frac{\partial \delta v_y}{\partial y} - \frac{1}{4\pi} B_0 \frac{\partial \delta B_y}{\partial y} \notag \\ & \qquad \qquad \qquad = \rho_0 \frac{\partial \delta v_x}{\partial t} + \rho_0 v_0 \frac{\partial \delta v_x}{\partial x} + \rho_0 v_0 \underbrace{\left( \frac{\partial \delta v_x}{\partial x} + \frac{\partial \delta v_y}{\partial y}\right)}_{(16)} - \frac{1}{4\pi} B_0 \underbrace{\left( \frac{\partial \delta B_x}{\partial x} + \frac{\partial \delta B_y}{\partial y}\right)}_{(18)} + \frac{\partial \delta P}{\partial x} + \rho_0 \delta v_y \frac{\partial v_0}{\partial y} = 0 \notag \end{align}\]以上から
\[\rho_0 \frac{\partial \delta v_x}{\partial t} + \rho_0 v_0 \frac{\partial \delta v_x}{\partial x} + \frac{\partial \delta P}{\partial x} + \rho_0 \delta v_y \frac{\partial v_0}{\partial y} = 0 \tag{19}\]を得ます。同様に、(13)式の\(y\)成分より
\[\rho_0 \frac{\partial \delta v_y}{\partial t} + \frac{\partial}{\partial x} \left( \rho_0 \delta v_y v_0 - \frac{1}{4\pi} \delta B_y B_0\right) + \frac{\partial}{\partial y} \left( \delta P + \frac{1}{4\pi} \delta B_x B_0 \right) = - \delta \rho g \tag{20}\]となります。さらに(14)式の\(x\)成分より
\[\begin{align} \frac{\partial \delta B_x}{\partial t} - \frac{\partial}{\partial y} (\mathbf{v}_0 \times \delta \mathbf{B} + \delta \mathbf{v} \times \mathbf{B}_0)_z &= \frac{\partial \delta B_x}{\partial t} - \frac{\partial}{\partial y} (v_0 \delta B_y - \delta v_y B_0) \notag \\ &= \frac{\partial \delta B_x}{\partial t} - \delta B_y \frac{\partial v_0}{\partial y} - v_0 \underbrace{\frac{\partial \delta B_y}{\partial y}}_{(16)} + B_0 \underbrace{\frac{\partial \delta v_y}{\partial y}}_{(16)} \notag \\ &= \frac{\partial \delta B_x}{\partial t} - \delta B_y \frac{\partial v_0}{\partial y} + v_0 \frac{\partial \delta B_x}{\partial x} + B_0 \frac{\partial \delta v_x}{\partial x} = 0 \tag{21} \end{align}\]最後に(14)式の\(y\)成分より
\[\frac{\partial \delta B_y}{\partial t} + \frac{\partial}{\partial x} (\mathbf{v}_0) \times \delta \mathbf{B} + \delta \mathbf{v} \times \mathbf{B}_0 ) = \frac{\partial \delta B_y}{\partial t} + \frac{\partial}{\partial x} (v_0 \delta B_y - \delta v_y B_0) = \frac{\partial \delta B_y}{\partial t} + v_0 \frac{\partial \delta B_y}{\partial x} - B_0 \frac{\partial \delta v_y}{\partial x} = 0 \tag{22}\]フーリエモード
ここで\(\rho, \mathbf{v}, \mathbf{B}, P\)の微小摂動の1つのフーリエモードに着目します。すなわち
\[\delta \rho, \delta \mathbf{v}, \delta \mathbf{B}, \delta P \propto e^{i(kx-\omega t)}\]とします。すると(16)式より
\[ik \delta v_x + \frac{\partial \delta v_y}{\partial y} \ \Longrightarrow \ \delta v_x = \frac{i}{k} \frac{\partial \delta v_y}{\partial y} \tag{23}\](17)式からは
\[- i \omega \delta \rho + \delta v_y \frac{\partial \rho_0}{\partial y} + ik v_0 \delta \rho = 0 \ \Longrightarrow \ \delta \rho = \frac{i}{k v_0 - \omega} \delta v_y \frac{\partial \rho_0}{\partial y} \tag{24}\](19)式は
\[\begin{align} &-i\omega \rho_0 \delta v_x + i k \rho_0 v_0 \delta v_x + i k \delta P + \rho_0 \delta v_y \frac{\partial v_0}{\partial y} = 0 \notag \\ &\Longrightarrow \ \delta P = \frac{\omega - k v_0}{k} \rho_0 \underbrace{\delta v_x}_{(23)} + i \frac{\rho_0}{k} \delta v_y \frac{\partial v_0}{\partial y} = i \frac{\omega - k v_0}{k^2} \rho_0 \frac{\partial \delta v_y}{\partial y} + i \frac{\rho_0}{k} \delta v_y \frac{\partial v_0}{\partial y} \tag{25} \end{align}\](20)式は
\[\begin{align} &- i \omega \rho_0 \delta v_y + i k \rho_0 v_0 \delta v_y - \frac{ik}{4\pi} B_0 \delta B_y + \frac{\partial}{\partial y} \underbrace{\delta P}_{(25)}+ \frac{1}{4\pi} B_0 \frac{\partial \delta B_x}{\partial y} = - \underbrace{\delta \rho}_{(24)} g \notag \\ &\Longrightarrow \ - i \rho_0(\omega - k v_0) \delta v_y - \frac{ik}{4\pi} B_0 \delta B_y + \frac{\partial}{\partial y} \left( i \frac{\omega - kv_0}{k^2} \rho_0 \frac{\partial \delta v_y}{\partial y} + i \frac{\rho_0}{k} \delta v_y \frac{\partial v_0}{\partial y}\right) + \frac{1}{4\pi} B_0 \frac{\partial \delta B_x}{\partial y} = \frac{ig}{\omega -kv_0} \delta v_y \frac{\partial \rho_0}{\partial y} \tag{26} \end{align}\](22)式からは
\[- i\omega \delta B_y + i k v_0 \delta B_y - ik B_0 \delta v_y = - i (\omega - kv_0) \delta B_y - ikB_0 \delta v_y \ \Longrightarrow \ \delta B_y = - \frac{k}{\omega-kv_0} B_0 \delta v_y \tag{27}\]そして(18)式から
\[ik \delta B_x + \frac{\partial \delta B_y}{\partial y} = 0 \ \Longrightarrow \ \delta B_x = \frac{i}{k} \frac{\partial}{\partial y} \underbrace{\delta B_y}_{(27)} = -i \frac{\partial}{\partial y} \left( \frac{B_0}{\omega-kv_0} \delta v_y\right) \tag{28}\](26)式に\(k^2 / i\)をかけ、(27), (28)式を代入すると
\[- \rho_0 k^2 (\omega -kv_0) \delta v_y + \frac{k^4}{\omega - kv_0} \frac{B_0^2}{4\pi} \delta v_y + \frac{\partial}{\partial y} \left\{ (\omega -kv_0) \rho_0 \frac{\partial \delta v_y}{\partial y} + k \rho_0 \delta v_y \frac{\partial v_0}{\partial y} \right\} - \frac{k^2 B_0^2}{4\pi} \frac{\partial^2}{\partial y^2} \left( \frac{\delta v_y}{\omega -kv_0}\right) = \frac{gk^2}{\omega-kv_0} \delta v_y \frac{\partial \rho_0}{\partial y}\]これを整理して
\[\frac{\partial}{\partial y} \left\{ (\omega -kv_0) \rho_0 \frac{\partial \delta v_y}{\partial y} + k \rho_0 \delta v_y \frac{\partial v_0}{\partial y} \right\} - \rho_0 k^2 (\omega -kv_0) \delta v_y = \frac{k^2 B_0^2}{4\pi} \left( \frac{\partial^2}{\partial y^2} - k^2\right) \left( \frac{\delta v_y}{\omega -kv_0}\right) + \frac{k^2g}{\omega-kv_0} \delta v_y \frac{\partial \rho_0}{\partial y} \tag{29}\]
境界面以外の取り扱い
今の場合、\(\)y \neq 0\(では\)\frac{\partial \rho_0}{\partial y} = \frac{\partial v_0}{\partial y} = 0$$より、(29)式は
\[\begin{align} &(\omega -kv_0) \rho_0 \frac{\partial^2 \delta v_y}{\partial y^2} - \rho_0 k^2 (\omega -kv_0) \delta v_y = \frac{k^2 B_0^2}{4\pi (\omega -kv_0)} \left( \frac{\partial^2}{\partial y^2} - k^2\right) \delta v_y \notag \\ &\Longrightarrow \ \left\{ (\omega-kv_0)^2 \rho_0 - \frac{k^2 B_0^2}{4\pi} \right\} \left( \frac{\partial^2}{\partial y^2} - k^2\right) \delta v_y = 0 \tag{30} \end{align}\]さらに、摂動は境界面に加えられていることを思い出すと、境界面から\(y\)方向に離れるにつれて摂動は小さくなると考えることができます。よって(29)式の解として
\[\delta v_y = A e^{-k |y|} \quad (A: 定数) \tag{31}\]のような形となるとわかります。次に2流体が接している境界面\(y=0\)について考えましょう。摂動が加わったことで境界面は変形します。その形を\(Y = \eta (x, t)\)のように表すと、この境界面は流体と共に運動し、それは波動のように\(x\)方向に伝播します。よってラグランジュ微分を用いて
\[\delta v_y = \frac{D\eta}{Dt} = \left\{ \frac{\partial}{\partial t} + (v_0 + \delta v_x) \frac{\partial}{\partial x} \right\} \eta\]境界面の変動\(\eta\)についても\(\eta \propto e^{i(kx-\omega t)}\)とし、さらに振幅も十分小さいとして線形化すると
\[\delta v_y = \{ -i\omega + (v_0 + i\delta v_x) ik\} \eta = -i(\omega -kv_0) \eta \tag{32}\]よって\(y=0\)では上側(1)と下側(2)の\(\delta v_y\)の比を取ることで
\[\frac{\delta v_y^{(1)}}{\delta v_y^{(2)}} = \frac{\omega -kv_0^{(1)}}{\omega -kv_0^{(2)}} \tag{33}\]という境界条件が成立していることがわかります。(31), (33)式より\(y \neq 0\)においては
\[\left\{ \begin{array}{l} \delta v_y^{(1)} = (\omega -kv_0^{(1)}) e^{-ky} \\ \delta v_y^{(2)} = (\omega -kv_0^{(2)}) e^{ky} \\ \end{array}\right. \tag{34}\]となることがわかります。
境界面の取り扱い
(29)式の境界面\(y = 0\)での条件を導出しましょう。境界面を挟んで微小区間\([-\epsilon, \epsilon]\)での積分を
\[\Delta_s (f) \equiv \lim_{\epsilon \rightarrow 0} \int_{0-\epsilon}^{0+\epsilon} \frac{\partial f}{\partial y} dy = \lim_{\epsilon \rightarrow 0} \{ f(\epsilon) - f(-\epsilon)\}\]のように定義し、(29)式の両辺を\(y\)に関して微小区間\([-\epsilon, \epsilon]\)で積分することを考えます。
\[\lim_{\epsilon \rightarrow 0} \int_{0-\epsilon}^{0+\epsilon} \frac{\partial}{\partial y} \left\{ (\omega-kv_0) \rho_0 \frac{\partial \delta v_y}{\partial y} + k \rho_0 \delta v_y \frac{\partial v_0}{\partial y}\right\} dy = \Delta_s \left( (\omega-kv_0) \rho_0 \frac{\partial \delta v_y}{\partial y}\right) + \underbrace{\Delta_s \left( k \rho_0 \delta v_y \frac{\partial v_0}{\partial y}\right)}_{=0 \left( \frac{\partial v_0}{\partial y} = 0 (y \neq 0)\right)}\] \[\lim_{\epsilon \rightarrow 0} \int_{0-\epsilon}^{0+\epsilon} k^2 \rho_0 (\omega-kv_0) \delta v_y dy = 0\] \[\begin{aligned} \lim_{\epsilon \rightarrow 0} \int_{0-\epsilon}^{0+\epsilon} \left(\frac{\partial^2}{\partial y^2} -k^2\right) \left( \frac{\delta v_y}{\omega-kv_0}\right) dy &= \lim_{\epsilon \rightarrow 0} \int_{0-\epsilon}^{0+\epsilon} \left\{ \frac{\partial}{\partial y} \frac{\partial}{\partial y} \left( \frac{\delta v_y}{\omega-kv_0}\right) -k^2 \left( \frac{\delta v_y}{\omega-kv_0}\right)\right\} dy \\ &= \lim_{\epsilon \rightarrow 0} \int_{0-\epsilon}^{0+\epsilon} \left\{ \frac{\partial}{\partial y} \left( \frac{\frac{\partial \delta v_y}{\partial y}}{\omega-kv_0} + \frac{k \frac{\partial v_0}{\partial y}}{(\omega-kv_0)^2} \right) -k^2 \left( \frac{\delta v_y}{\omega -kv_0}\right)\right\} dy \\ &= \Delta_s \left( \frac{\frac{\partial \delta v_y}{\partial y}}{\omega-kv_0}\right) + \underbrace{\Delta_s \left( \frac{k \frac{\partial v_0}{\partial y}}{(\omega-kv_0)^2}\right)}_{=0 \left(\frac{\partial v_0}{\partial y} = 0 (y\neq 0)\right)} \end{aligned}\] \[\lim_{\epsilon \rightarrow 0} \int_{0-\epsilon}^{0+\epsilon} \underbrace{\frac{\delta v_y}{\omega-kv_0}}_{(34)} \frac{\partial \rho_0}{\partial y} dy = \lim_{\epsilon \rightarrow 0} \int_{0-\epsilon}^{0+\epsilon} e^{-k \vert y \vert} \frac{\partial \rho_0}{\partial y} dy = e^{-k \vert y \vert} \Delta_s (\rho_0) - \overbrace{\lim_{\epsilon \rightarrow 0} \int_{0-\epsilon}^{0+\epsilon} \rho_0 \underbrace{\frac{\partial}{\partial y} e^{-k \vert y \vert}}_{= \pm k e^{-k \vert y \vert}} dy}^{=0} = \frac{\delta v_y}{\omega-kv_0} \Delta_s (\rho_0)\]より
\[\Delta_s \left\{ (\omega-kv_0) \rho_0 \frac{\partial \delta v_y}{\partial y}\right\} = \frac{k^2 B_0^2}{4\pi} \Delta_s \left( \frac{\frac{\partial \delta v_y}{\partial y}}{\omega-kv_0}\right) + k^2 g \frac{\delta v_y}{\omega-kv_0} \Delta_s (\rho_0) \tag{35}\](34)式を(35)式に代入します。すると
\[\begin{aligned} &\Delta_s \left\{ (\omega-kv_0) \rho_0 \frac{\partial \delta v_y}{\partial y}\right\} = (\omega-kv_0^{(1)}) \rho_0^{(1)} (\omega-kv_0^{(1)}) (-k) e^{-ky} - (\omega-kv_0^{(2)}) \rho_0^{(2)} (\omega-kv_0^{(2)}) ke^{ky} \\ & \xrightarrow{y \rightarrow 0} -k \{ (\omega-kv_0^{(1)})^2 \rho_0^{(1)} + (\omega-kv_0^{(2)})^2 \rho_0^{(2)}\} \end{aligned}\] \[\Delta_s \left( \frac{\frac{\partial \delta v_y}{\partial y}}{\omega- kv_0}\right) = (-k) e^{-ky} - ke^{ky} \ \xrightarrow{y \rightarrow 0} \ -2k\] \[\Delta_s (\rho_0) = \rho_0^{(1)} - \rho_0^{(2)}\]より
\[\begin{align} &-k \{ (\omega-kv_0^{(1)})^2 \rho_0^{(1)} + (\omega-kv_0^{(2)})^2 \rho_0^{(2)}\} = - \frac{k^3 B_0^2}{2\pi} + k^2 g(\rho_0^{(1)} - \rho_0^{(2)}) \notag \\ &\Longrightarrow \ (\rho_0^{(1)} + \rho_0^{(2)}) \omega^2 - 2k (\rho_0^{(1)} v_0^{(1)} + \rho_0^{(2)} v_0^{(2)}) \omega + k^2 (\rho_0^{(1)} (v_0^{(1)})^2 + \rho_0^{(2)} (v_0^{(2)})^2) - \frac{k^2 B_0^2}{2\pi} + kg(\rho_0^{(1)}-\rho_0^{(2)}) = 0 \tag{36} \end{align}\]という式を得ます。これは2次方程式なので、その解の公式から
\[\omega = \frac{k(\rho_0^{(1)} v_0^{(1)} + \rho_0^{(2)} v_0^{(2)})}{\rho_0^{(1)}+ \rho_0^{(2)}} \pm \frac{\sqrt{4k^2 (\rho_0^{(1)} v_0^{(1)} + \rho_0^{(2)} v_0^{(2)})^2 - 4(\rho_0^{(1)} + \rho_0^{(2)}) \left\{ k^2 (\rho_0^{(1)} (v_0^{(1)})^2 + \rho_0^{(2)} (v_0^{(2)})^2) - \frac{k^2 B_0^2}{2\pi} + kg(\rho_0^{(1)} - \rho_0^{(2)})\right\}}}{2 (\rho_0^{(1)}+ \rho_0^{(2)})}\]と求まります。ここで
\[\alpha_1 \equiv \frac{\rho_0^{(1)}}{\rho_0^{(1)} + \rho_0^{(2)}}, \alpha_2 \equiv \frac{\rho_0^{(2)}}{\rho_0^{(1)} + \rho_0^{(2)}}, v_A^2 \equiv \frac{B_0^2}{4\pi \frac{(\rho_0^{(1)} + \rho_0^{(1)})}{2}} = \frac{B_0^2}{2\pi (\rho_0^{(1)} + \rho_0^{(1)})}\]のように定義すると
\[\begin{align} \frac{\omega}{k} &= \alpha_1 v_0^{(1)} + \alpha_2 v_0^{(2)} \pm \sqrt{(\alpha_1 v_0^{(1)} + \alpha_2 v_0^{(2)})^2 - \{ \alpha_1 (v_0^{(1)})^2 + \alpha_2 (v_0^{(2)})^2 \} + v_A^2 - \frac{g}{k} (\alpha_1-\alpha_2)} \notag \\ &= \alpha_1 v_0^{(1)} + \alpha_2 v_0^{(2)} \pm \sqrt{v_A^2 - \alpha_1 \alpha_2 (v_0^{(1)} - v_0^{(2)})^2 - \frac{g}{k} (\alpha_1 - \alpha_2)} \tag{36} \end{align}\]レイリー・テイラー不安定性の条件
磁場がない場合
速度シアと磁場が存在しない、すなわち\(v_0^{(1)} = v_0^{(2)}, v_A = 0\)のとき
\[\frac{g}{k} \frac{\rho_0^{(1)} - \rho_0^{(2)}}{\rho_0^{(1)} + \rho_0^{(2)}} > 0\]ならば\(\omega\)が虚数となり、これは不安定となります。上式が成り立つのは\(\rho_0^{(1)} > \rho_0^{(2)}\)のとき、すなわち上側の流体が下側の流体よりも質量密度が大きく重たい場合であることがわかります。
磁場がある場合
磁場が存在する場合は
\[\frac{g}{k} \frac{\rho_0^{(1)} - \rho_0^{(2)}}{\rho_0^{(1)} + \rho_0^{(2)}} > v_A^2\]ならば不安定となります。これは磁気張力が、摂動により波打った境界面をもとに戻そうとする方向に働くためです。
成長しやすい波長
簡単のため、磁場がない場合を考えましょう。もし、上述の不安定条件が満たされている場合
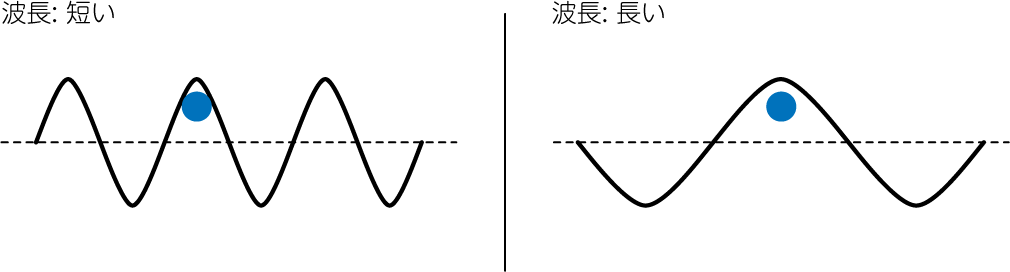
\[\frac{\omega}{k} = \alpha_1 v_0^{(1)} + \alpha_2 v_0^{(2)} \pm \sqrt{-\frac{g}{k} (\alpha_1 - \alpha_2)} = \frac{\omega_\mathrm{Re} + i \omega_\mathrm{Im}}{k}\]のように書くと、\(\omega_\mathrm{Im} \propto k^{1/2} \propto \lambda^{-1/2}\)とわかります。よって波長が短いゆらぎほど、速く成長することがわかります。 これは下図のように、波打つ境界面の下側の軽い流体要素(青丸)の周囲がどれだけ上側の重たい流体に囲まれているかによって浮力の感じ方が変わることから理解することができます。同じ高さ\(y\)にある青丸でも、下右図は上側の流体に囲まれていないことから、浮力を感じにくいことがわかります。
ただし、磁場があるとその曲率による磁気張力も考慮する必要があるため、その兼ね合いから不安定性の成長率を考える必要があります。
ケルビン・ヘルムホルツ不安定性の条件
磁場がない場合
一様重力と磁場が存在しない、すなわち\(g = 0, v_A = 0\)のとき
\[\alpha_1 \alpha_2 (v_0^{(1)} - v_0^{(2)})^2 > 0\]ならば不安定となります。この解析では\(v_0^{(1)} \neq v_0^{(2)}\)ならば(速度シアが存在するならば)左辺は必ず正の値となるため、不安定であることがわかります。
磁場がある場合
磁場が存在する場合は
\[\alpha_1 \alpha_2 (v_0^{(1)} - v_0^{(2)})^2 > v_A^2\]ならば不安定です。これは磁場がある場合のレイリー・テイラー不安定性と同じ理由から、磁場が安定化させる働きをします。
リチャードソン数
以下では磁場が存在せず、一様重力\(g\)において層を成している2流体を考えましょう。人間が適当に、境界面付近の下側の流体要素を\(\delta y\)だけ上に持ち上げたとします。 このとき、流体要素の密度が上側の流体に仲間入りし、その密度が\(\rho_0^{(2)}\)に変化したとします。このとき、人間が重力に逆らってした仕事は
\[\delta W = -g (\rho_0^{(2)} - \rho_0^{(1)}) \delta y\]のように書けます。またこのときの運動エネルギーの変化量は、持ち上げたことによる混合の効果により\(\rho_0^{(1)} + \rho_0^{(2)}\)の質量の流体要素の塊が運動していると代表させて考えると
\[\frac{1}{2} (\rho_0^{(1)} + \rho_0^{(2)}) \left( \frac{\rho_0^{(1)} v_0^{(1)} + \rho_0^{(2)} v_0^{(2)}}{\rho_0^{(1)} + \rho_0^{(2)}}\right)^2 - \frac{1}{2} \rho_0^{(1)} (v_0^{(1)})^2 - \frac{1}{2} \rho_0^{(2)} (v_0^{(2)})^2 = - \frac{1}{2} \frac{\rho_0^{(1)}\rho_0^{(2)}}{\rho_0^{(1)} + \rho_0^{(2)}} (v_0^{(1)} - v_0^{(2)})^2\]のようになります。最右辺は必ず負の値なので、流体の運動エネルギーは減少することがわかります。人間がした仕事よりも運動エネルギーの変化量が大きければ、この交換は可能と考えることができるので、ケルビン・ヘルムホルツ不安定性が起こるための必要条件は
\[\frac{1}{2} \frac{\rho_0^{(1)}\rho_0^{(2)}}{\rho_0^{(1)} + \rho_0^{(2)}} (v_0^{(1)} - v_0^{(2)})^2 > -g (\rho_0^{(2)} - \rho_0^{(1)}) \delta y\]ここで持ち上げた距離\(\delta y\)は微小で、\(\rho_0^{(2)} = \rho_0^{(1)} + \delta \rho, v_0^{(2)} = v_0^{(1)} + \delta v\)のように書くと
\[\frac{1}{2} \frac{\rho_0^{(1)} (\rho_0^{(1)} + \delta \rho)}{\rho_0^{(1)} + \rho_0^{(1)} + \delta \rho} (-\delta v)^2 \simeq \frac{1}{4} \rho_0^{(1)} \delta v^2 > -g \delta \rho \delta y\]両辺を\(\delta y^2\)で割ると
\[\frac{1}{4} \rho_0^{(1)} \left( \frac{\delta v}{\delta y}\right)^2 > - g \frac{\delta \rho}{\delta y}\]と整理されます。速度場や密度が連続的に変化しているとして、\(\delta y\)で割られている量を微分として考えると、ケルビン・ヘルムホルツ不安定性が起こる条件は
\[J \equiv - \frac{g}{\rho} \frac{d\rho/dy}{(dv/dy)^2} < \frac{1}{4}\]この\(J\)をリチャードソン数 (Richardson number)と呼びます。速度勾配\(\frac{dv}{dy}\)が大きくなるほど\(J\)は小さくなるため、ケルビン・ヘルムホルツ不安定性が起こりやすくなります。
レイリー・テイラー不安定性の例: 超新星爆発内部と超新星残骸残骸
質量の大きい恒星は、その生涯の最期に超新星爆発を起こします。このとき、星間空間に伝わる衝撃波が圧縮した星間物質と、超新星爆発を起こした恒星からの衝撃波圧縮された噴出物(エジェクタ)部分が接する部分でレイリー・テイラー不安定性が起こるとされています。

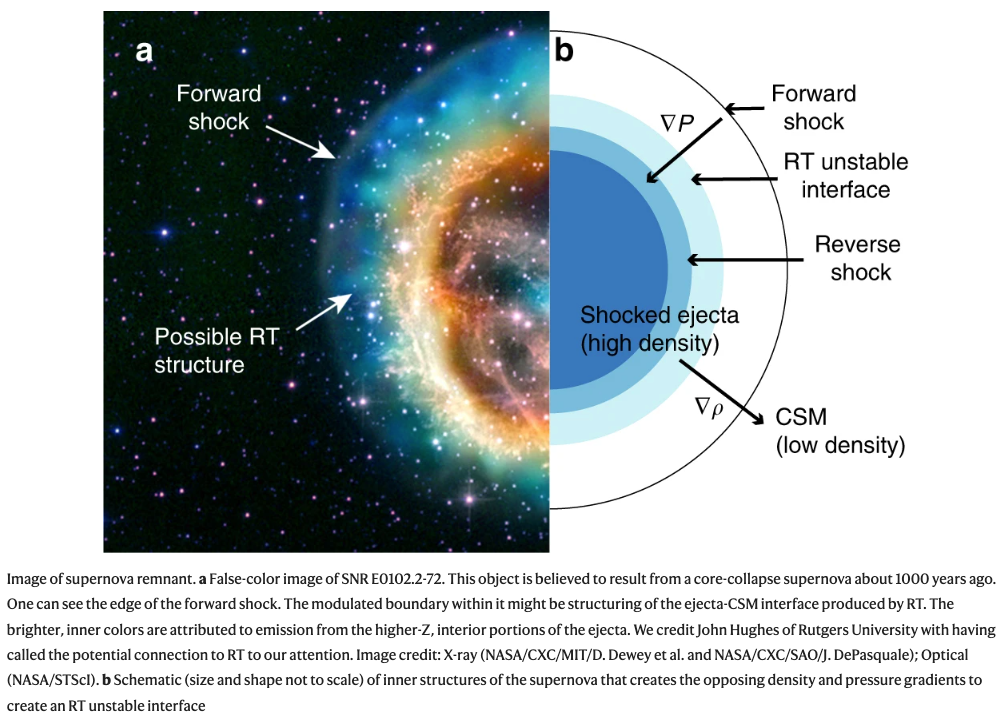
そして下図はこれを実際に数値シミュレーションで実証したものです。
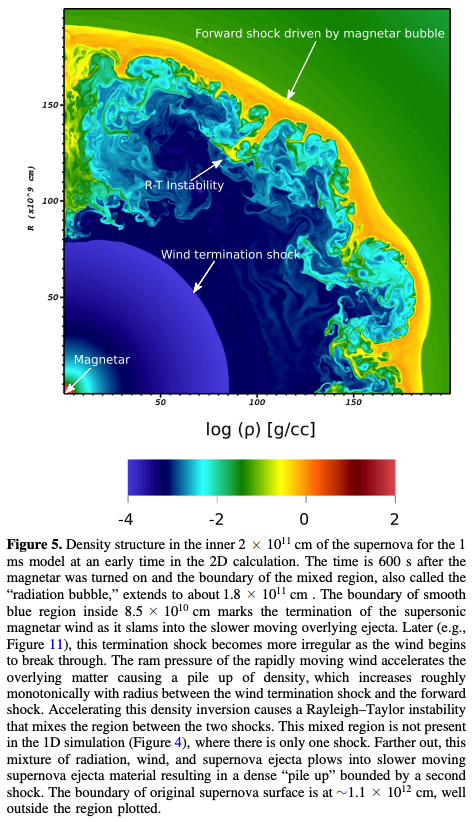
また星間空間内を伝播していく衝撃波面も最終的にレイリー・テイラー不安定性を起こすとされています。最初はその超新星爆発の爆風の勢いから自由膨張していた超新星爆発の衝撃波面ですが、徐々に星間物質がその衝撃波面に降り積もって行くことで、波面は減速します。 衝撃波面に乗った観測者から見ていると、このブレーキは衝撃波面に対して外向きの加速度を受けているような慣性力として働きます。衝撃波により圧縮された星間物質の外側には、圧縮されていない希薄な星間物質が存在するため、この慣性力によるレイリー・テイラー不安定性が起こると言われています。

ケルビン・ヘルムホルツ不安定性の例: 宇宙ジェット
宇宙空間に存在するブラックホールからは相対論的な速度でガスが噴出しています。それが周囲の星間物質との速度シアにより混合されることが知られています。下図はEHTで超大質量ブラックホールが撮像されたことでも有名なM87のジェットにおける構造を観測したものです。
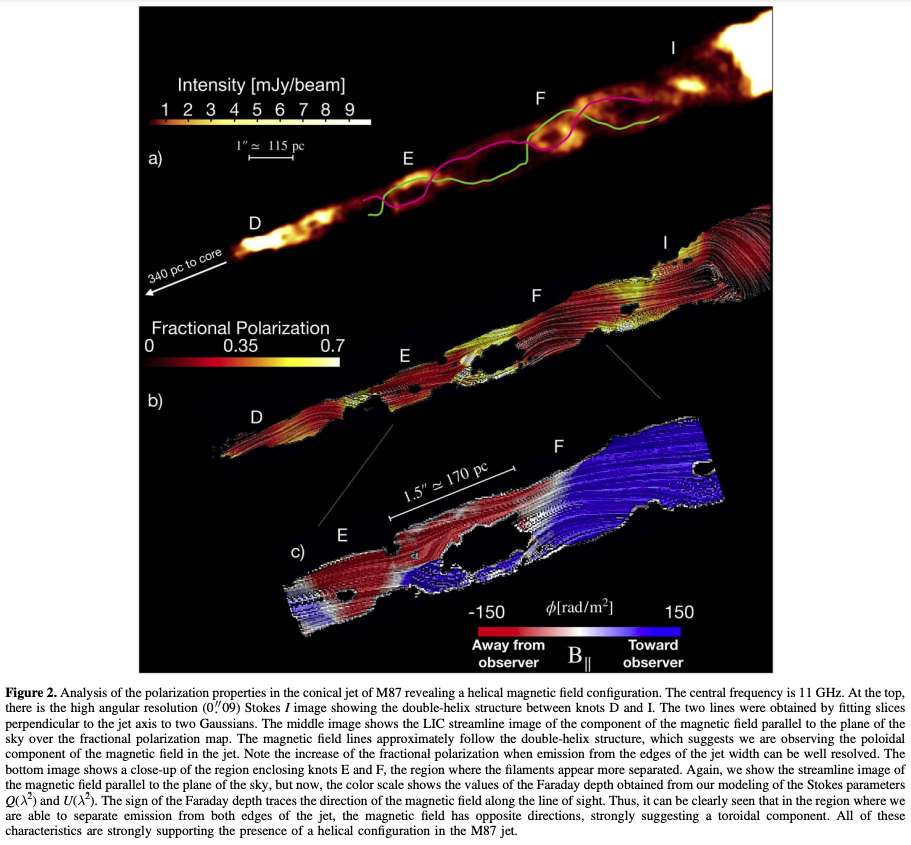
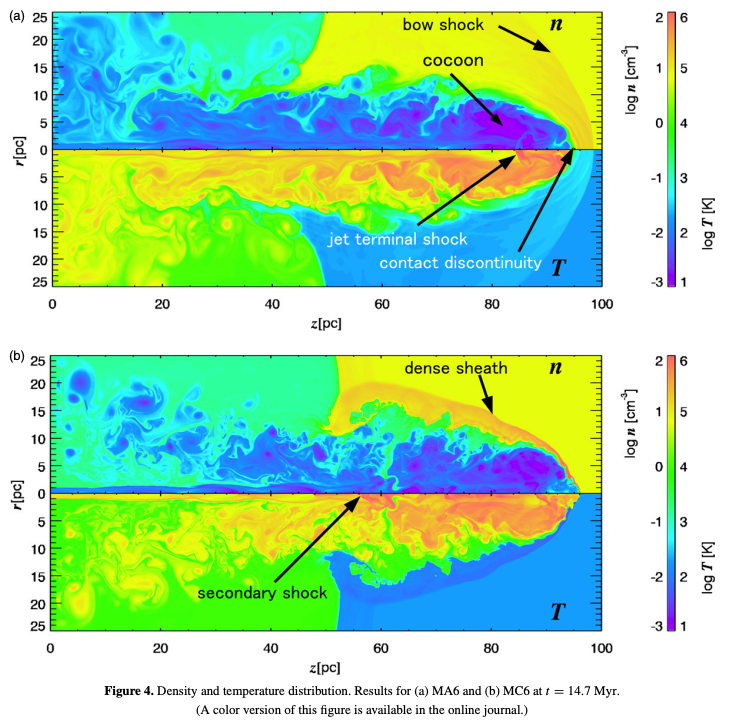
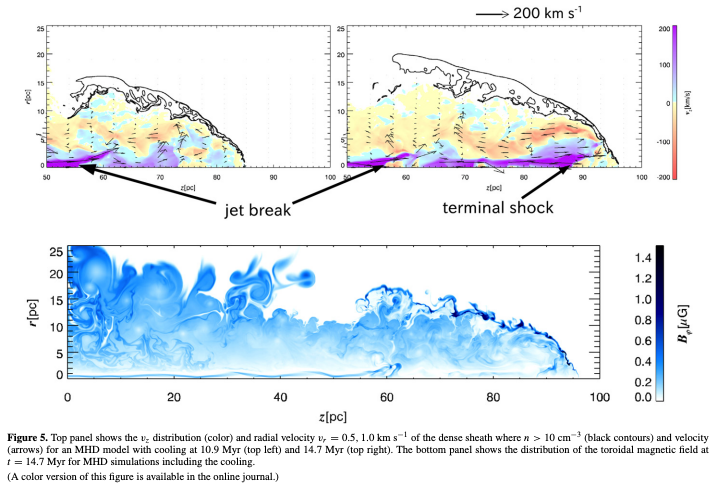
またここで発生するケルビン・ヘルムホルツ不安定性が磁場を強めることが、シミュレーションからも示されています。
参考文献
[1] 観山 正見, 野本 憲一, 二間瀬 敏史, ”天体物理学の基礎 II”
[2] 福江純, 和田圭一, 梅村雅之, ”宇宙流体力学の基礎”
[3] 福井康雄, 犬塚修一郎, 大西利和, 中井直正, 舞原俊憲, 水野亮, “星間物質と星形成”
[4] S. Chandrasekhar, “Hydrodynamic and Hydromagnetic Stability”
[5] E. Priest, “Solar MagnetohydroDynamics”
[6] Kuranz et al., 2018, “How high energy fluxes may affect Rayleigh-Taylor instability growth in young supernova remnants”
[7] Chen et al., 2016, “Magnetar-Powered Supernovae in Two Dimensions. I. Superluminous Supernovae”
[8] Pasetto et al., 2021, “Reading M87’s DNA: A Double Helix revealing a large scale Helical Magnetic Field”
[9] Asahina et al., 2014, “Magnetohydrodynamic Simulations of a Jet Drilling an HI Cloud: Shock Induced Formation of Molecular Clouds and Jet Breakup”