Table of contents
スペクトル線形成
スペクトル線に対する輻射輸送
ある吸収線は電子のエネルギー準位の遷移により発生しますが、その過程は共鳴散乱(resonance scattering)と真の吸収(あるいは純粋な吸収, true (or pure) absoption)とに分類することができます。 共鳴散乱では、吸収により高いエネルギー準位に戦死した電子がすぐに元の準位に戻るため、吸収した光と同じ波長の光を放出します。 散乱は等方的に起こるため、ある方向から見ている場合には、この散乱により光の強度が減少し、吸収線が形成されます。 しかし真の吸収の場合は、光子を吸収して電子が高いエネルギー準位に上がった直後にその原子(またはイオン)が他の粒子と衝突をしてエネルギーを分け与え、電子が下のエネルギー準位に遷移する、という過程を経ます。 吸収によって得たエネルギーは衝突した粒子の運動エネルギーに変換されます。 すなわち、光子は壊されて、熱エネルギーとなるのです。
以下では、吸収係数と散乱係数に対して以下のような分類を行いましょう。
- \(\kappa_c\): 吸収線の振動数における連続吸収係数
- \(\sigma\): 吸収線の振動数における連続散乱係数
- \(\sigma_\nu\): 吸収線の共鳴散乱係数
- \(\kappa_\nu\): 吸収線の真の吸収係数
これらを用いると、輻射輸送の式は
\[\frac{\mu}{\rho} \frac{dI_\nu}{dz} = - (\kappa_\nu + \kappa_c + \sigma_\nu + \sigma) I_\nu + (\kappa_c + \kappa_\nu) B_\nu + (\sigma + \sigma_\nu) J_\nu \tag{5.36}\]のように書くことができます。 ここで、発光係数\(\eta = \eta_\nu^t + \eta_\nu^s\)に対して、\(\eta^t = (\kappa_c + \kappa_\nu) B_\nu, \eta^s = (\sigma + \sigma_\nu) J_\nu\)を用いました。 さらに光学的厚み
\[d\tau_\nu = -\rho (\kappa_\nu + \kappa_c + \sigma + \sigma_\nu) dz \tag{5.37}\]を用いると、(5.36)式は
\[\mu \frac{dI_\nu}{d\tau_\nu} = I_\nu - \frac{(\kappa_c + \kappa_\nu)}{\kappa_c + \kappa_\nu + \sigma + \sigma_\nu} - \frac{(\sigma + \sigma_\nu) J_\nu}{\kappa_c + \kappa_\nu + \sigma + \sigma_\nu} \tag{5.38}\]となります。 ここで
\[\lambda_\nu \equiv \frac{\kappa_c + \kappa_\nu}{\kappa_c + \kappa_\nu + \sigma + \sigma_\nu} \tag{5.39}\]を定義すると、(5.38)式は
\[\mu \frac{dI_\nu}{d\tau_\nu} = I_\nu -\lambda_\nu B_\nu - (1-\lambda_\nu) J_\nu \tag{5.40}\]のように表現することができます。 \(\lambda_\nu B_\nu\)は熱放射に由来する成分、そして\((1-\lambda_\nu) J_\nu\)が散乱に由来する成分として表れています。 後半部分を\(S_\nu = \lambda_\nu B_\nu + (1-\lambda_\nu) J_\nu\)のように源泉項としてまとめれば、\(S_\nu\)によって放射強度\(I_\nu\)が変化する式と見ることもできます。 (5.40)式はミルン・エディントン方程式 (Milne-Eddington equation)として知られています。
ミルン・エディントン模型 (Milne-Eddington Model)
簡単のために、\(\lambda_\nu\)が場所に依存せず一定であるとします。 また\(B_\nu = B_0 + B_1 + \tau\)のように、プランク関数\(B_\nu\)は連続光に対する光学的厚み\(\tau \ (d\tau = - \rho (\kappa_c + \sigma) dz)\)の線形関数であると仮定しましょう。 すると(5.37)式から
\[B_\nu = B_0 + B_1 \tau_\nu \frac{\kappa_c + \sigma}{\kappa_\nu + \sigma_\nu + \kappa_c + \sigma} = B_0 + p_\nu \tau_\nu \qquad \left( p_\nu \equiv \frac{\kappa_c + \sigma}{\kappa_\nu + \sigma_\nu + \kappa_c + \sigma} B_1\right) \tag{5.41}\]のように変形されます。 ここでさらに、\(p_\nu\)も場所に依存しないと仮定します。
吸収線内と連続光に対するextinction (吸収と散乱)の比を
を定義すると、\(p_\nu\)は
\[p_\nu = \frac{B_1}{1 + \beta_\nu}\]のようになります。 もし\(\beta_\nu = 0\)のときは、\(p_\nu = B_1\)であり、
\[\frac{d\tau}{d\tau_\nu} = \frac{\kappa_c + \sigma}{\kappa_\nu + \sigma_\nu + \kappa_c + \sigma}\]から、これは\(\tau_\nu = \tau\)、すなわち吸収線のない連続光に対する光学的厚みとなります。
(5.40)式を全立体角積分すると、\(J_\nu = \frac{1}{4\pi} \int_{4\pi} I_\nu d\Omega, F_\nu = \frac{1}{4\pi} \int_{4\pi} \mu I_\nu d\Omega\)より
を得ます。 また(5.40)式に\(\mu\)をかけたものを全立体角で積分すると、\(K_\nu = \frac{1}{4\pi} \int_{4\pi} \mu^2 I_\nu d\Omega\)より
\[\frac{dK_\nu}{d\tau_\nu} = \frac{1}{4\pi} F_\nu \tag{5.83}\]となります。 この式を\(\tau_\nu\)で微分し、エディントン近似\(K_\nu = J_\nu /3\)を用いると
\[4\pi \frac{d^2 K_\nu}{d\tau_\nu^2} = \frac{dF_\nu}{d\tau_\nu} \underbrace{=}_{(5.42)} 4\pi \lambda_\nu (J_\nu - B_\nu) \ \Longrightarrow \ \frac{1}{3} \frac{d^2 J_\nu}{d\tau_\nu^2} = \lambda_\nu (J_\nu - B_\nu) \tag{5.44}\]のように計算されます。 (5.41)式の仮定から\(\frac{d^2 B_\nu}{d\tau_\nu^2} = 0\)なので、この式は
\[\frac{d^2}{d\tau_\nu^2} (J_\nu - B_\nu) = 3\lambda_\nu (J_\nu - B_\nu) \tag{5.45}\]のように書くことができます。 この方程式の一般解は
\[J_\nu - B_\nu = C_1 e^{-\sqrt{3\lambda_\nu} \tau_\nu} + C_2 e^{\sqrt{3\lambda_\nu} \tau_\nu} \tag{5.46}\]です。 ただし、\(\tau_\nu \rightarrow \infty\)で\(J_\nu \rightarrow B_\nu\)という境界条件から、\(C_2 = 0\)であることがわかります。
\(C_1\)を得るために、\(\tau_\nu = 0\)での境界条件を考えましょう。 この境界でもエディントン近似\(K_\nu = J_\nu / 3\)が成り立つとします。 そのような放射場として
のように、外向きに放射が出ていくような場合が考えられます。 この近似を用いると
\[\begin{align} &J_\nu (0) = \frac{1}{4\pi} \int_{4\pi} I_\nu (0) d\Omega = \frac{I_0}{2} \int_0^1 d\mu = \frac{I_0}{2}, \quad F_\nu (0) = \int_{4\pi} \mu I_\nu (0) d\Omega = 2\pi I_0 \int_0^1 \mu d\mu = \pi I_0 \notag \\ &\Longrightarrow \ J_\nu (0) = \frac{F_\nu (0)}{2\pi} \tag{5.48} \end{align}\]のように計算されます。 この関係式とエディントン近似を(5.43)式に用いると
\[\begin{align} &4\pi \left. \frac{dK_\nu}{d\tau_\nu} \right|_{\tau_\nu=0} = \frac{4\pi}{3} \left. \frac{dJ_\nu}{d \tau_\nu} \right|_{\tau_\nu=0} = F_\nu(0) = 2\pi J_\nu (0) \underbrace{=}_{(5.46)} 2\pi (B_\nu (0) + C_1) \notag \\ &\underbrace{\Longrightarrow}_{(5.41)} \left. \frac{d J_\nu}{d\tau_\nu} \right|_{\tau_\nu = 0} = \frac{3}{2} (B_0 + C_1) \tag{5.49} \end{align}\]のようになります。 一方で、(5.41), (5.46)式より
\[\left. \frac{dJ_\nu}{d\tau_\nu} \right|_{\tau_\nu = 0} = p_\nu - C_1 \sqrt{3\lambda_\nu} \tag{5.50}\]となるので
\[C_1 = \frac{p_\nu - \frac{3}{2} B_0}{\sqrt{3 \lambda_\nu} + \frac{3}{2}} \tag{5.51}\]が得られます。 以上から
\[J_\nu (\tau_\nu) = B_\nu (\tau_\nu) + \frac{p_\nu - \frac{3}{2} B_0}{\sqrt{3 \lambda_\nu} + \frac{3}{2}} e^{-\sqrt{3\lambda_\nu} \tau_\nu} = B_0 + p_\nu \tau_\nu + \frac{p_\nu - \frac{3}{2} B_0}{\sqrt{3 \lambda_\nu} + \frac{3}{2}} e^{-\sqrt{3\lambda_\nu} \tau_\nu} \tag{5.52}\]のようになります。 (5.48)式を用いると、恒星表面から出てくるフラックスは
\[F_\nu (0) = 2\pi \left( B_0 + \frac{p_\nu - \frac{3}{2} B_0}{\sqrt{3 \lambda_\nu} + \frac{3}{2}} \right) = 2\pi \frac{\sqrt{3\lambda_\nu} B_0 + p_\nu}{\sqrt{3\lambda_\nu} + \frac{3}{2}} \tag{5.53}\]と計算されます。 連続フラックス\(F_c (0)\)は、(5.53)式で\(\kappa_\nu \rightarrow 0, \sigma_\nu \rightarrow 0\)に対応するので、\(p_{\nu, \mathrm{continuum}} \rightarrow B_1, \lambda_{\nu, \mathrm{continuum}} \rightarrow \frac{\kappa_c}{\kappa_c + \sigma} \equiv \epsilon\)のように書き換えることで得られます。
\[F_c (0) = 2\pi \frac{B_1 + B_0 \sqrt{3\epsilon}}{\sqrt{3\epsilon} + \frac{3}{2}} \tag{5.54}\]したがって、スペクトル線中のresidual flux \(R_\nu = F_\nu (0) / F_c (0)\)は
\[R_\nu = \frac{\sqrt{3\lambda_\nu} B_0 + p_\nu}{\sqrt{3\lambda_\nu} + \frac{3}{2}} \frac{\sqrt{3\epsilon} + \frac{3}{2}}{B_1 + B_0 \sqrt{3\epsilon}} \tag{5.55}\]のように書かれます。
散乱によって形成される吸収線
ここでは、連続光に対して散乱が存在しない場合を考えましょう。 すなわち\(\sigma = 0\)より\(\lambda_{\nu, \mathrm{continuum}} = \epsilon = 1\)となります。 そして吸収線に対しては散乱のみがはたらくとします。 すると吸収\(\kappa_\nu = 0\)より、\(\lambda_\nu = \frac{\kappa_c}{\kappa_c + \sigma_\nu}, p_\nu = B_1 \frac{\kappa_c}{\sigma_\nu + \kappa_c}\)です。 この条件において、residual flux (5.55)式は
\[R_\nu = \frac{\sqrt{\frac{3\kappa_c}{\kappa_c + \sigma_\nu}} B_0 + \frac{\kappa_c}{\kappa_c + \sigma_\nu} B_1}{\sqrt{\frac{3\kappa_c}{\kappa_c + \sigma_\nu}} + \frac{3}{2}} \frac{\sqrt{3} + \frac{3}{2}}{B_1 + B_0 \sqrt{3}} \tag{5.56}\]のようになります。 強い吸収線の極限\(\sigma_\nu \gg \kappa_c\)では、\(R_\nu \rightarrow 0\)となります。 これは、散乱により形成される非常に強い吸収線の中心部(core部分)は、真っ暗になることがわかります。
吸収過程のみよって形成される吸収線
ここでも連続光に対しては散乱がない、すなわち\(\sigma = 0, \epsilon = 1\)を仮定します。 しかし今度は、吸収線では吸収だけしかない\(\sigma_\nu = 0\)としましょう。 このとき\(\lambda_\nu = 1, p_\nu = \frac{\kappa_c}{\kappa_\nu + \kappa_c} B_1\)です。 すると(5.55)式は
\[R_\nu = \frac{\sqrt{3} B_0 + \frac{\kappa_c}{\kappa_\nu + \kappa_c} B_1}{\sqrt{3} + \frac{3}{2}} \frac{\sqrt{3} + \frac{3}{2}}{B_1 + B_0 \sqrt{3}} = \frac{\sqrt{3} B_0 + \frac{\kappa_c}{\kappa_\nu + \kappa_c} B_1}{B_1 + B_0 \sqrt{3}} \tag{5.57}\]となります。 この場合、\(\kappa_\nu \gg \kappa_c\)に対しての吸収線のresidual fluxはゼロにならずに有限の値となります。
\[R_0 = R_\nu (\sigma_\nu = 0, \kappa_\nu / \kappa_c \rightarrow \infty) = \frac{1}{1 + \frac{B_1}{\sqrt{3} B_0}} \tag{5.58}\]\(\kappa_\nu / \kappa_c \rightarrow \infty\)のとき、表面しか見ることができず、表面のプランク関数\(B_\nu [T(\tau_\nu = 0)]\)を見ていることを意味します。 これに対して、先程のような非常に強い散乱によるスペクトル線の場合は、私たち観測者の方向に向かう光が幾度となく散乱されます。 このため、観測者方向に向かう光が来なくなり、真っ暗になるのです。
Center-to-Limb Variations
太陽の観測では、fluxではなくintensityが観測されます。 表面のintensity \(I_\nu (0, \mu)\)は、平行平板近似の式より
\[I_\nu^+ (0, \mu) = \int_0^\infty S_\nu (t) e^{-t/\mu} \frac{dt}{\mu} \tag{5.59}\]のように書かれます。 源泉関数\(S_\nu\)は、(5.40), (5.52)式より
\[\begin{align} S_\nu (\tau_\nu) &= \lambda_\nu B_\nu + (1-\lambda_\nu) J_\nu = B_\nu + (1-\lambda_\nu) (J_\nu - B_\nu) \notag \\ &= B_0 + p_\nu \tau_\nu + \frac{(1-\lambda_\nu) \left( p_\nu - \frac{3}{2} B_0\right)}{\sqrt{3\lambda_\nu} + \frac{3}{2}} e^{-\sqrt{3\lambda_\nu} \tau_\nu} \tag{5.60} \end{align}\]となります。 この式を(5.59)式に代入すると
\[I_\nu^+ (0, \mu) = B_0 + p_\nu \mu + \frac{(1-\lambda_\nu) \left( p_\nu -\frac{3}{2} B_0\right)}{\left( \sqrt{3\lambda_\nu} + \frac{3}{2} \right) (\sqrt{3\lambda_\nu} \mu + 1)} \tag{5.61}\]連続光(\(\kappa_\nu =0, \sigma_\nu = 0\))に対しては、\(p_\nu = B_1\)です。 また連続光に対する散乱を無視すると、\(\sigma = 0\)より\(\lambda_\nu = 1\)となるので
\[I_c^+ (0, \mu) = B_0 + B_1 \mu \tag{5.62}\]と求まります。
地球から太陽を観測すると、太陽表面が有限の大きさで観測されます。 このことから、吸収線の輪郭は中心からの角距離\(\theta\)に依存し、吸収線中のresidual intensityは\(r_\nu (\mu) = I_\nu^+ (0, \nu) / I_c^+ (0, \nu)\)で与えられます。 連続光に対する散乱を無視し(\(\sigma = 0\))、吸収線も純粋な吸収によってのみ形成される(\(\sigma_\nu = 0\))とすると、\(\lambda_\nu = 1, p_\nu = \frac{B_1}{1+\kappa_\nu / \kappa_c}\)より
さらに\(\kappa_\nu \gg \kappa_c\)、すなわち吸収線での真の吸収係数の方が支配的であるとすると
\[r_\nu (\mu) \simeq \frac{B_0}{B_0 + B_1 \mu} \tag{5.63}\]のようになります。 この式から、太陽の縁 (limb領域; \(\mu \sim 0\))では\(r_\nu \rightarrow 1\)となり、吸収線が消えることがわかります。 これは、\(\mu \sim 0\)では\(\tau_\nu \sim 0\)からの光しか私たちに届かない、太陽の周縁減光から理解することができます。
また、吸収線が純粋に散乱だけで形成される場合についても考えてみましょう。 鎖きほどと同様に連続光に対する散乱の影響は無視し、\(\sigma = 0\)とします。 このとき、\(\kappa_\nu \ll \sigma_\nu\)より、\(\lambda_\nu = 0, p_\nu = \frac{B_1}{1+\sigma_\nu / \kappa_c}\)です。 すると
さらに\(\sigma_\nu \gg \kappa_c\)、すなわち吸収線での散乱の方が優勢であるとすると
\[r_\nu (\mu) \simeq \frac{\mu + 2/3}{B_0 + B_1 \mu} \frac{\kappa_c}{\sigma_\nu} B_1 \sim 0 \tag{5.64}\]で、\(\mu\)の値に関わらずゼロになります。 これは多数の散乱により私たちの方向に向かう光がなくなるという、先程の説明に一致します。
吸収線の成長曲線 (curve of growth)
吸収線の成長曲線とは、吸収線の等価幅(equivalent width)が、その吸収線を作る粒子の数の増加とともにどのように大きくなるかを表す曲線です。 この曲線は、等価幅の観測値から、恒星大気の元素組成を推定するのに用いられてきました。 以下では、散乱過程が重要でない場合だけを考え、\(\sigma_\nu = 0, \sigma=0\)とします。 このとき、\(\lambda_\nu = 1, \beta_\nu = \kappa_\nu / \kappa_c, p_\nu = B_1 / (1+ \kappa_\nu / \kappa_c)\)です。 そして、スペクトル線の輪郭は(5.57)式で与えられます。 すると、吸収線の深さは
\[A_\nu = 1 - R_\nu = B_1 \frac{1 - \frac{\kappa_c}{\kappa_\nu + \kappa_c}}{B_0 \sqrt{3} + B_1} = \frac{\frac{\beta_\nu}{1 + \beta_\nu}}{1 + \frac{\sqrt{3} B_0}{B_1}} \tag{5.65}\]と表されます。 強い吸収線の極限\(\beta_\nu \rightarrow \infty\)での値を
\[A_0 \equiv \frac{1}{1 + \frac{\sqrt{3} B_0}{B_1}} \tag{5.66}\]のように定義すると
\[A_\nu = \frac{\beta_\nu}{1+\beta_\nu} A_0 \tag{5.67}\]のように書かれます。 従って、等価幅は
\[W_\nu = \int_0^\infty A_\nu d\nu = A_0 \int_0^\infty \frac{\beta_\nu}{1+\beta_\nu} d\nu \tag{5.68}\]と表されます。 振動数\(\nu\)の代わりにドップラー幅\(\Delta \nu_D = \nu_0 \xi_0 / c\)を単位にした、線中央からの距離
\[v \equiv \frac{\nu - \nu_0}{\Delta \nu_D} \tag{5.69}\]を用いて積分を行いましょう (\(\xi_0\)は熱運動の典型的な速度\(\xi_0 = \sqrt{2k_B T/m}\)を表し、マクスウェル分布は\(e^{-\xi^2 / \xi_0^2}\)に比例します)。 すると
\[W_\nu = A_0 \int_{-\infty}^\infty \frac{\beta_\nu}{1+\beta_\nu} d(\nu - \nu_0) = 2 A_0 \Delta \nu_D \int_{0}^\infty \frac{\beta (v)}{1+\beta (v)} dv \tag{5.70}\]のように計算できます。 途中、吸収線の左右対称性を用いました。 さらに\(\beta (v)\)をフォークト関数\(H(a, v) (a = \Gamma / (4\pi \Delta \nu_D))\)を用いて
\[\beta(v) = \frac{\kappa_\nu}{\kappa_c} = \frac{\kappa_\nu \rho}{\kappa_c \rho} = \frac{\alpha_\nu}{\kappa_c \rho} = \frac{\sqrt{\pi} e^2 f}{m c \Delta \nu_D \kappa_c \rho} H(a, v) = \beta_0 H(a, v) \tag{5.71}\]のように表しましょう。 すると(5.70)式は
\[W^\ast (a, \beta_0) = \frac{W_\nu}{2 A_0 \Delta \nu_D} = \beta_0 \int_0^\infty \frac{H(a, v)}{1 + \beta_0 H(a, v)} dv \tag{5.72}\]のように書くことができます。 フォークト関数\(H(a, v)\)は、概略的に
\[H(a, v) \simeq \left\{ \begin{array}{ll} e^{-v^2} & v \ll 1 \\ a / (\sqrt{\pi} v^2) & v \gg 1 \end{array} \right.\]のように表されるのでした。 \(v \ll 1\)は吸収線の中央部(core)の振る舞い、\(v \gg 1\)はwing部分の振る舞いを表しています。
- \(\beta_0 < 1\) (弱い吸収線)のとき
弱い吸収線の場合、等価幅には吸収線のcore部分が大きな寄与をし、wingの部分は重要でなくなります。 ここでは、弱い吸収線\(\beta_0 < 1\)に対してcoreの部分だけを考えることにしましょう。 すなわち\(\beta(v) \simeq \beta_0 e^{-v^2}\)のように書くと
\[\begin{align} W^\ast &\simeq \beta_0 \int_0^\infty \frac{e^{-v^2}}{1+\beta_0 e^{-v^2}} dv \underbrace{\simeq}_{分母をテイラー展開} \beta_0 \int_0^\infty e^{-v^2} (1-\beta_0 e^{-v^2} + \cdots) dv \notag \\ &\underbrace{\simeq}_{ガウス積分} \frac{\sqrt{\pi}}{2} \beta_0 \left( 1 - \frac{\beta_0}{\sqrt{2}} + \cdots \right) \tag{5.73} \end{align}\]のように計算されます。 (5.73)式は、弱い吸収線(\(\beta_0\)が小さい)の等価幅には、\(\beta_0\)に線形に比例する部分が重要であることを示しています。 この場合、\(W^\ast \propto \beta_0 \propto \kappa_\nu / \kappa_c \propto N_i / N_H\)のように書けることから、等価幅は吸収する粒子の数に比例して大きくなるとわかります。 成長曲線のこの部分は線形部(linear part)として知られます。 また、この線形部では\(\beta_0 \propto 1/ \Delta \nu_d\)であり、\(W^\ast \propto W/ \Delta \nu_D\)から、等価幅\(W\)は\(\Delta \nu_D\)に依存しません。
- \(\beta_0 \gg 1\) (強い吸収線)のとき
次に\(\beta_0\)が大きく、吸収線の中心では極限の暗さになっていますが、まだwingの寄与が小さい場合を考えましょう。 このときも弱い吸収線の場合と同様に\(\beta (v) = \beta_0 e^{-v^2}\)のように書くと
\[W^\ast \simeq \int_0^\infty \frac{e^{-v^2}}{1+\beta_0 e^{-v^2}} dv\]と書かれます。 ここで\(u = v^2, dv = u^{-1/2} du / 2\)のように変数変換を行い、さらに\(\beta_0 = e^\alpha\)のように書くと
\[W^\ast = \frac{1}{2} \int_0^\infty \frac{e^{\alpha -u}}{1+e^{\alpha - u}} \frac{du}{\sqrt{u}} = \frac{1}{2} \left( \int_0^\alpha \frac{e^{\alpha -u}}{1+e^{\alpha - u}} \frac{du}{\sqrt{u}} + \int_\alpha^\infty \frac{e^{\alpha -u}}{1+e^{\alpha - u}} \frac{du}{\sqrt{u}} \right)\]と変形できます。 第2項の\(\alpha \leq u \leq \infty\)の積分範囲においては、\(e^{\alpha - u} \ll 1\)のため、積分値が小さくなることが予想されます。 よって第2項は無視し、第一項だけを計算していきましょう。 第一項においても、\(\beta_0 = e^\alpha \gg 1\)であることから、\(\alpha \gg u\)の部分が積分に大きく寄与すると考えると、\(e^{\alpha - u} \gg 1\)より
\[W^\ast \simeq \frac{1}{2} \int_0^\alpha \frac{du}{\sqrt{u}} = \sqrt{\alpha} = \sqrt{\ln \beta_0} \tag{5.74}\]のように計算されます。 以上から
\[W \simeq 2 A_0 \Delta \nu_D \sqrt{\ln \beta_0} \tag{5.75}\]となり、\(\beta_0\)に対して等価幅\(W\)は\(\sqrt{\beta_0}\)の依存しかありません。 そのため、成長曲線のこの領域は飽和部(saturation part)と呼ばれます。
さらに吸収を起こす原子やイオン数が増し、さらに\(\beta_0\)が大きくなった場合を考えましょう。 するとcoreだけでなく、wingでの吸収も重要になります。 このとき、フォークト関数は
と近似できることから、(5.72)式は
\[\begin{align} \frac{W}{2 A_0 \Delta \nu_D} &\simeq \int_0^\infty \frac{\frac{\beta_0 a}{\sqrt{\pi} v^2}}{1 + \frac{\beta_0 a}{\sqrt{\pi} v^2}} = \int_0^\infty \frac{dv}{\frac{\sqrt{\pi}}{\beta_0 a} v^2 + 1} \underbrace{=}_{\sqrt{\frac{\sqrt{\pi}}{\beta_0 a}} v = \tan \theta} \int_0^{\pi/2} \frac{\sqrt{\frac{\beta_0 a}{\sqrt{\pi}}} \frac{d\theta}{\cos^2 \theta}}{\frac{1}{\cos^2 \theta}} \notag \\ &= \frac{\pi^{3/4}}{2} \sqrt{a \beta_0} \tag{5.75} \end{align}\]が得られます。 したがって、非常に強く減衰wingg優勢になるような吸収線の等価幅は、\(\sqrt{\beta_0}\)に比例して大きくなります。 成長曲線のこの部分は減衰部(damping part)または平方根部(squareroot part)と呼ばれます。 Wing部分は、減衰定数\(a\)が大きいほど、早くに重要になります。
実際に(5.72)式を数値的に計算したものを、下図に示します。
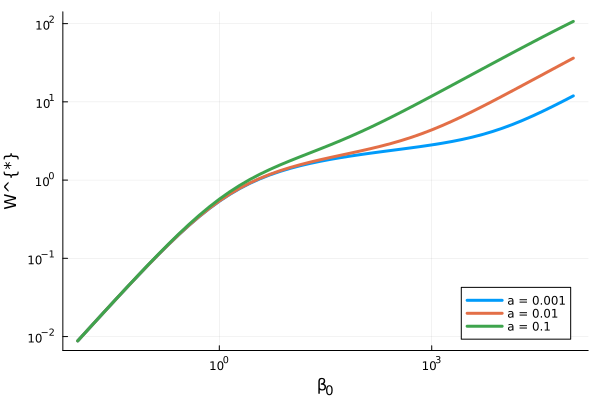
成長曲線の利用
\[\alpha_\nu = \frac{\sqrt{\pi} e^2 f}{m c \Delta \nu_d} H(a, v)\]と表されるのでした。 これを用いて、\(\beta_0\)を計算していきましょう。
\[\beta_0 = \frac{\kappa_\ell}{\kappa_c} = \frac{\kappa_\ell \rho}{\kappa_c \rho}\]ここで\(\kappa_\ell\)は、単位体積あたりの吸収線吸収係数を表します。 元素\(k\)の\(j\)番目のイオンで\(i\)番目の励起状態にある粒子が、この吸収線を作るとすると
\[\kappa_\ell \rho = \frac{\sqrt{\pi} e^2}{m c \Delta \nu_D} f n_{ijk}\]のように書くことができます。 先ほどの説明から、\(n_{ijk}\)は元素\(k\)の\(j\)番目のイオンの\(i\)番目の励起状態にある粒子数密度を表します。 さらに\(\Delta \nu_D = \xi_0 \nu_0 / c = \xi_0 / \lambda_0\)の関係より
\[\beta_0 = \frac{\sqrt{\pi} e^2}{m c} f_{ijk} \lambda_0 \frac{n_{ijk}}{\xi_0 \kappa_c \rho} \tag{5.76}\]のように表されます。 そして途中、振動子強度を\(f \rightarrow f_{ijk}\)のように、それぞれの元素やエネルギー準位ごとに異なる値を取るものとしました。
ボルツマンの関係式
を用いることで
\[n_{ijk} = \frac{N_{jk} g_{ijk}}{U_{jk} (T)} e^{-\chi_{ijk} / (k_B T)} \tag{5.78}\]のように表すことができます。 ここで\(g_{ijk}\)は元素\(k\)の\(j\)のイオンの\(i\)番目の励起状態にある粒子の統計的重率、\(U_{jk}(T)\)は分配関数、\(\chi_{ijk}\)は状態\(i\)の励起エネルギーを表します。 この関係を用いると(5.76)式は
\[\beta_0 = \frac{\sqrt{\pi} e^2}{mc} f_{ijk} g_{ijk} \lambda_0 \frac{N_{jk}}{U_{jk} \kappa_c \rho \xi_0} e^{-\chi_{ijk} / (k_B T)} \ \Longrightarrow \ \log \beta_0 = \log_{10} (f_{ijk} g_{ijk} \lambda_0) - \frac{\chi_{ijk}}{k_B T} \log_{10} e + \log_{10} C_{jk}\]のようになります。 ここで\(C_{jk} = \frac{\sqrt{\pi} e^2}{mc} \frac{N_{jk}}{U_{jk} \kappa_c \rho \xi_0}\)です。 そして\(\frac{\log_{10}e (1 \mathrm{eV})}{k_B} = 5040\)を用い、\(\theta \equiv 5040 / T\)と、\(\chi_{ijk}\)をeV単位で表すことにすると
\[\log_{10} \beta_0 = \log_{10} (f_{ijk} g_{ijk} \lambda_0) - \theta \chi_{ijk} + \log_{10} C_{jk} \tag{5.78}\]のようになります。
観測的な成長曲線の縦軸には\(\log(W_\lambda / \lambda)\)を取り、横軸には\(\log (f_{ijk} g_{ijk} \lambda) - \theta \chi_{ijk}\)を取ります。 温度\(\theta\)のある値を過程し、あるイオン(\(k\)元素の\(j\)番目のイオン; 例えばFeIIなど)が種々の励起状態\(i\)からの遷移によって、吸収線を形作るとしましょう。 この吸収線に対する等価幅を描画し、それらが単一の曲線上に乗るように、仮定する温度を調整します。 このようにして仮定される温度は励起温度(excitation temperature)と呼ばれます。
このようにして得られた観測的な成長曲線は、理論的に得られた成長曲線に対して、横軸・縦軸をズラすことでフィッティングを行います。 この操作を通して、恒星大気に対して種々の量を得ることができます。
微小な乱流 (microturbulence)
観測的な成長曲線の縦軸が\(\log (W_\lambda/ \lambda)\)であるのに対し、理論的な成長曲線は
\[\log \left( \frac{W_\nu}{\Delta \nu_D}\right) = \log \left( \frac{W_\nu}{\nu} \frac{\nu}{\Delta \nu_D} \right) = \log \left( \frac{W_\lambda}{\lambda} \right) - \log \left( \frac{\xi_0}{c}\right) \tag{5.80}\]のように書かれることから、縦軸をズラして合わせることで、\(\xi_0\)を得ることができます。 これは元々、吸収線を形成するガス粒子の視線速度を表すものでした。 よって、ガス粒子の微視的な運動の情報を得ることができたことになります。 これに対応する速度は、励起温度\(T_\mathrm{exc}\)に対応する熱運動速度
\[\xi_\mathrm{therm} = \sqrt{\frac{2k_B T_\mathrm{exc}}{A m_\mathrm{H}}} \tag{5.81}\]です。 ここで\(A\)は質量数を表します。 ところが、成長曲線から得られる\(\xi_0\)は、通常\(\xi_\mathrm{therm}\)を大きく上回ることが知られています。 そのため、非熱的な微視的運動として、微小な乱流 (microturbulence) を導入します。 この運動は、光子の平均自由行程よりも短いスケールで起こり、その速度は典型的な速度\(\xi_\mathrm{turb}\)の周りにガウス分布をすると仮定します。 このとき
\[\xi_0^2 = \frac{2k_B T_\mathrm{exc}}{A m_\mathrm{H}} + \xi_\mathrm{turb}^2 \tag{5.82}\]の関係にあります。 \(\xi_\mathrm{turb} \sim 1-2 \mathrm{km \ s^{-1}}\)が良く用いられる値のようです。
元素の組成
観測的成長曲線と理論的成長曲線の横軸を合わせることにより
\[\log C_[jk] = \log \beta_0 - [\log (f_{ijk} g_{ijk} \lambda_0) - \theta_\mathrm{exc} \chi_{ijk}] \tag{5.83}\]が得られます。 ここで、電子の数密度\(n_e\)が恒星大気のモデル計算から得られているとしましょう。 ここから連続吸収係数\(\kappa_c\)が得られます。 すると\(C_{jk}\)の定義から、\(N_{jk}\) (元素\(k\)の\(j\)回電離したイオンの数密度)が計算できます。 さらにサハの電離式を用いると、\(j\)回電離したイオンの割合を計算することができるので、\(N_k\)を得ることができます。 正確には、\(\rho \kappa_c\)が水素数密度\(N_\mathrm{H}\)に比例するため、\(N_k\)自体ではなく\(N_k / N_\mathrm{H}\)が計算されます。
ここまでの成長曲線の解析では、スペクトル線が単一の層で形成されているという簡単化をしています。 そのため、得られた元素組成は正確に反映しているとは言えません。 恒星大気モデルを用いれば、各層での各波長に対する吸収係数を計算することができ、各層の各波長に対する光学的厚みを計算することができます。 よってLTEの仮定のもとでは
によって恒星表面から出てくるフラックス、すなわちスペクトル線輪郭を得ることができます。 それとは別に観測されたスペクトル線とを直接比較することで、先程の議論から種々の量を推定することができます。 また、種々の組成に対して理論的に得られたスペクトル線輪郭から等価幅を計算し、それと観測された等価幅を比較することによって、元素組成を推定することが可能です。
太陽表面の元素組成
これまでの太陽のスペクトル線の解析により、太陽表面の詳細な元素組成が得られています。 太陽表面の元素組成(solar abundance)は、太陽系が生まれた当時の元素組成をほぼ反映していると考えられ、銀河の種族Iの恒星の標準的な元素組成と考えられています。
ただし、リチウムだけは例外です。
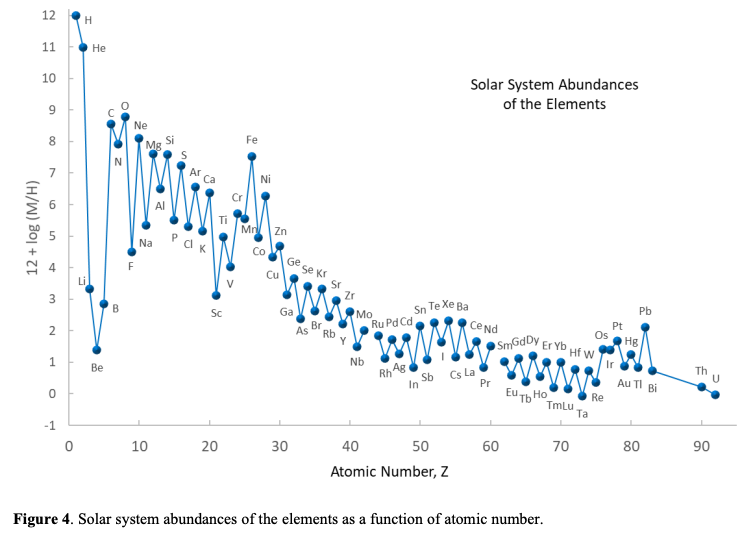
最も多く存在するのが水素(質量含有量~0.7)で、次に多いのがヘリウム(質量含有量~0.28)です。 ヘリウムの次の原子番号を持つリチウム(Li)、ベリリウム(Be)、ホウ素(B)の含有量は極端に少なく、元素含有量の原子番号分布に深い谷を形成しています。 ヘリウムからベリリウムまでの原子核の多くは、宇宙創世直後に合成されたと考えられており、これをビッグバン核合成(Big Bang nucleosynthesis)と呼びます。 それよりも重い原子核は、恒星内部や超新星爆発、そして中性子星連星合体時に合成されました。 炭素以降は、大雑把には原子番号が大きくなるにつれて含有量が少なくなります。 この傾向から大きく逸脱して、最も安定した原子核である鉄のグループが、含有量のピーク(iron-peak)を形成します。 鉄のグループよりも重たい原子核は、鉄の原子核に中性子が捕獲されて生成されたと考えられています。
恒星表面のリチウム含有量
リチウム原子核は、比較的壊れやすい原子核です。 そのため、種々の恒星表面でのリチウム含有量は、恒星内部の構造についての有益な情報を持っていると考えられています。 下図上パネルは、色々な鉄の含有量を持つ恒星の表面リチウム含有量を表したものです。 非常に重元素(ここでは鉄)の少ない恒星であっても、リチウムが生成されたことを表しており、これはビッグバン核合成を反映しているものと思われます。 リチウム含有量にヘリウム・重水素含有量を合わせることで、宇宙に存在するバリオン量を決定します。
また、太陽表面のリチウム含有量は、隕石から得られた値に比べて100分の1程度であることが知られています。 太陽系の隕石と太陽は同じ分子雲から形成されたため、太陽も誕生当初は隕石と同じリチウム含有量を持っていたはずです。 隕石のリチウム含有量との大きな違いは、太陽が46億年前に形成されて以降、何かの原因により太陽外層部にあったリチウムが壊されてしまったことを表しています。
温度が約200万度以上では、リチウムは水素原子核(陽子)を捕獲して
という反応を起こしてヘリウムとなります。 この事実に基づくならば、太陽の外層部にある物質は一度は約200万度の高温にさらされたことを表しています。 太陽外層の対流層の底の温度は約100万度と考えられているため、物質はそれよりも内側まで混合されている必要があります。 しかし、この混合のメカニズムはいまだによくわかっていません。
次の図の上パネルと下パネルはそれぞれ、ヒアデス星団(年齢約7億歳)とプレアデス星団(年齢約1億歳)中の主系列星の表面でのリチウム含有量を、恒星の有効温度(右に行くほど温度が低い)に対して描画したものです。 まずはヒアデス星団に着目しましょう。

ここに星団内の恒星は同じ分子雲から生まれたものなので、誕生当初は皆同じリチウム含有量を持っていたはずです。 しかし、約7億年が経過した現在では、この図のように恒星の質量(有効温度)によって異なる値を持ちます。
スペクトルがF6型よりも低温(小質量)の星では、表面のリチウム含有量が有効温度(質量)の減少とともに減少しています。 このような低温の主系列星の外層には対流層が存在し、その層の厚さは表面温度が減少するほど厚く、その底の温度も高くなります。 そのため表面温度の低い星ほど、対流層内をガスが循環する間に多くのリチウムが壊されると理解できます。
ヒアデス星団の主系列星の表面リチウム含有量分布のもう一つの顕著な特徴は、有効温度6700度あたりを中心に、リチウム含有量が非常に少なくなっていることです。 この程度の有効温度を持つ恒星の外層に存在する対流層は、非常に薄く外層が比較的静かな状態にあると考えられています。 このため、水素よりも重いリチウムは次第に沈んでいき、表面での含有量が小さくなります。 しかし、表面温度がそれよりも少し高い星では放射による力が強くなり、重さの違いによるリチウムの沈降を抑えるとされています。 このような理由から、6700度あたりでだけリチウム含有量が小さくなっていると理解されています。 下パネルのプレアデス星団は年齢が若いため、リチウムの沈降が進んでいないと考えられます。
補遺
(5.56)式の図示
散乱によって形成される吸収線のresidual flux (5.56)式を描画したのが下図です。 ここでは、\(\beta_\nu = \sigma_\nu / \kappa_c = \beta_0 H(a, v)\)であることから、フォークト関数を計算し、\(\beta_0 = 1, 10, 10^2, 10^3, 10^4\)、そして\(B_1 / B_0 = 1, 2, 3\)、さらに\(a = 10^{-3}\)を仮定したものを作成しました。 また計算に際して、以下のような式変形を行いました。
\[R_\nu = \frac{\sqrt{\frac{3}{1+\beta_\nu}} + \frac{B_1}{B_0}\frac{1}{1+\beta_\nu}}{\sqrt{\frac{3}{1+\beta_\nu}} + \frac{3}{2}} \frac{\sqrt{3} + \frac{3}{2}}{\frac{B_1}{B_0} + \sqrt{3}}\]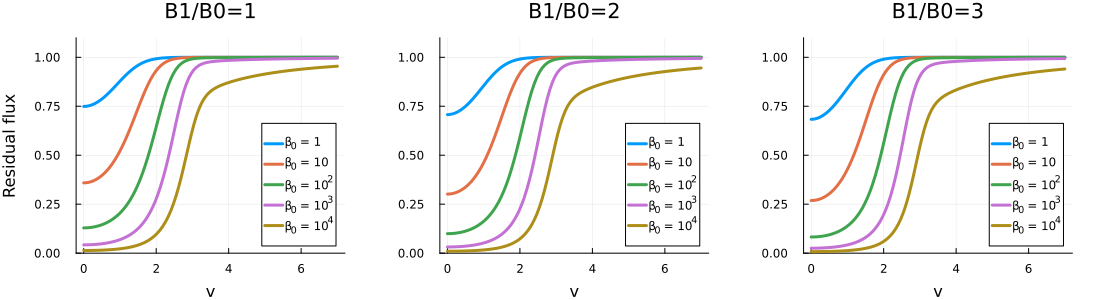
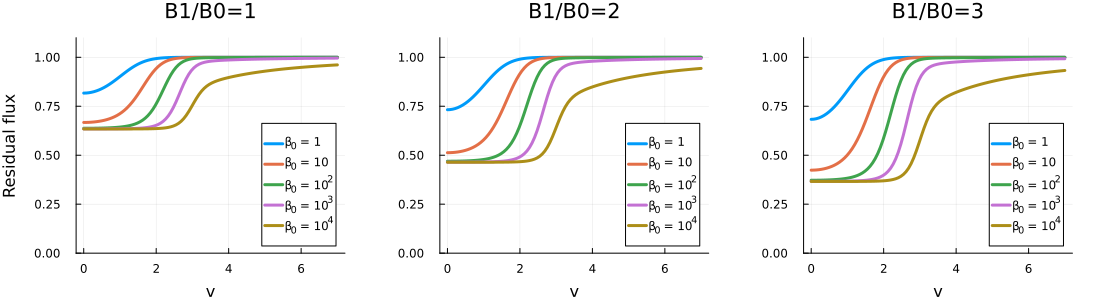
(5.57)式の図示
次の図は、吸収過程のみによって形成される吸収線のresidual flux (5.57)式を描画したものです。 先程と同様に
\[R_\nu = \frac{\sqrt{3} + \frac{1}{1+\beta_\nu} \frac{B_1}{B_0}}{\frac{B_1}{B_0} + \sqrt{3}}\]のように式変形をしました。 また、ここでは\(\beta_\nu = \kappa_\nu / \kappa_c = \beta_0 H(a, v)\)、そして\(\beta_0 = 1, 10, 10^2, 10^3, 10^4\)、そして\(B_1 / B_0 = 1, 2, 3\)、さらに\(a = 10^{-3}\)を仮定したものを作成しました。
以下は、(5.56)式を図示するために作成したJuliaスクリプトです。 これの数式を書き換えれば、(5.57)式も描くことができます。
using QuadGK
using Plots
gr()
# define the integrand funciton for Voigt function
function f(a, v, x)
return exp(-(a*x+x^2/4)) * cos(v*x)
end
# define a function for computing residual flux
function residual_flux(beta, bratio)
one_onebeta = 1 / (1+beta)
sqrt_part = sqrt(3*one_onebeta)
return (sqrt_part+bratio*one_onebeta) / (sqrt_part+1.5) * (sqrt(3)+1.5) / (bratio+sqrt(3))
end
# set array for beta0
array_beta0 = [10^0, 10^1, 10^2, 10^3, 10^4]
# get length of beta0
len_beta0 = length(array_beta0)
# set array for B1/B0
array_bratio = [1.0, 2.0, 3.0]
# get length of bratio
len_bratio = length(array_bratio)
# set a
a = 10^(-3)
# set length of v
len_v = 100
# set array for v
array_v = range(0.0, 7.0, length=len_v)
# initialize an array for residual flux
residual = zeros(Float64, len_bratio, len_beta0, len_v)
for i in 1:len_bratio
for j in 1:len_beta0
beta0 = array_beta0[j]
for k in 1:len_v
v = array_v[k]
# compute integration using quadgk
integral, error = quadgk(x -> f(a, v, x), 0, 100)
# put the integration result into voigt array
voigt = integral/sqrt(pi)
beta = beta0 * voigt
bratio = array_bratio[i]
residual[i, j, k] = residual_flux(beta, bratio)
end
end
end
# visualize residual flux
plt1 = plot(array_v, residual[1, 1, :], linewidth=3, xlabel="v", ylabel="Residual flux", label=raw"\beta_{0} = 1", ylim=(0.0, 1.1), title="B1/B0=1", margin=Plots.Measures.Length(:mm, 5.0))
plot!(array_v, residual[1, 2, :], linewidth=3, label=raw"\beta_{0} = 10")
plot!(array_v, residual[1, 3, :], linewidth=3, label=raw"\beta_{0} = 10^{2}")
plot!(array_v, residual[1, 4, :], linewidth=3, label=raw"\beta_{0} = 10^{3}")
plot!(array_v, residual[1, 5, :], linewidth=3, label=raw"\beta_{0} = 10^{4}")
plt2 = plot(array_v, residual[2, 1, :], linewidth=3, xlabel="v", label=raw"\beta_{0} = 1", ylim=(0.0, 1.1), title="B1/B0=2", margin=Plots.Measures.Length(:mm, 5.0))
plot!(array_v, residual[2, 2, :], linewidth=3, label=raw"\beta_{0} = 10")
plot!(array_v, residual[2, 3, :], linewidth=3, label=raw"\beta_{0} = 10^{2}")
plot!(array_v, residual[2, 4, :], linewidth=3, label=raw"\beta_{0} = 10^{3}")
plot!(array_v, residual[2, 5, :], linewidth=3, label=raw"\beta_{0} = 10^{4}")
plt3 = plot(array_v, residual[3, 1, :], linewidth=3, xlabel="v", label=raw"\beta_{0} = 1", ylim=(0.0, 1.1), title="B1/B0=3", margin=Plots.Measures.Length(:mm, 5.0))
plot!(array_v, residual[3, 2, :], linewidth=3, label=raw"\beta_{0} = 10")
plot!(array_v, residual[3, 3, :], linewidth=3, label=raw"\beta_{0} = 10^{2}")
plot!(array_v, residual[3, 4, :], linewidth=3, label=raw"\beta_{0} = 10^{3}")
plot!(array_v, residual[3, 5, :], linewidth=3, label=raw"\beta_{0} = 10^{4}")
plt = plot(plt1, plt2, plt3, layout=(1, 3), size=(1100, 300))
savefig(plt, "spectral_line_formation_05.png")
参考文献
[1] Lodders, 2019, “Solar Elemental Abundances”
[2] Lyubimkov, 2016, “Lithium in Stellar Atmospheres: Observations and Theory”
[3] 野本憲一, 定金晃三, 佐藤勝彦, “シリーズ現代の天文学, 恒星”
[4] 桜井隆, 小島正宜, 小杉健郎, 柴田一成, “シリーズ現代の天文学, 太陽”