遷移放射
問題設定
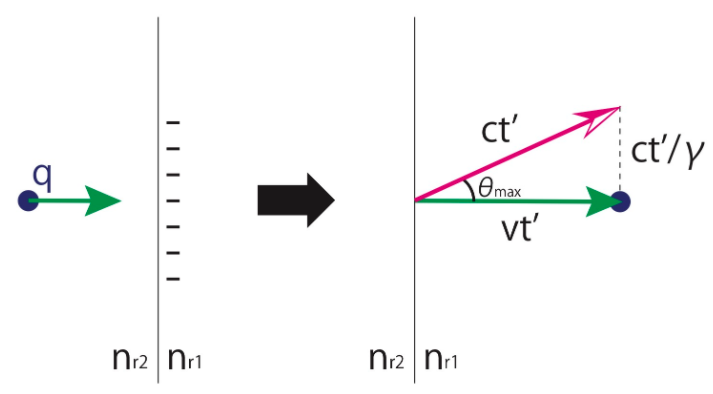
屈折率\(n_{r1}\)の一様媒質中と屈折率\(n_{r2}\)の一様媒質中が\(z=0\)面を挟んで隣り合っています。そこに電荷\(q\)の荷電粒子が\(z\)軸に沿って等速直線運動で通り過ぎるときに発生する電磁放射を考えましょう。荷電粒子は\(z=L/2\)から出発し、\(t'=0\)で境界面に達するものとします。簡単のため、\(n_{r1}=1\)(真空)、\(n_{r2}=\infty\)(完全導体)と考えましょう。
電磁気学を思い出すと、このときに荷電粒子が作る電場は胸像法によって求めることができるのでした。具体的には、荷電粒子とは反対の電荷\(-q\)をもつ擬似粒子が\(z=-L/2\)から出発し、同様に等速直線運動で導体表面まで運動を行います。導体表面で荷電粒子と擬似粒子は衝突し、電荷のない中性状態に落ち着くとします。 軸対称性より、観測者は\(yz\)平面内にいるとし、また十分遠方にいる(\(R \gg L\))と仮定します。
フーリエスペクトル
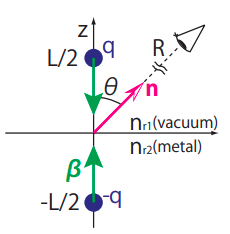
観測者の方向を向いた単位ベクトルは
\[{\bf n} = (0, \sin \theta, \cos \theta)\]荷電粒子の位置ベクトルと速度ベクトルはそれぞれ
\[{\bf r}_{0, q} (t') = (0, 0, -vt')\] \[\boldsymbol{\beta}_{q} = -(0, 0, \beta) = -(0, 0, \frac{v}{c})\]などです。また、擬似粒子の位置ベクトルと速度ベクトルはそれぞれ
\[{\bf r}_{0, -q} (t') = (0, 0, vt') =-{\bf r}_{0, q}\] \[\boldsymbol{\beta}_{-q} = (0, 0, \beta) = (0, 0, \frac{v}{c}) =-\boldsymbol{\beta}_{q}\]などです。では具体的な計算をしていきましょう。観測時間が十分長く、長時間平均をとるとすると輻射場のフーリエスペクトルは、荷電粒子の作る電場と擬似粒子の作る電場の重ね合わせより
\[\begin{aligned} {\hat {\bf E}}({\bf r}, \omega) &= - \frac{i \omega q}{2\pi cR} e^{i\omega \frac{\mathbf{n} \cdot \mathbf{r}}{c}} \int_{T'_1}^{T'_2} \mathbf{n} \times (\mathbf{n} \times \boldsymbol{\beta}_{q})e^{i \omega (t'-\frac{\mathbf{r}_{0, q}(t') \cdot \mathbf{n}}{c})} dt'- \frac{i \omega (-q)}{2\pi cR} e^{i\omega \frac{\mathbf{n} \cdot \mathbf{r}}{c}} \int_{T'_1}^{T'_2} \mathbf{n} \times (\mathbf{n} \times \boldsymbol{\beta}_{-q})e^{i \omega (t'-\frac{\mathbf{r}_{0, -q}(t') \cdot \mathbf{n}}{c})} dt' \\ &= \frac{i \omega q}{2\pi cR} e^{i\omega \frac{\mathbf{n} \cdot \mathbf{r}}{c}} \mathbf{n} \times (\mathbf{n} \times \boldsymbol{\beta}_{-q})\int_{T'_1}^{T'_2} \left\{ e^{i \omega (t'+\frac{\mathbf{r}_{0, -q}(t') \cdot \mathbf{n}}{c})}+ e^{i \omega (t'-\frac{\mathbf{r}_{0, -q}(t') \cdot \mathbf{n}}{c})} \right\} dt' \end{aligned}\]今後の計算に必要なものを計算しておきましょう。
\[{\bf n} \times ({\bf n} \times \boldsymbol{\beta}_{-q}) = ({\bf n} \cdot \boldsymbol{\beta}_{-q}) {\bf n} - \boldsymbol{\beta}_{-q} = \beta \cos \theta \left( \begin{array}{c} 0 \\ \sin \theta \\ \cos \theta \end{array} \right) - \beta \left( \begin{array}{c} 0 \\ 0 \\ 1 \end{array} \right) =\beta \left( \begin{array}{c} 0 \\ \sin \theta \cos \theta \\ -\sin^2 \theta \end{array} \right)\] \[t'+\frac{\mathbf{r}_{0, -q} \cdot \mathbf{n}}{c} = t' + \frac{v}{c} t' \cos \theta =(1+ \beta \cos \theta )t'\] \[t'-\frac{\mathbf{r}_{0, -q} \cdot \mathbf{n}}{c} = t' - \frac{v}{c} t' \cos \theta =(1- \beta \cos \theta )t'\]また、問題設定より\(T_1'=-L/(2v), T_2'=0\)です。それでは各成分の計算を行います。
\[{\hat E}_x =0\] \[\begin{aligned} {\hat E}_y (\mathbf{r} , \omega) &= \frac{i \omega q}{2\pi c R} \beta \sin \theta \cos \theta e^{i\omega \frac{\mathbf{n} \cdot \mathbf{r}}{c}} \int_{-L/(2v)}^0 \left\{ e^{i\omega (1+ \beta \cos \theta) t'}+e^{i\omega (1- \beta \cos \theta) t'} \right\} dt' \\ &=\frac{i \omega q}{2\pi c R} \beta \sin \theta \cos \theta e^{i\omega \frac{\mathbf{n} \cdot \mathbf{r}}{c}} \left\{ \frac{1-e^{-i\omega (1+ \beta \cos \theta) L/(2v)}}{i \omega (1+\beta \cos \theta)}+ \frac{1-e^{-i\omega (1- \beta \cos \theta) L/(2v)}}{i \omega (1-\beta \cos \theta)}\right\} \end{aligned}\]ここで\(\omega L /v=\omega/c \cdot L/\beta\)と書きます。\(\omega/c\)は観測する電磁波の波数です。粒子の走る距離\(L\)が十分長ければ、\(\omega L /c \gg 1\)となります。よって振動項は激しく振動し、観測者はこの平均を見ているとして、この項を0として扱ってよいでしょう。
\[\therefore \ {\hat E}_y ({\bf r} , \omega) =\frac{i \omega q}{2\pi c R} \beta \sin \theta \cos \theta e^{i\omega \frac{\mathbf{n} \cdot \mathbf{r}}{c}} \left\{ \frac{1}{i \omega (1+\beta \cos \theta)}+ \frac{1}{i \omega (1-\beta \cos \theta)}\right\} =\frac{q}{\pi c R} \frac{\beta \sin \theta \cos \theta}{1-\beta^2 \cos^2 \theta} e^{i\omega \frac{\mathbf{n} \cdot \mathbf{r}}{c}}\]\(\hat{E}_y\)と\(\hat{E}_z\)の違いは\(\sin \theta \cos \theta\)と\(-\sin^2 \theta\)の違いのみなので
\[\hat{E}_z (\mathbf{r} , \omega) =\frac{q}{\pi c R} \frac{-\beta \sin^2 \theta}{1-\beta^2 \cos^2 \theta} e^{i\omega \frac{\mathbf{n} \cdot \mathbf{r}}{c}}\]放射強度
単位周波数、単位立体角あたりの放射強度を求めましょう。
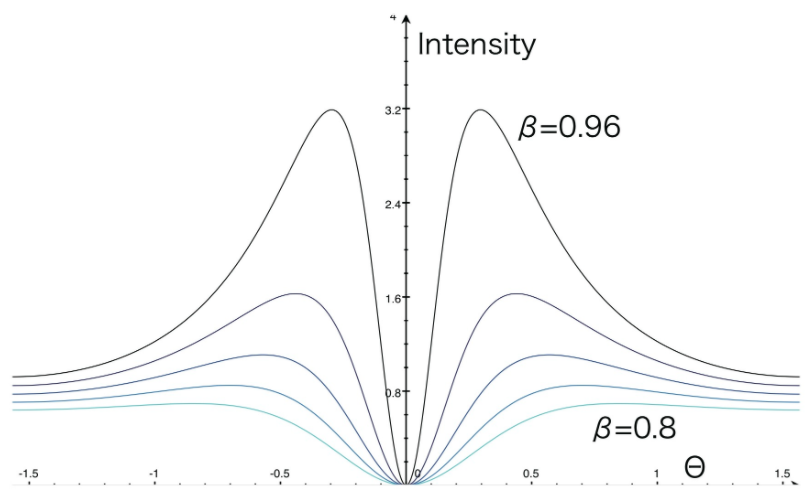
\[\frac{dW}{d\omega d\Omega} = cR^2 (|{\hat E_x}|^2+|{\hat E_y}|^2+|{\hat E_z}|^2) =\frac{q^2}{\pi^2c}\frac{\beta^2(\sin^2 \theta \cos^2 \theta+ \sin^4 \theta)}{(1-\beta^2 \cos^2 \theta)^2} =\frac{q^2}{\pi^2c}\frac{\beta^2 \sin^2 \theta}{(1-\beta^2 \cos^2 \theta)^2} \tag{1}\]この式の角度依存性は下図のようになります。また、粒子の速度が光速度に近づくにつれて放射強度も大きくなっていることがわかります。この式はソビエト連邦(現ロシア)の物理学者Vitaly GinzburgとIlya Frankよって1946年に予言されました。その名にちなんで、Ginzburg-Frank formula(ギンツブルグ・フランクの式)と呼ばれています。1959年にこの現象は発見され、理論の正当性が示されました。現在ではこの原理は高エネルギー粒子の観測装置として用いられており、これを用いた検出器をTRD(Transition Radiation Detector)と呼びます。
放射強度が最大となる角度
放射強度が最大となる角度を求めてみましょう。そのためには\(\alpha=\sin^2 \theta\)とおいて微分を行います。
\[\begin{aligned} &\frac{d}{d\alpha} \frac{\beta^2 \alpha}{\left\{1-\beta^2(1-\alpha) \right\}^2} =\frac{\beta^2 (1-\beta^2 + \beta^2 \alpha)^2-2 \beta^2 \alpha(1-\beta^2 + \beta^2 \alpha )\beta^2}{(1-\beta^2+ \beta^2 \alpha)^4} =0 \ \Longrightarrow \ 1-\beta^2 -\beta^2 \alpha =0 \\ &\Longrightarrow \ \alpha = \sin^2 \theta_{\rm max} = \frac{1-\beta^2}{\beta^2} =\frac{1}{\gamma^2 \beta^2} \end{aligned}\] \[\therefore \ \sin \theta_{\rm max} = \frac{1}{\gamma \beta} \ \Longrightarrow \ \theta_{\rm max} = \sin^{-1} \left( \frac{1}{\gamma \beta} \right) \simeq \frac{1}{\gamma} \ ({\rm for} \ \gamma \gg 1)\]放射角が小さいとき
荷電粒子の速度が光速度に近づくほどに、放射角度は小さくなっていくことがわかります。このことから、\(\sin^2 \theta \simeq \theta^2, \cos^2 \theta \simeq 1- \theta^2\)と近似すると
\[\begin{aligned} \frac{dW}{d\omega d\Omega} &\simeq \frac{q^2}{\pi^2c}\frac{\beta^2 \theta^2}{\left\{ 1-\beta^2 (1-\theta^2) \right\}^2} = \frac{q^2}{\pi^2c}\frac{\left( 1- 1/\gamma^2 \right)\theta^2}{\left\{ 1-(1-1/\gamma^2)(1-\theta^2) \right\}^2} =\frac{q^2}{\pi^2c}\frac{\gamma^2 \left( \gamma^2- 1\right)\theta^2}{\left\{ \gamma^2-(\gamma^2-1)(1-\theta^2) \right\}^2} \\ &= \frac{q^2}{\pi^2c}\gamma^2 \frac{\gamma^2 \theta^2- \theta^2}{( 1+\gamma^2 \theta^2 -\theta^2 )^2} \underbrace{\simeq}_{\theta \ll 1} \frac{q^2}{\pi^2c}\gamma^2 \frac{\gamma^2 \theta^2}{( 1+\gamma^2 \theta^2 )^2} \end{aligned}\]という簡単な形に表現することができます。
図による解釈
遷移放射の原理は以下のように説明できます。電荷を持った粒子が導体表面に近づくと、境界面で分極が生じます。荷電粒子が通り過ぎるとその分極は元に戻ろうとします。その時に放射が生じるのです。次の右図のような直角三角形を考えましょう。点線で示された線分の長さは\(\sqrt{(ct')^2-(vt')^2}=ct'\sqrt{1-\beta^2}=ct'/\gamma\)で与えられます。これは放射角が\(\theta_{\rm max}\)式となっていることと見事に一致していることがわかります。