Table of contents
ガン・ピーターソンテスト (Gunn-Peterson test)
高赤方偏移宇宙において宇宙空間にどのくらい中性水素が存在するかを確認できるメカニズムをご紹介します。
光学的厚さ
3次元的な距離を\(\ell\)とすると、この距離は固有距離\(\chi\)を用いて
\[d\ell = ad\chi\]中性水素の数密度を\(n\)、また簡単に散乱断面積を\(\sigma\)とします。そしてLyαを放出している天体までの距離をQとすると、光学的厚さ\(\tau\)は
\[\tau = \int_0^Q n\sigma a d\chi = \int_0^{z_Q} n \sigma a \frac{d\chi}{dz} dz\]ここで天体の赤方偏移を\(z_Q\)としました。固有距離と赤方偏移の関係式より
\[\frac{d\chi}{dz} = \frac{c}{H}\]そしてさらに簡単のためにアインシュタイン・ド・ジッター宇宙を考えましょう。すると\(H = H_0 (1+z)^{3/2}\)より
\[\tau = \int_0^{z_Q} n\sigma \frac{1}{1+z} \frac{c}{H_0 (1+z)^{3/2}}dz\]大雑把な見積もりのために\(\sigma\)は赤方偏移に依存しないものと仮定します。すると保存則から
\[n = n(0) (1+z)^3\]より
\[\begin{aligned} \tau &= \frac{c \sigma n(0)}{H_0} \int_0^{z_Q} (1+z)^3 \frac{dz}{(1+z)^{5/2}} = \frac{c \sigma n(0)}{H_0} \int_0^{z_Q} (1+z)^{1/2} dz = \frac{2c \sigma n(0)}{3H_0} [(1+z)^{3/2}]_0^{z_Q} \\ &= \frac{2c \sigma n(0)}{3H_0} ((1+z_Q)^{3/2}-1) \end{aligned}\]よって遠方天体の赤方偏移\(z_Q\)が大きいとき、Lyα光子を吸収する粒子の数密度nがよほど小さくない限り、\(\tau\)はとても大きくなることがわかります。よって中性水素の比率\(\chi_{\rm HI}\)がよほど小さくない限り、必ず吸収されたスペクトルが観測されることがわかります。
観測
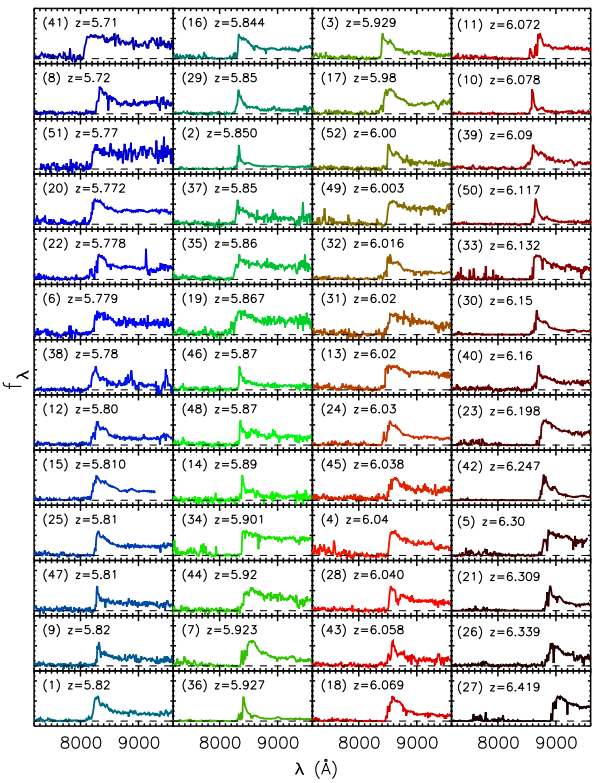
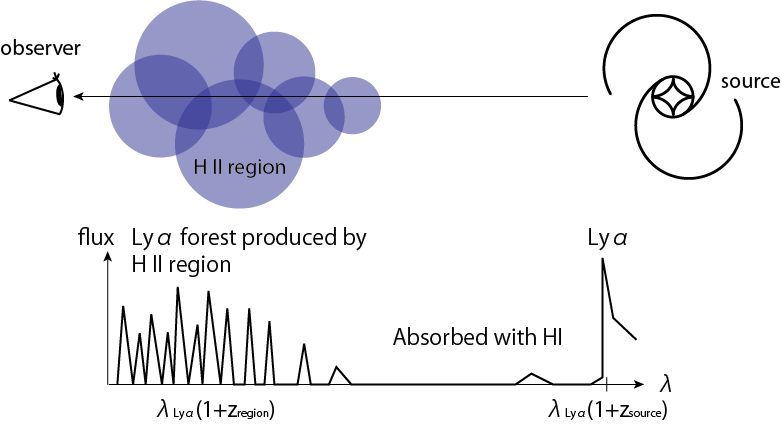
以下の図はSDSS(Sloan Digital Sky Survey)による\(z = 5.7 - 6.4\)のQSOのスペクトル観測結果です。不連続になっている部分はLyα輝線とガン・ピーターソン効果による吸収との境目です。QSOのLyαよりも短波長側が吸収されていることがわかります。これはQSOよりも我々に近い側(QSOの手前にある赤方偏移が小さい側)にある中性水素ガスによって吸収が起こるためです。
参考文献
- Jiang et al., 2016, “The Final SDSS High-Redshift Quasar Sample of 52 Quasars at z>5.7”
- Shneider, 2016, “Extragalactic Astronomy and Comology: An Introduction”