Table of contents
# 主系列星の内部構造とヘリウム燃焼までの進化
恒星の構造と進化についての大まかな議論
数値計算により得られる恒星の構造モデルを見る前に、恒星の構造を記述する微分方程式から近似的に得られる恒星の構造について、そのおおまかな特性について見ていきましょう。
最初に、静水圧平衡の式 (7.1.1)から、おおよその関係として
という関係が得られます。 また理想気体の状態方程式の関係 \(P \propto \rho T / \mu\)と、平均密度は\(\rho \propto M / R^3\)であることを組合せれば
\[P \propto MR^{-3} T / \mu \tag{8.1.2}\]の関係を得ます。 (8.1.1), (8.1.2)式を用いることで、恒星内部の温度が
\[T \propto \mu M / R \tag{8.1.3}\]のように表されます。 この式は、理想気体のもとでは恒星の内部温度は星の質量が大きいほど、また半径が小さいほど高いことを表しています。 これは質量が大きく半径が小さいほど自己重力が強く、それに対抗するために大きな圧力勾配が必要となるため、中心温度が高くなっている必要があるからと理解できます。 また質量が同じでもガスの平均分子量\(\mu\)が大きいほど温度が高いのは、平均分子量が大きいと(単位質量あたりの粒子数が少ないために)、同じ圧力を出すのにより高い温度が必要となるためです。
さらに(7.1.3)式より、輻射でエネルギーが運ばれる場合の荒い近似として
の関係が得られます。 これをさらに(8.1.3)式に用いれば
\[L \propto \frac{\mu^4 M^3}{\kappa} \tag{8.1.4}\]となります。 この式は(ガスの状態方程式がほぼ理想気体で表される場合)、恒星の光度\(L\)が静水圧平衡とエネルギー輸送により決まることを表しています。 (ただし、核融合反応によるエネルギー発生には一切触れていないことに留意しましょう。) これは静水圧平衡を保つために必然的に発生する温度勾配により、エネルギーが恒星の中心から表面に向かって流れ、それが恒星表面から放出されるのが星の光 (光度)になると理解できます。
不透明度\(\kappa\)が電子散乱で支配されているとき、つまり\(\kappa \approx 0.2 (1+X)\)であるとき、上の関係式は
のようになります。 主系列星では大質量星の内部の不透明度が電子散乱により決定されるため、大質量主系列星の光度は質量の3乗に比例することを表しています。
また不透明度がクラマース型の密度温度依存性を持つ場合
のように書けます。 この関係式を(8.1.4)式に用いれば
\[L \propto \mu^{7.5} M^{5.5} R^{-0.5} \tag{8.1.6}\]が得られます。
恒星内部での核融合反応によるエネルギー発生率が、恒星表面からのエネルギー放出率(光度)よりも大きいと恒星は膨張し、逆の場合は収縮します。 膨張または収縮による恒星の半径変化に対し、不透明度\(\kappa\)が電子散乱で支配されている大質量星では、(8.1.5)式から変化はありません。 しかし不透明度がクラマース型の中質量星の場合、(8.1.6)式より、半径が大きくなると光度が減少します。
主系列星の内部構造
主系列星段階では、核融合反応によるエネルギー発生率と光度\(L\)が釣り合っているため、恒星はその段階で半径を大きく変化させることはありません。 そして中心で水素が枯渇するまで、長時間安定な状態を保ちます。 核融合反応によるエネルギー発生率と\(L\)が等しくなっていることを用いて、主系列星の半径の質量依存性を導出してみましょう。 核融合による単位質量あたりのエネルギー発生率を
\[\epsilon_\mathrm{n} = \epsilon_0 \rho T^\nu \quad (\nu \gg 1)\]のように表しましょう。 光度と恒星全体での核融合によるエネルギー発生率が釣り合っているため
\[L = \int_0^M \epsilon_\mathrm{n} dM_r \propto M \left( \frac{M}{R^3}\right) \left( \frac{M}{R}\right)^\nu = \frac{M^{2+\nu}}{R^{3+\nu}} \simeq \frac{M^{18}}{R^{19}} \tag{8.2.1}\]の関係が得られます。 最後の部分には、代表的な値として\(\nu \sim 16\)を用いました。 ガスの不透明度が電子散乱で支配されている大質量星の場合、(8.2.1)式と(8.1.5)式より
\[M^3 \propto \frac{M^{18}}{R^{19}} \ \Longrightarrow \ R \propto M^{15/19} \simeq M^{0.8} \quad (電子散乱不透明度) \tag{8.2.2}\]となります。 またガスの不透明度がクラマース型の場合、(8.2.1), (8.1.6)式より
\[\frac{M^{5.5}}{R^{0.5}} \propto \frac{M^{18}}{R^[19]} \ \Longrightarrow \ R \propto M^{12.5/18.5} \simeq M^{0.7} \quad (クラマース型不透明度) \tag{8.2.3}\]のように表されます。 さらにこの関係を(8.1.6)式に使えば
\[L \propto M^{5.1} \quad (クラマース型不透明度)\]という、質量-光度関係を得ることができます。 次の図は、上述の議論から得られた質量-光度関係と、実際の恒星の観測を比較したものです。 連星系内に存在する恒星の質量と光度を観測から求めたものを、灰色点で表しています。 理論的に得られた実線と、良い一致を示していることがわかります。
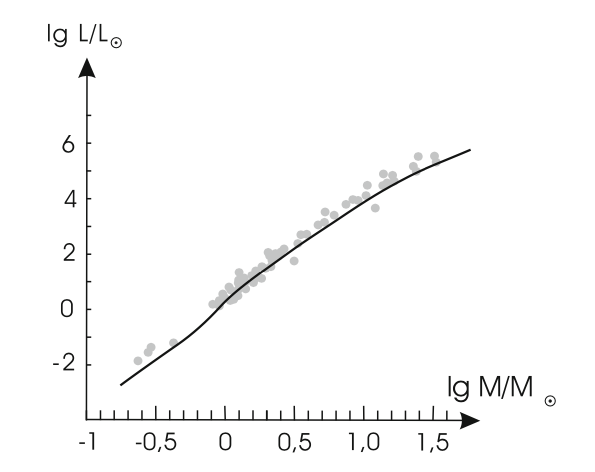
そして次の図は、\(1M_\odot\)と\(10M_\odot\)の恒星のゼロ年齢主系列段階(ZAMS)の構造を比較したものです。 この図において、\(m\)は\(M_r\)、\(l\)は\(L_r\)を表します。 aは密度分布、bは\(M_r\)と中心からの距離\(r\)の関係、cは温度分布、dは核融合反応による単位質量あたりのエネルギー発生率の分布、そしてeは\(L_r / L\)の分布を表します。
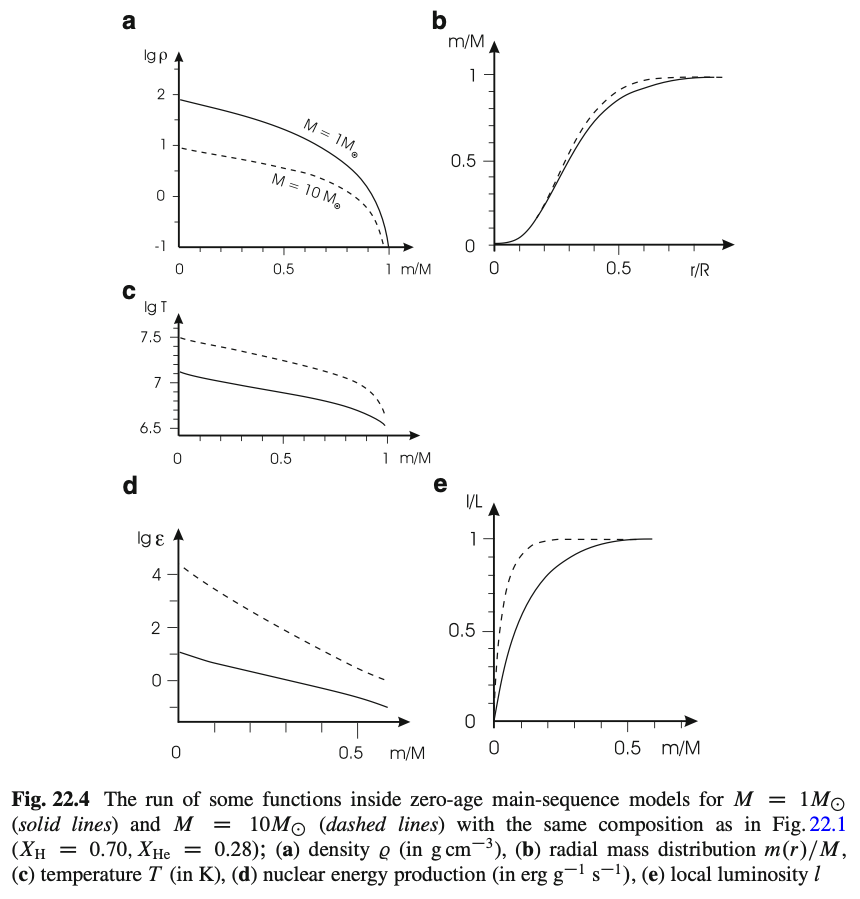
bの図から、主系列星では、中心からの距離が全体の半径の半分程度の球に質量の大半が入っていることがわかります。 aとcの図は、質量が大きい主系列星ほど平均密度が小さく、温度は高いことを表しています。 これらの性質は、(8.2.2), (8.2.3)式より
\[\bar{\rho} \propto \frac{M}{R^3} \propto M^{-1.4} \quad または \quad \bar{\rho} \propto M^{-1.1}\]が得られます。 また(8.1.3)式と組合せることで
\[T \propto M^{0.3 \sim 0.2}\]の関係が得られることから、理解できます。
水素燃焼は、\(10 M_\odot\)の恒星ではエネルギー発生率の温度依存性が大きいCNOサイクル (\(\epsilon_\mathrm{n} \propto T^{\sim 16}\))によって起こり、\(1M_\odot\)程度の星では温度依存性がさほど大きくない ppチェイン (\(\epsilon_\mathrm{n} \propto T^{\sim 4}\))で起こるため、エネルギー発生率の中心集中度は大質量星の方が大きくなります。 そのため\(10M_\odot\)の主系列星では、中心部の約10%の質量により、光度\(L\)のほとんどがまかなわれています。 それに対し、太陽質量程度の恒星では中心部の約30%の質量により作られています (eの図も合わせてご参照ください。)
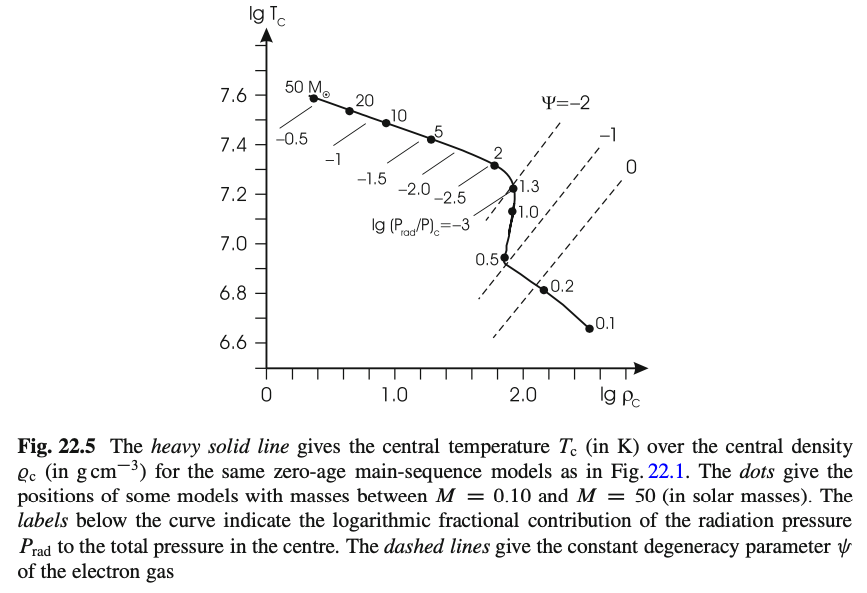
次の図は、様々な質量をもつZAMSの中心温度と中心密度を描画したものです。 この図の\(\psi\)は化学ポテンシャルを\(k_B T\)で割ったものです。 \(\psi = \eta > 0\)のとき、電子の縮退の影響が大きくなります。 太陽質量の30%より低質量の主系列星では、電子の縮退の影響が大きいことがわかります。
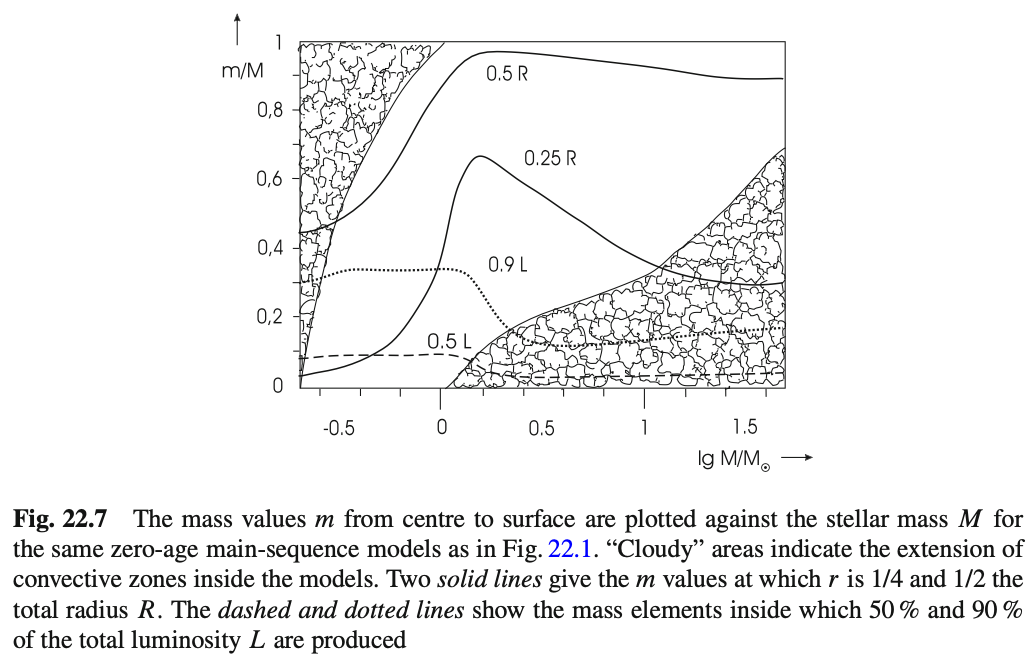
そして次の図は、横軸を恒星質量としたときに、内部の対流層の分布がどのように異なっているかを表したものです。 CNOサイクルによるエネルギー発生率は温度依存性が非常に大きいため、大・中質量星では中心に非常に近いところでほとんどのエネルギーが生成されます (下図の\(0.9L\)の場所を指す点線を参照。) そのため中心部でエネルギー流束が大きく、それを輻射だけで流すには温度勾配が急峻になりすぎるため、対流が発生しエネルギーが主に対流で運ばれるようになります。 対流の起こっている中心部(対流中心核)に含まれる質量は、恒星質量が大きくなるにつれて大きくなり、\(50 M_\odot\)ではその70%が対流中心核となります。 太陽質量程度を境に、大質量側では対流中心核と輻射エンベロープから、小質量側では輻射コアと対流エンベロープの構造に変化していることもわかります。 つまり小質量星中心部ではエネルギーは輻射で運ばれますが、外層では対流が発生していることになります。 これは小質量星の表面温度が低いことが原因です。 不透明度は、完全電離領域では温度が低いほど大きな値をもち、また温度が1万K程度で水素、数万K程度でヘリウムの電離のために大きな値を持ちます。 輻射で運ばれるエネルギー流束は温度勾配に比例し、不透明度に逆比例します。 そのため、小質量星の外層では温度勾配が急峻になり、対流が発生するのです。 対流外層の質量比は質量が小さくなるほど大きくなり、質量が\(M \lesssim 0.3 M_\odot\)の恒星では恒星全体が対流平衡となります。
主系列からヘリウム燃焼段階までの進化
次の図は、\(5M_\odot\)の恒星の主系列段階から、ヘリウム燃焼終了後までの内部構造の進化とHR図上の進化経路を表したものです。
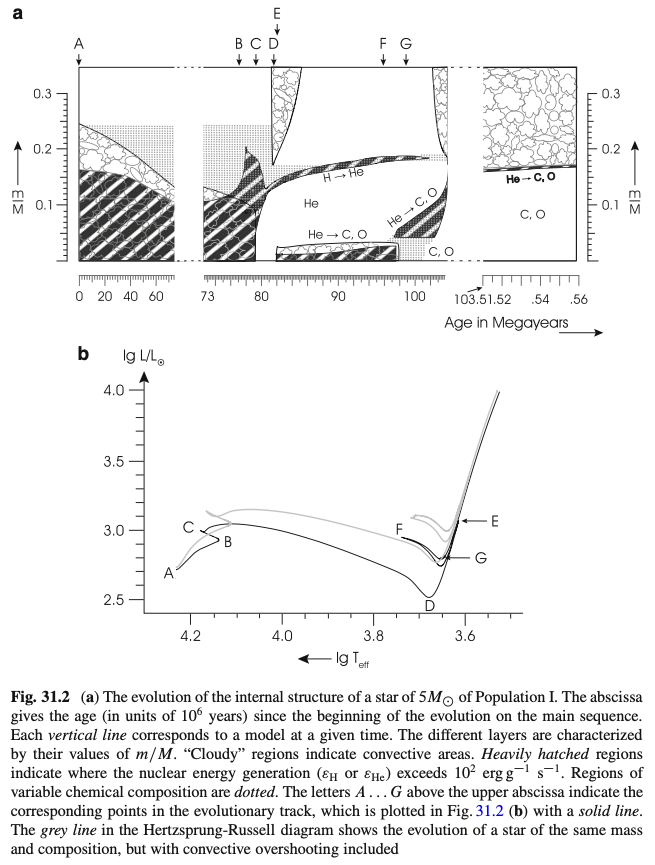
主系列進化の末期 (B点付近)に対流中心核全体で水素が枯渇し、エネルギー源がなくなるために星は重力収縮を行います。 その後(B->C)、ヘリウム中心核の周りで水素燃焼 (水素燃焼殻, hydrogen burning shell)が起こります。 中心核が重力収縮すると同時に外挿が膨張し、赤色巨星になったのち、中心でヘリウム燃焼が始まります。 主系列段階からヘリウム燃焼の始まりまでの内部の各層の半径を示したのが、次の図です。

主系列段階が終わると、速い時間スケールで中心核が収縮し、外層が膨張する様子がわかります。 外層が膨張して表面温度が下がると、次に対流外層が発達します。
次にHR図は、種々の質量をもつ中質量星の主系列段階からヘリウム燃焼終了までの進化経路を示したものです。 \(\log T_\mathrm{eff} \sim 3.8\)に斜める走る2本の直線に挟まれた領域では、外層が不安定で脈動を起こすために、セファイド不安定帯 (cepheid instability strip)と呼ばれています。 セファイド型変光星は、その不安定帯に存在しています。
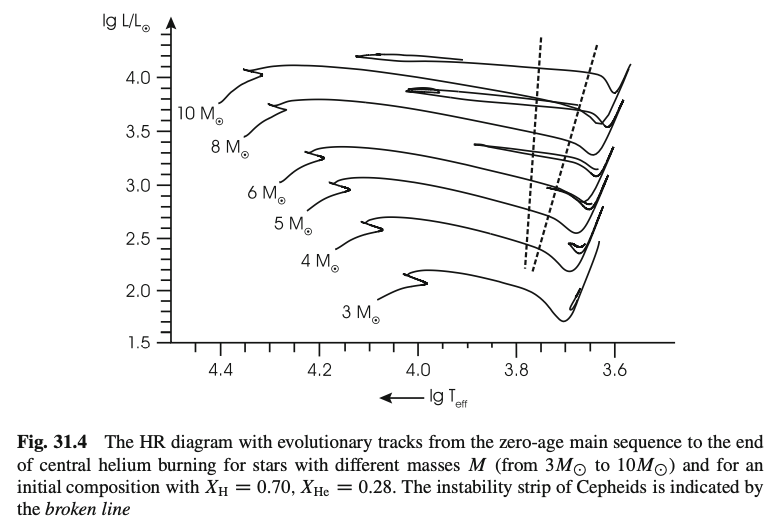
中質量星はそのヘリウム燃焼段階でHR図上でセファイドループを描き、その際にセファイド不安定帯に入り、セファイド型脈動変光星となります (主系列段階から赤色巨星に膨張する進化段階でもこの不安定帯を横切りますが、その滞在時間は短いためにほとんどのセファイドはヘリウム燃焼段階にあると考えられます。) セファイドループは恒星質量が小さいほど短く、\(M \lesssim 4M_\odot\)の星のセファイドループは、セファイド不安定帯まで届きません。
セファイド型変光星には周期-光度関係があることが知られています。 この性質は、系外銀河までの距離の決定に重要です。 以下ではこれを考えてみましょう。 星の脈動(基本脈動)周期\(\Pi\)は、自由落下時間程度なので
と表されます。 またセファイド不安定帯の幅が無視できるほど小さいとすると、その有効温度と光度の間には
\[\log L = a \log T_\mathrm{eff} + b \quad (a, bは定数)\]の関係があります。 さらに有効温度と光度、そして半径の関係
\[L = 4\pi R^2 T_\mathrm{eff}^4\]を組合せると、セファイド不安定帯内の星の半径が、光度\(L\)だけの関数として書けます。 さらにセファイドループの光度は質量が大きいほど大きいという、\(M\)と\(L\)との間の一対一の関係があります。 これらを(8.3.1)式に入れることで、周期\(\Pi\)と光度\(L\)の間の一対一関係、周期-光度関係 (period-luminosity relation)が存在することがわかります。
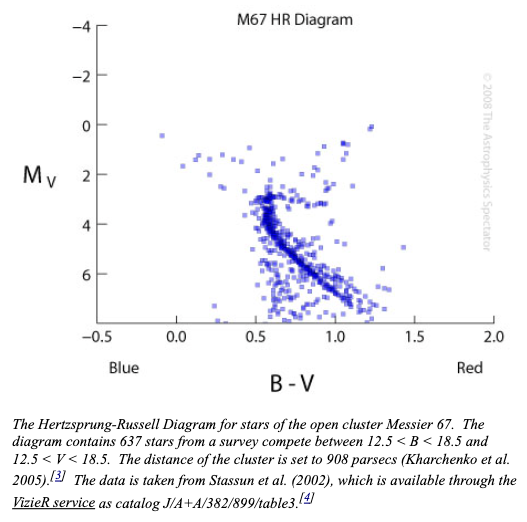
次の図は、古い散開星団であるM67 (年齢はおよそ50億年)のHR図を表しています。 この星団のうち、主系列を離れようとしている恒星の質量は\(\sim 1.2 M_\odot\)とされています。 このような低質量星では主系列を終了し、ヘリウム中心核が出来ても、すぐに中心核の収縮は起こらずにHR図上の主系列星のそばにしばらく留まることが知られています。 これはHR図上で主系列の終端部分よりも明るい部分(図の左上部分)にも、星が存在することに対応しています。
主系列そしてヘリウム燃焼段階の寿命は、\(M / L\)に比例します。 一般に\(L \propto M^{3 \sim 4}\)なので、寿命\(\tau\)は
\[\tau \propto M^{-2 \sim -3}\]のようになり、質量が大きいほど短くなります。 しかし恒星質量が非常に大きくなると、平均密度が小さくなります。 すると、輻射圧がガス圧に比べて大きくなり、\(L \propto M\)のようになります (詳細な計算はこちらをご覧ください。) そのため、非常に質量の大きい恒星での寿命は、質量に依存せずに一定となります。
参考文献
[1] Kippenhahn, Weigert & Weiss, “Stellar Structure and Evolution”
[2] The Astrophysics Spectator, “The Hertzsprung-Russell Diagrams of Star Clusters”
[3] 高原文郎, “宇宙物理学”
[4] 野本憲一, 定金晃三, 佐藤勝彦, “恒星”