Table of contents

1次のフェルミ加速 (1st order Fermi acceleration)

1次のフェルミ加速 (1st order Fermi acceleration)

ここでは高エネルギー宇宙線の加速機構として知られる、衝撃波でのフェルミ加速 (1次のフェルミ加速)についてメモします。

衝撃波におけるフェルミ加速

以下では、簡単のためテスト粒子近似を用い、フェルミ加速の原理を見ていきましょう。テスト粒子近似では、熱的な粒子からなるマクロなプラズマ流は、衝撃波のランキン-ユゴニオ関係を満たすように与えられるとします。その流れの中での非熱的な高エネルギー粒子の運動について考えるのですが、この粒子の存在によって流れが乱されるようなことはないものとします。さらにここで考える衝撃波は、その波面が磁場に垂直である(平行衝撃波)とします。
一般にプラズマ中には磁場の乱れ (主としてアルヴェーン波と呼ばれる横波)が存在しています。この磁場の乱れによって、荷電粒子はその軌道のピッチ角を変化させ、ついには進行方向を変えることになります。上流と下流の流体速度よりも大きな速度を持つ荷電粒子は、波によって散乱され、その運動方向を変えます。これにより上流から下流へ、下流から上流へと往復運動を行います。

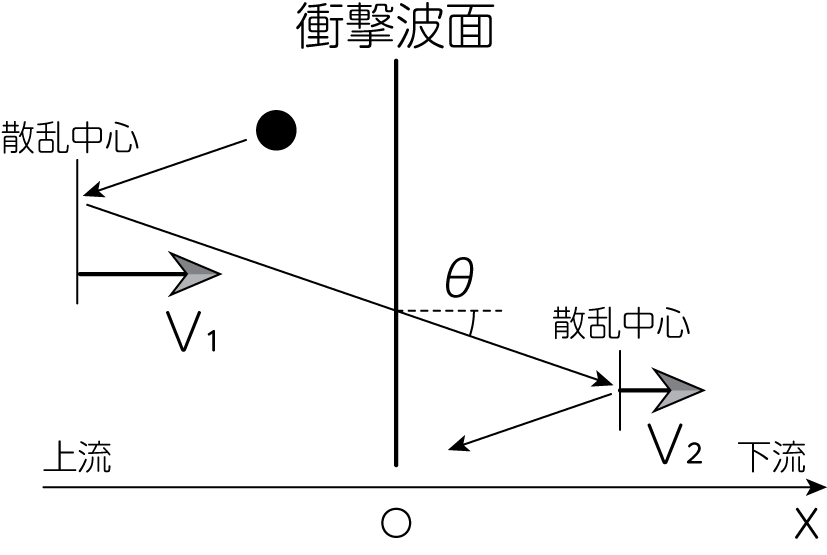
上流の流体と下流の流体は、荷電粒子から見ると互いに近づきあう運動を行っているため、往復するごとに粒子のエネルギーが増加することになります。 1サイクルごとにエネルギーが増加するという意味で、これを1次のフェルミ加速と呼びます。
散乱を起こす波の速度はアルヴェーン速度ですが、これは流体の速度よりはるかに小さく、乱れは基本的に流体と同じ速度で運動していると考えましょう。このとき、流体とともに運動する座標系で見ると、散乱は弾性的に起こるものとします。つまり粒子のエネルギーは変化しませんが、上流と下流とを往復することでエネルギーが増加していくことになります。

粒子加速のメカニズム

先ほどの図から、どの程度の加速が得られるかをみていきましょう。まずは正面衝突と追突を1回ずつだけ行った場合、すなわち衝撃波面を挟んで一往復したときのエネルギー獲得を考えましょう。簡単のため、すでに粒子は超相対論的であるとして\(E \simeq c \vert \mathbf{p} \vert, v \sim c\)の関係が成り立つとします。そして上流の超音速流体の速度を\(V_1\)、下流の亜音速流体の速度を\(V_2\)とします。正面衝突・追突による運動量変化\(\Delta p_{衝突}, \Delta p_{追突}\)はそれぞれ、2次のフェルミ加速のときと同様に

\[\Delta p_{衝突} = \frac{2V_1 E_x}{c^2}, \quad \Delta p_{追突} = -\frac{2V_2 E_x}{c^2} \tag{1}\]

のように与えられます。ここで\(E_x = cp_x = c p \cos \theta\)であり、\(\theta\)は衝撃波面を横切る角度です。すると一往復で粒子が得るエネルギー\(\Delta E\)は

\[\Delta E = c \Delta p = \frac{2 (V_1 - V_2)}{c} E_x \ \Longrightarrow \ \frac{\Delta E}{E} = \frac{2 (V_1 - V_2)}{c} \frac{E_x}{E} = \frac{2 (V_1 - V_2)}{c} \cos \theta \tag{2}\]

のようになります。
実際には様々な角度で衝撃波面を横切る粒子が存在することから、\(\theta\)で平均することを考えましょう。粒子が\(\theta \sim \theta + d\theta\)で衝撃波面を横切る確率\(P(\theta)\)は、幾何学的な因子である\(\sin \theta\)に粒子の\(x\)方向の速度成分である\(\cos \theta\)をかけて

\[P(\theta) d\theta \propto \sin \theta \cos \theta d \theta \tag{3}\]

のように書かれます。確率を全範囲で積分した場合、それは1に規格化されていなければなりません。

\[\int_0^{\pi / 2} \sin \theta \cos \theta d\theta = \frac{1}{2} \int_0^{\pi / 2} \sin 2 \theta d \theta = \frac{1}{2} \tag{4}\]

より、求めたかった確率は

\[P(\theta) d\theta = 2 \sin \theta \cos \theta d\theta \tag{5}\]

となります。これを用いて(2)式を\(\theta\)で平均すると

\[\langle \cos \theta \rangle = 2\int_0^{\pi / 2} \sin \theta \cos^2 \theta d\theta \underbrace{=}_{\mu=\cos\theta} 2 \int_0^1 \mu^2 d\mu = \frac{2}{3} \tag{6}\]

より

\[\left\langle \frac{\Delta E}{E}\right\rangle = \frac{4}{3} \frac{V_1 - V_2}{c} \tag{7}\]

となります。すると一往復後の粒子のエネルギー\(E_1\)は、初期状態のエネルギーを\(E_0\)として

\[E_1 = E_0 + \Delta E = E_0 \left( 1 + \frac{4}{3} \frac{V_1 - V_2}{c}\right) \ \Longrightarrow \ \frac{E_1}{E_0} = 1 + \frac{4}{3} \frac{V_1 - V_2}{c} \tag{8}\]

のようになります。途中、角度の平均操作である\(\langle \cdots \rangle\)は省略しました。以上より、過程を\(\ell\)回繰り返した後の粒子エネルギー\(E_\ell\)は

\[\frac{E_\ell}{E_0} = \left(1+ \frac{4}{3} \frac{V_1 - V_2}{c}\right)^\ell \underbrace{\simeq}_{V_1 - V_2 \ll c} \left( e^{\frac{4}{3} \frac{V_1 - V_2}{c}} \right)^\ell = e^{\frac{4}{3} \frac{V_1 - V_2}{c} \ell} \tag{9}\]

となります。

粒子のエネルギースペクトル

続いて、先ほどのメカニズムで加速された荷電粒子が、衝撃波面近傍の加速領域から逃げていく確率を計算しましょう。上流に行った高エネルギー粒子は、長い時間が経過すると必ず衝撃波面に戻ってきます。そして下流に流された粒子は、先ほどのように追突を起こして再び上流へ戻るものもあれば、そのままさらに下流へ流されて衝撃波面に戻れないものもあるでしょう。そのまま下流に流されてしまう確率を\(P_\mathrm{esc}\)とすると、これは

\[P_\mathrm{esc} = \frac{下流のプラズマに流されて逃げる粒子流束}{上流・下流両方から衝撃波面に流入する粒子流束} \tag{10}\]

のように計算されます。分子は素直に\(N_0 V_2\)のように書けます。分母において、テスト粒子近似から粒子が等方的に存在すると、衝撃波面に流入する粒子の速度の平均は

\[\frac{1}{4\pi} \int_0^{\pi / 2} d\theta \int_0^{2\pi} c \cos \theta \sin \theta d\theta = \frac{c}{4} \int_0^{\pi / 2} \sin 2 \theta d\theta = \frac{c}{4} \tag{11}\]

のように計算されます。以上から

\[P_\mathrm{esc} = \frac{N_0 V_2}{\frac{N_0 c}{4}} = \frac{4V_2}{c} \tag{12}\]

を得ます。すると\(\ell\)回の往復後にまだ粒子が衝撃波面近傍に残って加速されることができる確率は

\[P(\ell) = \left( 1 - P_\mathrm{esc}\right)^\ell = \left( 1 - \frac{4V_2}{c} \right)^\ell \underbrace{\simeq}_{V_2 \ll c} \left( e^{-\frac{4V_2}{c}} \right)^\ell = e^{-\frac{4V_2}{c} \ell} \tag{13}\]

(9)式より

\[\log \left(\frac{E_\ell}{E_0}\right) = \frac{4}{3} \frac{V_1 - V_2}{c} \ell \ \Longrightarrow \ \ell = \log \left( \frac{E_\ell}{E_0} \right)^{\frac{3c}{4(V_1 - V_2)}} \tag{14}\]

一方、(13)式より

\[\log P(\ell) = - \frac{4 V_2}{c} \ell = - \frac{4 V_2}{c} \log \left( \frac{E_\ell}{E_0} \right)^{\frac{3c}{4(V_1 - V_2)}} = \log \left( \frac{E_\ell}{E_0}\right)^{-\frac{3V_2}{V_1 - V_2}} \tag{15}\]

となるため

\[P(\ell) = \left( \frac{E_\ell}{E_0}\right)^{-\frac{3V_2}{V_1 - V_2}} \tag{16}\]

を得ます。ここまで\(\ell\)回の往復する確率\(P(\ell)\)を考えてきましたが、これはエネルギー\(E\)まで粒子が加速される確率\(P(E) = \left( \frac{E}{E_0}\right)^{-\frac{3V_2}{V_1 - V_2}}\)と考えることができます。ここから、粒子のエネルギースペクトルを考えていきましょう。エネルギーが\(E \sim E + dE\)の範囲にある粒子数を\(N(E)dE\)とすると、あるエネルギー\(E\)より大きなエネルギーを持つ粒子の割合は

\[P(E) \propto \frac{\int_E^\infty N(E) dE}{\int_0^\infty N(E) dE} \tag{17}\]

のように考えることができます。この両辺を\(E\)で微分すれば

\[N(E) \propto \frac{dP}{dE} \propto E^{-\frac{3V_2}{V_1- V_2}-1} = E^{-s} \quad \left( s \equiv \frac{V_1 / V_2 + 2}{V_1/ V_2 - 1}\right)\tag{18}\]

のようになり、求めたかった加速粒子のエネルギースペクトル求めることができました。スペクトル指数\(s\)の中に現れる\(V_1 / V_2\)は、衝撃波のランキン・ユゴニオ関係から決定できるマクロな定数です。衝撃波の詳細な物理パラメータに依存することなく、普遍的なものとなりました。非相対論的な断熱(\(\gamma = 5/3\))の衝撃波において、マッハ数が1より非常に大きい場合には、\(V_1 / V_2 =4\)となります。その場合のスペクトル指数は\(s = 2\)となります。これは実際に観測されている、銀河系内起源であるknee以下の宇宙線スペクトルの観測結果\(N(E) \propto E^{-(2.0 \sim 2.2)}\)に非常に近いため、広く受け入れられています。

フェルミ加速で得られる最高エネルギー

衝撃波でのフェルミ加速により、普遍的なスペクトル指数のベキスペクトルが得られることがわかりました。では実際の衝撃波において、どの程度のエネルギーまで加速することができるかを考えてみましょう。衝撃波面を一往復するのにかかる時間を\(\Delta t\)とします。そしてエネルギー\(E\)を持つ粒子が加速されるのにかかる時間\(t_\mathrm{acc}\)を「\(E \rightarrow 2E\)程度までエネルギーが増加するのにかかる時間」というように定義しましょう。すると、この定義から

\[t_\mathrm{acc} = \frac{E}{\Delta E} \Delta t \tag{19}\]

となります。

上流領域の滞在時間

まずは上流側について考えましょう。上流における高エネルギー荷電粒子の粒子流束は以下のように与えられます。

\[\mathbf{J} = -\kappa_1 \nabla N + N \mathbf{V}_1 \ \Longrightarrow \ J_x = - \kappa_1 \frac{dN}{dx} + N V_1 \tag{20}\]

ここで\(\kappa_1\)は上流領域での拡散係数、\(\mathbf{V}_1\)は上流での流体の速度です。これまでの問題設定から、\(x\)方向のみを考えることにします。また\(x = 0\)を衝撃波面の位置としましょう。加速された粒子が一定の割合で逃げ出していくことにより平衡状態が維持されているとすると、\(J_x=0\)より

\[\frac{dN}{dx} = \frac{V_1}{\kappa_1} N \ \Longrightarrow \ N(x) = N_0 e^{\frac{V_1}{\kappa_1} x} \quad (x<0) \tag{21}\]

(21)式を\(x\)で積分することで、単位面積あたりの総粒子数(柱密度)\(n\)は

\[n = \int_{-\infty}^0 N_0 e^{\frac{V_1}{\kappa_1} x} dx = \frac{N_0 \kappa_1}{V_1} \tag{22}\]

のように計算されます。途中、\(N(-\infty) = 0\)としました。 (11)式より、衝撃波面に流入する平均粒子流束は\(N_0 c/4\)であることから、粒子が上流に滞在する平均時間\(\Delta t_{上流}\)は

\[\Delta t_{上流} = \frac{\frac{N_0 \kappa_1}{V_1}}{\frac{N_0 c}{4}} = \frac{4 \kappa_1}{cV_1} \tag{23}\]

のようになります

下流領域の滞在時間

粒子が下流に滞在する平均時間を考えるために、次のようなモデル化を行いましょう。 \(x = 0\)に吸収境界(\(N(0)=0\))が存在し、\(x = x_0 (>0)\)の下流に粒子の注入ソースがあるような系を考えます。下流領域の拡散係数を\(\kappa_2\)とすると

\[V_2 \frac{\partial N}{\partial x} = \kappa_2 \frac{\partial^2 N}{\partial x^2} + Q\delta (x - x_0) \tag{24}\]

のように方程式を立てることができます。この解は

\[N = \left\{ \begin{array}{ll} \frac{Q}{V_2} (e^{\frac{V_2 x}{\kappa_2}}-1) e^{-\frac{V_2 x_0}{\kappa_2}} & (0 \leq x \leq x_0) \\ \frac{Q}{V_2} (1-e^{-\frac{V_2 x}{\kappa_2}}) & (x_0 \leq x) \end{array} \right. \tag{25}\]

となります。 \(x = 0\)における粒子流束を計算しましょう。すると

\[\left. \frac{\partial N}{\partial x} \right|_{x=0} = \left. \frac{Q}{\kappa_2} e^{\frac{V_2 (x-x_0)}{\kappa_2}} \right|_{x=0} = \frac{Q}{\kappa_2} e^{-\frac{V_2 x_0}{\kappa}} \ \Longrightarrow \ \kappa_2 \frac{\partial N}{\partial x} = Q e^{-\frac{V_2 x_0}{\kappa_2}} \tag{26}\]

となります。これは\(x=x_0\)で注入された\(Q\)個の粒子のうち、\(P_\mathrm{return} = e^{-\frac{V_2 x_0}{\kappa_2}}\)の割合だけ\(x=0\)に戻ることができることを意味します。下流の流体速度である\(V_2\)が大きいと、粒子が下流に流されるために\(x=0\)に戻る割合が少なくなり、また\(\kappa_2\)が大きいと拡散により\(x=0\)に戻りやすくなるという直感に一致します。これを\(x_0\)の取りうる全範囲で積分すれば、それが下流領域全体から衝撃波面に戻る粒子の割合を求めたことになります。

\[N_0 \int_0^\infty e^{-\frac{V_2 x_0}{\kappa_2}} dx_0 = \frac{N_0 \kappa_2}{V_2} \tag{27}\]

これを(11)式からの衝撃波面に流入する平均粒子流束\(N_0 c/4\)で割れば、粒子が下流に滞在する平均時間\(\Delta t_{下流}\)になります。

\[\Delta t_{下流} = \frac{4 \kappa_2}{cV_2} \tag{28}\]

以上より一往復にかかる時間\(\Delta t = \Delta t_{上流} + \Delta t_{下流}\)から、加速にかかる時間は

\[t_\mathrm{acc} = \frac{3}{4} \frac{c}{V_1 - V_2} \left( \frac{4 \kappa_1}{cV_1} + \frac{4 \kappa_2}{cV_2}\right) = \frac{3}{V_1 - V_2} \left( \frac{\kappa_1}{V_1} + \frac{\kappa_2}{V_2}\right) \tag{29}\]

となります。ここで注意すべきことは、加速時間が流れの速度の2乗に反比例していることです。つまり1次のフェルミ加速という名前ですが、加速時間については2次となっていることがわかります。ただし星間雲の乱流運動を利用した元々のフェルミ加速と異なり、衝撃波の速度は乱流運動速度よりも何桁も大きいため、加速時間が十分に短くなり得ます。

フェルミ加速の検証

フェルミ加速で得られる最大エネルギーを、大雑把に求めてみましょう。簡単のため(29)式において、\(\kappa_1 = \kappa_2 = \kappa\)、そして\(V_1 = 4V_2 = V_s\)のようにすると

\[t_\mathrm{acc} = \frac{3 \kappa}{\frac{3}{4} V_s} \left( \frac{1}{V_s} + \frac{4}{V_s}\right) = \frac{20\kappa}{V_s^2} \tag{30}\]

と求まります。これを計算するには、拡散係数\(\kappa\)の値を定める必要があります。ここでの高エネルギーの荷電粒子は、アルヴェーン波などの磁場の乱れによるものと考えられるため、次のような表現を用いることにしましょう。

\[\kappa = \frac{1}{3} v r_L \left( \frac{B}{\delta B} \right)^2 \equiv \frac{1}{3} v r_L \xi \tag{31}\]

ここで\(r_L = \frac{cp}{ZeB}\)は、電荷\(Ze\)を持つ粒子のジャイロ半径です。また\(\xi\)は磁場の乱れの程度を表すもので、乱れの大きさがもとの磁場と同程度にある大きな乱れの極限(\(\xi =1\))をボーム極限と呼びます。超新星残骸などの活動天体では直接的な観測は困難です。しかし、太陽風中の衝撃波中の磁場観測による類推から、\(\xi \sim 10\)程度とされています。よって以下では\(1 \leq \xi \leq 10\)として議論を進めましょう。 (30)式の整理を進めましょう。粒子の速度は超相対論的であるとして、\(v \sim c, E = cp\)が成り立つとすると

\[t_\mathrm{acc} = \frac{20}{3}\frac{c^2 p}{Ze V_s^2 B} \xi = \frac{20}{3}\frac{c E}{Ze V_s^2 B} \xi \tag{32}\]

のようになります。先程まで述べたフェルミ加速機構は、粒子のエネルギーに依存しませんでした。しかし、この場合には加速時間\(t_\mathrm{acc}\)はエネルギーに依存することに注意が必要です。 (32)式より、単位時間あたりの平均のエネルギー増加率が

\[\frac{E}{t_\mathrm{acc}} = \frac{3}{20} \frac{Z e V_s^2 B}{c \xi} \tag{33}\]

のように求まります。ここから、経過時間\(t_\mathrm{ev} \sim R / V_s\)後のエネルギーが

\[\begin{align} E_\mathrm{max} &\simeq \frac{3}{20} \frac{Z e V_s B R}{c \xi} = \frac{3}{20} \frac{Z}{\xi} \frac{e V_s B R}{c} = \frac{3}{20} \frac{Z}{\xi} \left(\frac{V_s}{10^4 \mathrm{km/s}} \right) \left(\frac{B}{10 \mu \mathrm{G}} \right) \left( \frac{R}{10 \mathrm{pc}}\right) \frac{e }{c} \notag \\ &\simeq 4.5 \times 10^{14} \frac{Z}{\xi} \left(\frac{V_s}{10^4 \mathrm{km/s}} \right) \left(\frac{B}{10 \mu \mathrm{G}} \right) \left( \frac{R}{10 \mathrm{pc}}\right) \ [\mathrm{eV}] \tag{34} \end{align}\]

とわかります。ここで\(R\)は球形の超新星残骸の半径であり、超新星爆発の衝撃波が\(V_s\)で宇宙空間に伝搬していると考えました。超新星残骸の典型的なパラメータをとると、陽子が10-100TeV程度まで加速されることがわかります。さらに鉄原子(\(Z = 26\))であれば、PeV (=\(10^{15}\)eV)領域まで到達できると予想されます。

ペバトロンの観測

最後に、実際に観測されている高エネルギー天体について触れておきましょう。最近の観測で、はくちょう座方向にある星形成領域 Cygnus X から、数PeVの超高エネルギーγ線が観測されました。この超高エネルギーγ線は少なくとも10PeV以上の加速陽子からの放射であるとされ、この領域がPeV粒子を生み出すペバトロン(PeVatron: エネルギーの単位ペブに粒子加速器などのトロンをつけた造語)であると結論づけました。この観測はthe Large High Altitude Air Shower Observatory (LHAASO)を用いて行われ中心部はCygnus OB2と呼ばれるOB association (O型星やB型星などの大質量星が群をなしているような領域)と、Cygnus X-3と呼ばれるマイクロクエーサー(コンパクト星を含む連星系からなる)を含んでいます。この部分から2つのPeV光子が観測され、またその周囲からも数百TeVのγ線が観測されています。この観測結果からコア部分が最高エネルギーまで粒子を加速し、加速された宇宙線が周囲に拡がっていくという、一般的なバブルの形態が再現されているとしました。

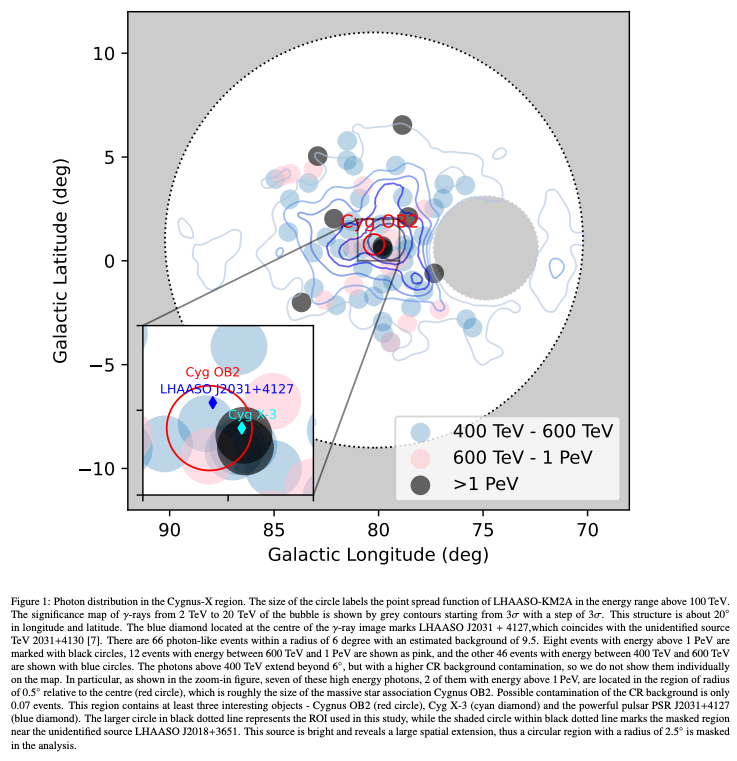
そのほかにもthe High-Altitude Water Cherenkov gamma-ray observatory (HAWC)による観測結果から、天の川銀河中心方向にペバトロンが存在するという論文も発表されています。このようなペバトロンでは、これまで考えてきたようなフェルミ加速による宇宙線生成が起こっていると考えられています。

参考文献

[1] Drury, 1983, “An introduction to the theory of diffusive shock acceleration of energetic particles in tenuous plasmas”
[2] LHASSO Collaboration, 2024, “An Ultrahigh-energy γ-ray Bubble Powered by a Super PeVatron”
[3] LHASSO
[4] Albert et al., 2024, “Observation of the Galactic Center PeVatron beyond 100 TeV with HAWC”
[5] HAWC
[6] 高原文朗, “天体高エネルギー現象”
[7] 星野真弘, “相対論的粒子加速と宇宙線の起源”
[8] 鶴剛, “京都大学大学院物理専攻大学院授業「高エネルギー天文学」講義ノート”