ラザフォード散乱
陽子による電子の散乱の問題を考えましょう。ただし、陽子(938MeV)は電子(511keV)よりも1840倍も質量が大きいので、以下では陽子は重心に静止していると考えます。
角運動量保存
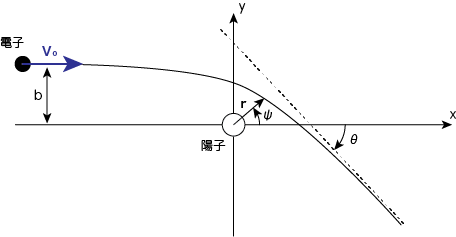
陽子の位置を原点とします。電子はクーロン力(中心力)のみを受けて運動するため、角運動量保存から\(xy\)平面内に限られます。
図のように原点から距離\(r\)と角度\(\psi\)を取る座標基底の単位ベクトルは
のように書かれます。これを用いて電子の位置・運動量・角運動量を記述しましょう。すると
\[\mathbf{r} =r\mathbf{e}_r , \quad \mathbf{p} = m_e \dot{\mathbf{r}} = m_e( \dot{r} \mathbf{e}_r + r \dot{\psi} \mathbf{e}_\psi) , \quad \mathbf{L} = \mathbf{r} \times \mathbf{p} = m_e r^{2} \dot{\psi} \mathbf{e}_z \tag{1}\]初期状態として、電子は無限遠方の\(x\)負方向から初速度\(V_0\)、衝突パラメータ\(b\)で撃ち込まれたと考えます。すると無限遠方にいあるときの角運動量は上図から
\[\mathbf{L} = -m_e V_0 b \mathbf{e}_z \tag{2}\]と書けます。角運動量が保存するので、(1), (2)式より
\[\dot{\psi} = -\frac{b V_0}{r^2} \tag{3}\]となります。
散乱角度の導出
電子の運動方程式から
\[m_{e} \left( \begin{array}{c} \frac{d v_{x}}{dt} \\ \frac{d v_{y}}{dt} \\ \frac{d v_{z}}{dt} \\ \end{array} \right) = - \frac{e^{2}}{r^{2}} \mathbf{e}_r = - \frac{e^{2}}{r^{2}} \left( \begin{array}{c} \cos \psi \\ \sin \psi \\ 0 \\ \end{array} \right)\]ここで(3)式より
\[\frac{d}{dt} = \frac{d \psi}{dt} \frac{d}{d \psi} = - \frac{b V_{0}}{r^{2}} \frac{d}{d \psi}\]と変形できるため
\[\left( \begin{array}{c} \frac{d v_{x}}{d \psi} \\ \frac{d v_{y}}{d \psi} \\ \frac{d v_{z}}{d \psi} \\ \end{array} \right) = \frac{e^{2}}{m_{e}bV_{0}} \mathbf{e}_r\]のようになります。この式の両辺を\(\psi\)で積分すれば、電子の速度\(\mathbf{v}\)が求まります。積分範囲は無限遠方から撃ち込まれたとき\(\psi=\pi\)、散乱後は\(\psi = -\theta\)の方向に飛び去るので
\[\int_\pi^{-\theta} (\mathrm{R.H.S}) \ d\psi = \frac{e^{2}}{m_{e}bV_{0}} \int_{\pi}^{- \theta} \mathbf{e}_r d\psi = - \frac{e^{2}}{m_{e}bV_0} \left. \mathbf{e}_\psi \right|_{\pi}^{- \theta} = - \frac{e^{2}}{m_{e} bV_0} \left( \begin{array}{c} \sin \theta \\ \cos \theta + 1\\ 0 \\ \end{array} \right)\]初期状態の電子の速度ベクトルと散乱どの電子の速度ベクトルをそれぞれ\(\mathbf{v}(t=0), \mathbf{v}(t=\infty)\)とすると、エネルギー保存より電子の速度の大きさは散乱前後で変化しないから
\[\int_\pi^{-\theta} (\mathrm{L.H.S}) \ d\psi = \int_{\mathbf{v}(0)}^{\mathbf{v}(\infty)} d {\bf v} = V_{0} \left( \begin{array}{c} \cos \theta \\ \sin \theta \\ 0 \\ \end{array} \right) - V_{0} \left( \begin{array}{c} 1 \\ 0 \\ 0 \\ \end{array} \right) = V_{0} \left( \begin{array}{c} \cos \theta - 1\\ - \sin \theta \\ 0 \\ \end{array} \right)\]左辺と右辺の計算結果から、その\(x\)成分を比較することにより
\[\frac{m_{e} b {V_{0}^{2}}}{e^{2}} = \frac{\sin \theta}{1 - \cos \theta} = \frac{\cos \frac{\theta}{2}}{\sin \frac{\theta}{2}} = \cot \frac{\theta}{2} \tag{4}\]となります。
大角度散乱
\(\theta \geq \pi/2\)となるような、大きな角度の散乱が起こる条件を求めてみましょう。(4)より
\[\frac{m_e b V_0^2}{e^2} \leq 1 \ \Longrightarrow \ m_e V_0^2 \leq \frac{e^2}{b} \tag{5}\](5)式から、\(\pi/2 \leq \theta \leq \pi\)のような大角度散乱は、電子が陽子に一番接近したときのクーロンポテンシャルよりも、入射電子の運動エネルギーが小さいときに起こると見積もることができます。
(4)式の\(\cos \frac{\theta}{2}\)の概形からも分かる通り、\(b \rightarrow 0\)では\(\theta \rightarrow \pi\)、\(b \rightarrow \infty\)では\(\theta \rightarrow 0\)となります。この散乱角度は\(b\)が大きくなるほど(電子と陽子のすれ違いの距離が大きくなるほど)散乱角度が小さくなる、という直感的なものと一致します。
微分散乱断面積
ここまでは1個の電子を入射させることを考えてきましたが、今度は無限遠方から個数密度\(n\)、初速度\(V_0\)で電子ビームが入射してくるような状況を考えましょう。ただし電子同士の相互作用は無視します。
無限遠方での電子の入射個数の流束(flux)、すなわち単位時間あたりに単位面積を通過する電子の個数\(I\)は
です。次の図のように、半径\(b\), 幅\(db\)の細いリングを通過した電子が、角度\(\theta\)から\(\theta + d\theta\)の方向に散乱されたと考えます。
![微分散乱断面積の考え方。幅dbの間に撃ち込まれた電子が[θ, θ+dθ]の間に飛び去ると考える](/assets/images/ism/rutherford_02.png)
(4)式より
\[db = \frac{e^2}{m_e {V_0}^2} \frac{- \frac{1}{2} \sin^2 \frac{\theta}{2} - \frac{1}{2} \cos^2 \frac{\theta}{2}}{\sin^2 \frac{\theta}{2}} d\theta = - \frac{e^2}{2 m_e {V_0}^2} \frac{1}{\sin^2 \frac{\theta}{2}} d\theta\]単位時間に\(\theta, \phi\)方向に散乱された電子の数を\(N\)とすると、その定義より
\[\begin{aligned} 2 \pi N \sin \theta d \theta &= I \cdot 2 \pi b | db | = n V_{0} \pi {\left(\frac{e^{2}}{m_{e} {V_{0}}^{2}}\right)}^{2} \frac{\cot \frac{\theta}{2}}{\sin^{2} \frac{\theta}{2}} d \theta = n V_0 \pi \left( \frac{e^2}{m_e {V_0}^2}\right)^2 \frac{2 \sin \frac{\theta}{2} \cos \frac{\theta}{2}}{2 \sin^4 \frac{\theta}{2}} d\theta \\ &= n V_0 \pi \left( \frac{e^2}{m_e {V_0}^2}\right)^2 \frac{\sin \theta}{2 \sin^4 \frac{\theta}{2}} d\theta \end{aligned}\]となります。\(x\)軸に対して軸対称な系なので、\(\phi\)方向はすでに積分して\(2\pi\)としています。また\(db\)は\(b\)が増加すると散乱角度\(\theta\)が減少することから、辻褄を合わせるために絶対値としています。以上より
\[N = \frac{n V_{0}}{4} {\left( \frac{e^{2}}{m_{e} {V_{0}}^{2}} \right)}^{2} \frac{1}{\sin^{4} \frac{\theta}{2}} \tag{6}\]Flux \(I\)で入射してきた電子群が面積\(d \sigma_R\)にぶつかり、角度\(\theta, \phi\)方向の微小立体角\(d\Omega\)に散乱されたと考えましょう。微分散乱断面積を以下のように定義します。
\[I \frac{d \sigma_\mathrm{R} (\theta, \phi)}{d \Omega} = N \tag{7}\]\(\frac{d \sigma_\mathrm{R} (\theta, \phi)}{d \Omega}\)を微分散乱断面積と呼びます。(6), (7)式より
\[\frac{d \sigma_\mathrm{R}}{d \Omega} = {\left( \frac{e^{2}}{2 m_e {V_{0}}^{2}} \right)}^{2} \frac{1}{\sin^{4} \frac{\theta}{2}} \tag{8}\]これより\(\theta=0\)のとき微分散乱断面積は無限大に発散し、\(\theta=\pi\)のとき最小となることがわかります。これは\(\theta=0\)に散乱される割合が最も高く、\(\theta=\pi\)に散乱される割合が最も低いという意味です。\(\theta=\pi\)のときは、入射電子が初速度とは反対方向に散乱される場合です。これは電子と陽子が正面衝突するときに限られるため、この割合が一番低くなることは直感と一致します。
散乱断面積
微分散乱断面積\(\frac{d\sigma_\mathrm{R}}{d\Omega}\)は面積の次元を持ちます。すなわち、これはある\(\theta, \phi\)方向に散乱される場合の「まと」の大きさを表しています。それを全立体角で積分したものは(どの方向に散乱されるかはともかくとして)散乱を受けるときのまとの大きさになることがわかります。ラザフォード散乱の場合に求めてみると
\[\sigma_\mathrm{R} = \left( \frac{e^2}{2 m_e {V_0}^2}\right)^2 2 \pi \int_{0}^{\pi} \frac{\sin \theta}{\sin^4 \frac{\theta}{2}} d \theta \propto \int_{0}^{\pi} \frac{\cos \frac{\theta}{2}}{\sin^3 \frac{\theta}{2}}d\theta \propto \int_{0}^{1} \frac{d x}{x^3}\]となって無限大に発散します。これはクーロン力が\(r^{-2}\)に比例する長距離力であるため、どんなに衝突パラメータ\(b\)が大きくても「散乱された電子」としてカウントされてしまうためです。全立体角で積分すると、ほんのわずかしか散乱を受けていない電子も勘定してしまうため、このような結果となります。よってここでは散乱角度が\(\pi/2 \leq \theta \leq \pi\)の、大角度散乱された粒子のみを考えましょう。電子の大角度散乱のラザフォード散乱断面積は
\[\sigma_\mathrm{R} = \frac{1}{4} {\left( \frac{e^{2}}{m_{e} {V_{0}}^{2}} \right)}^{2} 2\pi \int_{\pi / 2}^{\pi} \sin \theta \frac{d \theta}{\sin^4 \frac{\theta}{2}} = \pi {\left( \frac{e^{2}}{m_{e} {V_{0}}^{2}} \right)}^{2} \tag{9}\]となります。\((\cdots)^2\)の中身は、最も散乱頻度の高い\(\theta=\pi/2\)となるときの衝突パラメータに等しくなっています。(9)式から、電子にとって陽子はこれを半径とした円盤のまとであることがわかります。
まとめると、全散乱断面積とは衝突時のまとの面積の大きさを表すものです。微分散乱断面積\(\frac{d\sigma}{d\Omega}\)は、入射fluxが\(I=1\)のとき、角度\(\theta, \phi\)の方向を中心とした微小立体角\(d\Omega\)に散乱されて出ていく電子の数を与えます。ランダムに粒子を入射させたときに、ある方向に散乱されて出てくる確率に比例した量と考えることもできます。
参考文献
- [1] 須藤靖, 解析力学・量子論