潮汐力と潮汐破壊現象

ここでは中心天体の周囲を回る惑星やその他の天体が、中心天体から受ける潮汐力(tidal force)について勉強したものをメモします。また、主に超大質量ブラックホールによる強烈な潮汐力により、その周囲を回る恒星が引き裂かれる潮汐破壊現象(Tidal Disruption Events: TDEs)についても記述しています。

潮汐ポテンシャル

潮汐力を考えるにあたり、ここでは2つの恒星からなる連星系について考えましょう。中心に位置する、質量\(M_2\)の恒星を恒星2とします。この星からの重力により引き起こされる、質量\(M_1\)の恒星1の変形を計算します。座標原点を恒星1の中心とし、さらに恒星1の内部のある点の位置ベクトルを\(\mathbf{r}\)とすると、その点における重力ポテンシャルは

\[\Phi (\mathbf{r}) = \Phi_1 (\mathbf{r}) + \Phi_2 (\mathbf{r})\tag{1}\]

のように、恒星1の自己重力ポテンシャルと恒星2の重力ポテンシャルの総和として書かれます。

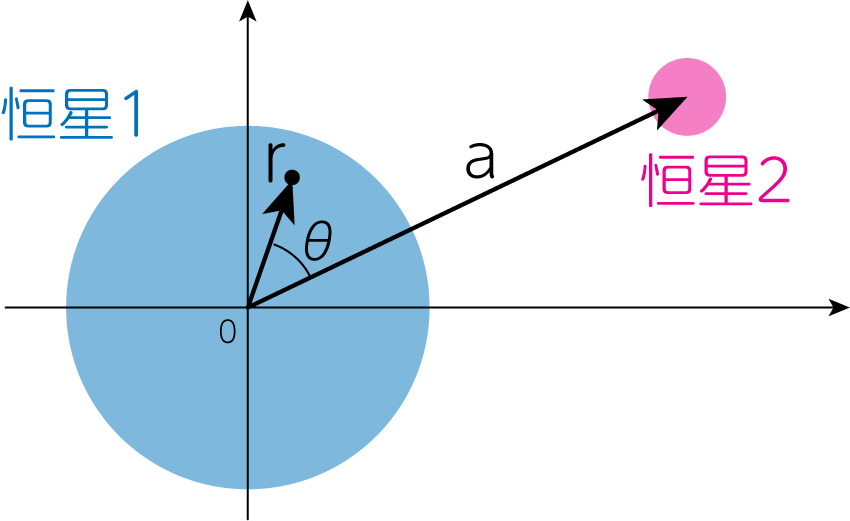
\(\Phi_2\)は恒星2の外部における重力ポテンシャルなので

\[\Phi_2 = - \frac{GM_2}{\vert \mathbf{r}-\mathbf{a} \vert} \tag{2}\]

のように記述されます。ここで\(\mathbf{a}\)は恒星2の位置ベクトルを表します。 (2)式において、\(r < a\)としてルジャンドル展開すると

\[\Phi_2 = - \frac{GM_2}{a} \left\{ 1 + \frac{r}{a} P_1(\cos \theta) + \frac{r^2}{a^2} P_2 (\cos \theta) + \cdots \right\} \tag{3}\]

となります。ここで\(P_n(\cos \theta)\)はルジャンドル多項式、そして\(\theta\)は\(\mathbf{r}\)と\(\mathbf{a}\)の成す角度を表します。求めたいのは恒星1がどれだけ変形しているか、です。よって変形を生じさせる力を求めるために、(3)式の勾配を計算していきましょう。勾配計算は極座標系で行います。第一項は定数なので無視できます。第二項からは

\[\mathbf{F}_2 = -\nabla \left\{-\frac{GM_2}{a} \frac{r}{a} P_1(\cos \theta)\right\} = \frac{GM_2}{a^2} P_1(\cos \theta) \frac{\partial r}{\partial r} \mathbf{e}_r + \frac{GM_2}{a^2} r \frac{1}{r} \frac{\partial}{\partial \theta} P_1 (\cos \theta) \tag{4}\]

のように計算がされます。ルジャンドル多項式の具体的な形から\(P_1 (\cos \theta) = \cos \theta\)を入れて、さらに計算を進めましょう。

\[\mathbf{F}_2 = \frac{GM_2}{a^2} (\cos \theta \mathbf{e}_r - \sin \theta \mathbf{e}_\theta) \tag{5}\]

\(\mathbf{e}_r \cdot \mathbf{a} = a \cos \theta, \mathbf{e}_\theta \cdot \mathbf{a} = -a \sin \theta\)より、最終的に

\[\mathbf{F}_2 = \frac{GM_2}{a^2} \frac{\mathbf{a}}{a} \tag{6}\]

を得ます。ここまでは恒星1の中心を座標原点としてきましたが、この座標系は連星系の質量中心の周りを公転運動しているため、見かけの力が現れます。これは遠心力として考えることができます。遠心力は

\[\mathbf{F}_\mathrm{centrifugal} = \frac{M_2 a}{M_1 + M_2} \Omega^2 \left( - \frac{\mathbf{a}}{a} \right) \tag{7}\]

のように書かれます。ここで\(\Omega\)は連星の軌道周期です。このとき、ケプラーの第三法則より

\[\Omega^2 = \left( \frac{2\pi}{P} \right)^2 = \frac{G(M_1 + M_2)}{a^3} \tag{8}\]

から

\[\mathbf{F}_\mathrm{centrifugal} = - \frac{GM_2}{a^2} \frac{\mathbf{a}}{a} \tag{9}\]

となります。これは(7)式にマイナス符号をつけたものと全く同じ形です。よってこれらは打ち消し合い、恒星1の変形には寄与しません。したがって、恒星1に変形をもたらす最初の項は

\[\Phi_\mathrm{tidal} = - \frac{GM_2}{a} \frac{r^2}{a^2} P_2 (\cos \theta) \tag{10}\]

とわかります。これを潮汐ポテンシャルと呼びます。

潮汐力

ここから、潮汐力を計算しましょう。 \(P_2 (\cos \theta) = \frac{1}{2} (3 \cos^2 \theta - 1)\)より

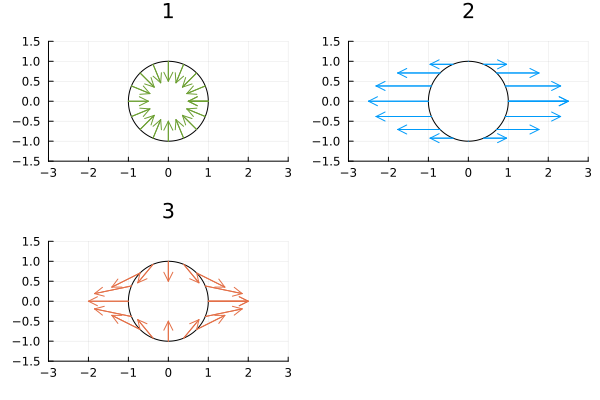
\[\begin{align} \mathbf{F}_\mathrm{tidal} &= - \nabla \left\{ -\frac{GM_2}{a} \frac{r^2}{a^2} \frac{1}{2} (3 \cos^2 \theta - 1)\right\} \notag \\ &= \frac{GM_2}{a^3} \frac{\partial r^2}{\partial r} \frac{1}{2} (3 \cos^2 \theta - 1) \mathbf{e}_r + \frac{GM_2 r^2}{2a^3} \frac{1}{r} \frac{\partial}{\partial \theta} (3\cos^2 \theta - 1) \mathbf{e}_\theta \notag \\ &= \frac{GM_2}{a^3} r (3 \cos^2 \theta - 1) \mathbf{e}_r + \frac{GM_2 r}{2a^3} (- 6 \cos \theta \sin \theta) \notag \\ &= - \frac{GM_2}{a^2} \frac{r}{a} \mathbf{e}_r + \frac{3GM_2}{a^2} \frac{r}{a} \cos \theta (\cos \theta \mathbf{e}_r - \sin \theta \mathbf{e}_\theta) = - \frac{GM_2}{a^2} \frac{r}{a} \mathbf{e}_r + \frac{3GM_2}{a^2} \frac{r}{a} \cos \theta \frac{\mathbf{a}}{a} \tag{11} \end{align}\]

これが潮汐力です。第一項は恒星1の中心に向かう力です。すなわち、恒星1を潰そうとするように働きます。第二項は常に\(\mathbf{a}/a\)の方向を向いていますが、最大となるのは\(\theta = 0, \pi\)の位置です。その向きは恒星1を引き伸ばすように働きます。下図は(1). 第一項、(2). 第二項、(3). 二つを足し合わせたもの、を可視化したものです。この図では、恒星2は\(x\)軸上にいるとしています。

潮汐半径 (tilda radius)

潮汐半径とは、潮汐力で天体がバラバラに分解されない距離を表します。この距離より外側を通過するならば、天体は(潮汐力で多少は歪むかもしれませんが)無事に通り過ぎることができます。しかしこの距離より内側を通過する場合、天体は潮汐力により大きく変形し、最終的にバラバラにされてしまいます。先程の潮汐力(11)式から、この距離を大雑把に見積もってみましょう。 \(r = R_1\)のように、恒星1の表面での力の大きさの比較から考えます。すると潮汐力の大きさは、大雑把に

\[F_\mathrm{tidal} \simeq \frac{GM_2 R_1}{a^3} \tag{12}\]

です。この力が、恒星1の自己重力による束縛より大きいときに恒星1がバラバラにされてしまう、と考えましょう。

\[\frac{GM_2 R_1}{a^3} \geq \frac{GM_1}{R_1^2} \ \Longrightarrow \ a \leq R_1 \left( \frac{M_2}{M_1}\right)^{1/3} \tag{13}\]

この\(a_t \equiv R_1 (M_2/ M_1)^{1/3}\)を潮汐半径と呼びます。これより内側を通過する恒星は、潮汐力によりバラバラにされてしまい、一部は中心天体に降り注ぎます。ここまでは中心天体をコンパクト天体(ブラックホールなど)などとして考えてきました。しかし、この現象は銀河スケールでも起こります。天の川銀河周辺には大小様々な衛星銀河が存在し、それらが潮汐力で変形した様子や、恒星が剥ぎ取りを受けている様子も確認されています。いて座矮小楕円銀河(Sagittarius Dwarf Elliptical Galaxy)が恒星の剥ぎ取りを受けたことで形成されたいて座ストリーム(Sagittarius stream)が有名です。

潮汐破壊現象 (Tidal Disruption Events: TDEs)

先述の通り、この潮汐半径よりも恒星2に近づくと、潮汐力により恒星1はバラバラに分解されます。 \(M_2\)が超大質量ブラックホール(SMBH)のように大質量であるならば、(13)式から潮汐半径が大きくなります。 AGN中心にあるSMBH近傍に恒星が近づくと、恒星が潮汐力で破壊されます。これを潮汐破壊現象(Tidal Disruption Events: TDEs)と呼びます。 TDEの存在は、理論的には1970年代には予言されていました。それが観測されるようになったのは、1990年代に入ってからです。発見された当初は数例しか見つかっていなかったため、どのような現象かはあまり理解されていませんでした。最近の観測技術の発展にしたがって多数のTDEが発見されるようになり、その詳細な姿が明らかにされつつあります。もしSMBHの事象の地平線の外側で太陽型の恒星がTDEを起こすと、遠くにいる我々からはAGNが明るいフレアを起こしたように見えます。また、恒星がバラバラにされて散らばったガスがSMBHに降り注ぐことで、そのSMBH周辺は降着円盤やジェットのリアルタイム生成現場となります。このような理由からTDEは最近注目を集めている、ホットな天体現象です。

潮汐破壊を受けない？謎のガス雲 G2

2011年、天の川銀河中心のSMBH付近を通過するガス雲 G2が発見されました。 2013年ごろにはG2は楕円軌道の近点を通過、すなわちSMBHに最も接近するだろうと考えられており、このときに潮汐力によって破壊されるだろうと思われました。これを見越して様々な理論・数値計算による研究がなされました。それらの研究では、G2は潮汐力により破壊され、一部はSMBHに落下するなどとされていたのです。これにより天の川銀河中心のSMBHが明るく輝くのではないか、と考えられました。また潮汐力によりG2が縦方向の圧縮を受け、G2自身も明るく輝くだろうと予想されていました。

しかし2014年、のちにノーベル物理学賞を受賞するGhez氏の研究グループが、衝撃的な論文を発表します。それは「ガス雲G2は生き延び、その後も何事もなかったかのように楕円軌道を描いて飛び去っていった」というものでした。 G2はただのガス雲ではなく、球状星団のようなよりコンパクトな天体だったおかげで生き残れたのではないか、などの憶測がなされました。しかし、未だその全容は謎に包まれたままです。事実は小説よりも奇なり、とはまさにこのことを言うのでしょう。

補遺: 描画に使用したJuliaコード

以下に、描画に使用したJuliaコードを掲載します。ただし、ここでは見やすさのために\(r = 1.0, k \equiv \frac{GM_2}{a^3} = 0.5\)のようにしています。

using Plots

# set the number of the vectors
len = 16 + 1
# set angles of the starting point of the vectors 
theta1 = range(0.0, 2pi, length=len)
# set the radius
r1 = 1.0
# compute the coordinates of the starting point
x1 = r1 * cos.(theta1)
y1 = r1 * sin.(theta1)
# set the coefficient
k = 0.5
# compute the first term of tidal force
first_x = - k * x1
first_y = - k * y1
# compute the second term of tidal force
second_x = 3 * k * cos.(theta1)
second_y = zeros(Float64, len)
# compute first + second
total_x = first_x + second_x
total_y = first_y + second_y
# set angles for drawing circle
theta2 = range(0.0, 2pi, length=256)
x2 = cos.(theta2)
y2 = sin.(theta2)
# make plot 
plt1 = plot(x2, y2, c=:black, legend=false)
plt1 = quiver!(x1, y1, quiver=(first_x, first_y), aspect_ratio=:equal, xlims=(-3, 3), ylims=(-1.5, 1.5), c=0, title='1')
plt2 = plot(x2, y2, c=:black, legend=false)
plt2 = quiver!(x1, y1, quiver=(second_x, second_y), aspect_ratio=:equal, xlims=(-3, 3), ylims=(-1.5, 1.5), c=1, title='2')
plt3 = plot(x2, y2, c=:black, legend=false)
plt3 = quiver!(x1, y1, quiver=(total_x, total_y), aspect_ratio=:equal, xlims=(-3, 3), ylims=(-1.5, 1.5), c=2, title='3')
plot(plt1, plt2, plt3)
# save figure
savefig("tidal_01.png")

参考文献

[1] Ramos et al., 2021, “The Sagittarius stream in Gaia eDR3 and the origin of the bifurcations”
[2] Saitoh et al., 2014, “Flaring up of the compact cloud G2 during the close encounter with Sgr A*”
[3] Witzel et al., 2014, “Detection of Galactic Center Source G2 at 3.8µm during Periapse Passage”
[4] 連星系に関する問題 –Roche問題、潮汐力–
[5] 川名好史朗, “ブラックホールによる白色矮星の潮汐破壊現象”