ビアマンバッテリー効果による磁場生成

ここでは、初期に磁場が存在しない状態から磁場を発生させる物理機構の一つとして知られるビアマンバッテリー(Biermann battery)についてまとめています。

ビアマンバッテリー (Biermann battery)

完全電離しているプラズマガスにおける電子の運動方程式を考えましょう。電子とイオンの衝突は無視できるとすると

\[m_e n_e \frac{D \mathbf{v}_e}{Dt} = - \nabla P_e - e n_e \left( \mathbf{E} + \mathbf{v} \times \frac{\mathbf{B}}{c} \right) \tag{1}\]

のようになります。ここで\(\mathbf{v}, n_e, P_e\)はそれぞれ磁気流体の速度、電子数密度、電子による分圧です。電子に働く力は釣り合っているとすると、左辺の加速度はゼロより

\[\mathbf{E} = - \mathbf{v} \times \frac{\mathbf{B}}{c} - \frac{\nabla P_e}{en_e} \tag{2}\]

を得ます。これをファラデーの法則に代入すると

\[\frac{\partial \mathbf{B}}{\partial t} = - c \nabla \times \mathbf{E} = \nabla \times (\mathbf{v} \times \mathbf{B}) + \frac{c}{e} \nabla \times \left( \frac{\nabla P_e}{n_e}\right) \tag{3}\]

となります。右辺第二項を整理しましょう。

\[\nabla \times \left( \frac{\nabla P_e}{n_e}\right) = \epsilon_{ijk} \partial_j \left( \frac{\partial_k P_e}{n_e} \right) \mathbf{e}_i = \underbrace{\epsilon_{ijk} \frac{\partial_j \partial_k P_e}{n_e}}_{=0} \mathbf{e}_i - \epsilon_{ijk} \frac{(\partial_j n_e) (\partial_k P_e)}{n_e^2} \mathbf{e}_i = - \frac{\nabla n_e \times \nabla P_e}{n_e^2} \tag{4}\]

より

\[\frac{\partial \mathbf{B}}{\partial t} = \nabla \times (\mathbf{v} \times \mathbf{B}) - \frac{c \nabla n_e \times \nabla P_e}{e n_e^2} \tag{5}\]

のように整理されます。この第二項をビアマンバッテリー項と呼びます。この項は、磁場\(\mathbf{B}\)を含みません。このことから初期に磁場がゼロであっても、この項によって有限の磁場が生成されることがわかります。この項の物理的意味を直感的に理解してみましょう。下図は、電子一個に働く圧力による力と電場による力との釣り合いを示したものです。ただし、図の上側ほど数密度が大きくなっています。

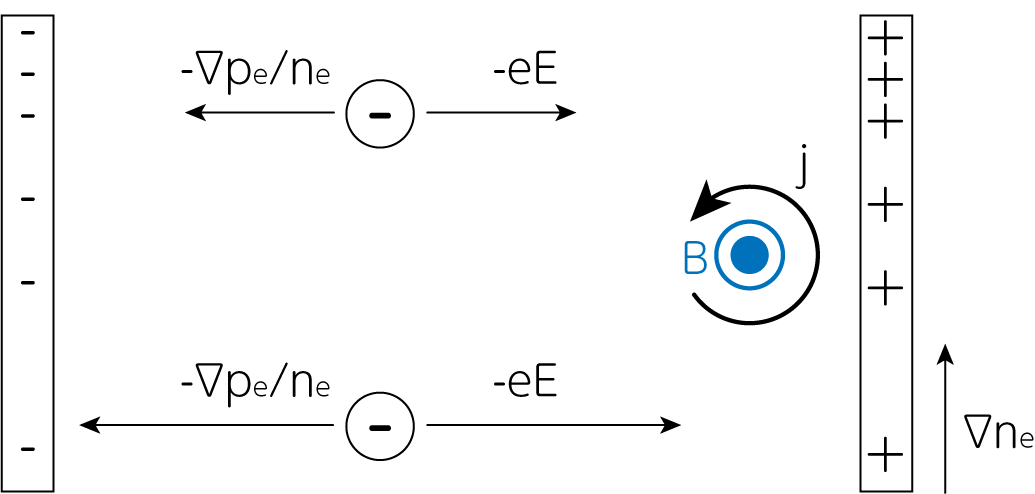
すると下側の方が上側に比べて圧力による力\(-\nabla P_e / n_e\)が大きくなるため、それと釣り合うように大きな電場が必要となることがわかります。電場の大きさの違いから\(\nabla \times \mathbf{E}\)が発生し、そこから磁場が紙面垂直方向に生成されるのです。
ビアマンバッテリーにより生成される磁場の大きさがどの程度か、そのオーダーを評価してみましょう。 (5)式より

\[\frac{B}{t_\mathrm{age}} \approx \frac{c}{e n_e^2} \frac{n_e}{\ell} \frac{P_e}{\ell} \sin \theta \ \Longrightarrow \ B \approx 5 \times 10^{-17} \left( \frac{t_\mathrm{age}}{2 \mathrm{Myr}} \right) \left( \frac{\sin \theta}{0.1}\right) \left( \frac{\ell}{1 \mathrm{pc}}\right)^{-2} \left( \frac{T_e}{10^4 \mathrm{K}}\right) \quad [\mathrm{G}] \tag{6}\]

のようになります。途中、\(\ell\)を系の典型的な長さスケール、\(\theta\)を\(\nabla n_e\)と\(\nabla P_e\)のなす角度としました。さらに\(P_e = n_e k_B T_e\)を用いました。かなり小さな値ではありますが、これにより有限の磁場が生成されることがわかりました。

最近の研究: 初代星周辺で起こる種磁場生成

このビアマンバッテリーは、宇宙初期の種磁場生成機構として注目されています。ここでは Doi & Susa 2011を例に見ていきましょう。この論文では、質量\(500M_\odot\)の初代星からの強烈な放射にさらされている銀河間物質の塊の時間発展を、放射による力とビアマンバッテリーを考慮した輻射磁気流体計算から調べました。

銀河間物質の塊(密度超過領域)に向かって、左から放射をぶつけます。このとき、密度超過領域が放射を遮ることで、その後方に放射の届かない影の領域を形成します。 4段目の右パネルに注目すると、\(t=2\mathrm{Myr}\)では黒線(電離波面)に沿って、\(10^{-18} \mathrm{G}\)程度の磁場が生成されていることがわかります。放射にさらされている部分は、電離によって電子数密度が大きくなります。電子数密度分布と電子圧力分布に差異が生まれ、そこから\(\nabla n_e \times \nabla p_e\)がゼロでない値となり、磁場が生成されています。
この論文では、さらに放射による力\(\mathbf{f}_\mathrm{rad}\)による磁場生成効果も考慮に入れています。 (1)式の右辺に\(\mathbf{f}_\mathrm{rad}\)を足し、さらに先程と同様に電子に働く力の釣り合いを考えると

\[\mathbf{E} = - \mathbf{v} \times \frac{\mathbf{B}}{c} - \frac{\nabla P_e}{e n_e} + \frac{\mathbf{f}_\mathrm{rad}}{en_e} \tag{7}\]

のようになります。これをファラデーの法則に代入すれば

\[\frac{\partial \mathbf{B}}{\partial t} = \nabla \times (\mathbf{v} \times \mathbf{B}) - \frac{c \nabla n_e \times \nabla P_e}{e n_e^2} - \frac{c}{e} \nabla \times \mathbf{f}_\mathrm{rad} \tag{8}\]

のように、放射による力の効果を考慮した式を得ることができます。ビアマンバッテリーによる磁場生成効果と放射による力の効果のどちらが重要かを調べたのが下図です。

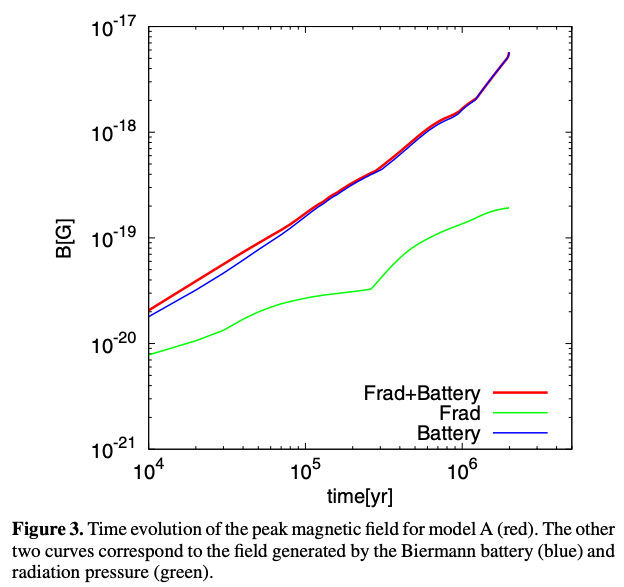
この図は磁場の最大値の時間発展を描画したもので、青線はビアマンバッテリーのみ、緑線は放射による力の効果のみ、そして赤線は両方を考慮した場合を表しています。この図から明らかなように、この論文で調査された現実的なパラメータにおいては、ビアマンバッテリー効果による磁場生成が優勢であることがわかります。

参考文献

[1] Biermann & Galea, 2003, “Origin of Cosmic Magnetic Fields”
[2] Ando et al., 2010, “Generation of Seed Magnetic Field around First Stars: Effects of Radiation Force”
[3] Doi & Susa, 2011, “Generation of a Seed Magnetic Filed around First Stars: the Biermann Battery Effect”
[4] Kulsrud, “Plama Physics for Astrophysics”
[5] 城本雄紀, “初代星周りの磁場生成”
[6] 市來淨與, “宇宙の磁場の起源 -密度揺らぎからの磁場生成とその観測的な応用について-“