チェレンコフ放射
問題設定
屈折率\(n_r\)の一様媒質中を、電荷\(q\)の荷電粒子が\(z\)軸に沿って等速直線運動で通り過ぎるときに発生する電磁放射を考えましょう。点電荷は\(z = -L/2\)から出発して\(t'=0\)で原点を通過します。そして\(z=L/2\)まで運動を行うとします。軸対称性より、観測者は\(yz\)平面内にいるとします。また観測者は、電子の運動を十分遠くから観察しているものとします。
観測者の方向を向いた単位ベクトルは
点電荷の位置ベクトルと速度ベクトルはそれぞれ
\[{\bf r}_0(t') = (0, 0, vt')\] \[\boldsymbol{\beta} = (0, 0, \beta) = (0, 0, v/c)\]となります。
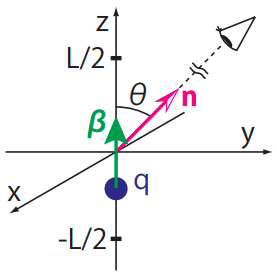
輻射場
加速度運動を伴わないために、輻射場である
\[{\bf E} = \frac{q}{c} \left[ \frac{\mathbf{n} \times ((\mathbf{n}-\boldsymbol{\beta})\times \dot{\boldsymbol{\beta}})}{\kappa^3 R} \right]\]は0になると思われるかもしれません。しかし屈折率\(n_r\)の媒質中では光の伝搬速度が\(c/n_r\)になることから
\[\kappa = 1- \mathbf{n} \cdot \boldsymbol{\beta} = 1-n_r \beta \cos \theta\]も0になりうることがわかります。よってこの輻射場によってエネルギーを無限遠方まで運ぶ電磁放射の存在が期待されます。ではその放射がどのような特徴を持っているのか、具体的な計算と物理的な解釈を行なっていきましょう。
フーリエスペクトル
観測時間が十分に長く、その長時間平均をとるとすると、輻射場のフーリエスペクトルは
\[\hat{\mathbf{E}}(\mathbf{r}, \omega)=-\frac{i \omega q}{2 \pi c / n_{r} R} e^{i \omega \frac{\mathbf{n} \cdot \mathbf{r}}{c / n_{r}}} \int_{T_{1}^{\prime}}^{T_{2}^{\prime}} \mathbf{n} \times(\mathbf{n} \times \boldsymbol{\beta}) e^{i \omega\left(t^{\prime}-\frac{\mathbf{r}_{0}\left(t^{\prime}\right) \cdot \mathbf{n}}{c / n_{r}}\right)} d t^{\prime} \tag{0}\]ここで注意しておきたいのは、\(\beta = v/(c/n_r)\)とはならないことです。\(\beta\)は荷電粒子の移動速度であり、屈折率が変わったからといって粒子の運動速度が半化することはありません。\(\kappa\)は荷電粒子が時空図上で運動することにより生じるドップラー効果からくるものなので、屈折率が1でない媒質中でその大きさが変わることは自然と言えるでしょう。
タム・フランクの式の導出
では計算を行なっていきましょう。
\[{\bf n} \times ({\bf n} \times \boldsymbol{\beta}) = ({\bf n} \cdot \boldsymbol{\beta}) {\bf n} - \boldsymbol{\beta} = \beta \cos \theta \left( \begin{array}{c} 0 \\ \sin \theta \\ \cos \theta \end{array} \right) - \beta \left( \begin{array}{c} 0 \\ 0 \\ 1 \end{array} \right) = \beta \left( \begin{array}{c} 0 \\ \sin \theta \cos \theta \\ -\sin^2 \theta \end{array} \right) \tag{1}\] \[t' - \frac{\mathbf{r}_0 \cdot \mathbf{n}}{c/n_r} = t' - \frac{n_r}{c} vt' \cos \theta = (1-n_r \beta \cos \theta) t'\]また問題設定より\(T'_1 = -T'_2 = -L/(2v)\)です。粒子が\(z=-L/2\)から\(z=L/2\)まで駆け抜けるのに要する時間を\(T'\equiv L/v\)と定義しておきます。
(1)の\(x\)成分より
(0), (1)より、\(y\)成分は
\[\begin{aligned} \hat{E}_{y}(\mathbf{r}, \omega) &=-\frac{i \omega q n_{r}}{2 \pi c R} \beta \sin \theta \cos \theta e^{i \omega \frac{\mathrm{n} \cdot \mathrm{r}}{c / n_{r}}} \int_{-T^{\prime} / 2}^{T^{\prime} / 2} e^{i \omega\left(1-n_{r} \beta \cos \theta\right) t^{\prime}} d t^{\prime} \\ &=-\frac{i \omega q n_{r}}{2 \pi c R} \beta \sin \theta \cos \theta e^{i \omega \frac{n \cdot r}{c / n_{r}}} \frac{e^{i \omega\left(1-n_{r} \beta \cos \theta\right) T^{\prime} / 2}-e^{-i \omega\left(1-n_{r} \beta \cos \theta\right) T^{\prime} / 2}}{i \omega\left(1-n_{r} \beta \cos \theta\right)} \\ &=-\frac{i \omega q n_{r}}{2 \pi c R} \beta \sin \theta \cos \theta e^{i \omega \frac{n \cdot r}{c / n_{r}}} \frac{2 i \sin \left\{\omega\left(1-n_{r} \beta \cos \theta\right) \frac{T^{\prime}}{2}\right\}}{i \omega\left(1-n_{r} \beta \cos \theta\right)} \\ &=-\frac{i \omega q n_{r}}{\pi c R} \beta \sin \theta \cos \theta e^{i \omega \frac{\mathrm{n} \cdot r}{n n}} \frac{T^{\prime}}{2} \operatorname{sinc}\left\{\omega\left(1-n_{r} \beta \cos \theta\right) \frac{T^{\prime}}{2}\right\} \end{aligned}\]\(\hat{E}_y\)と\(\hat{E}_z\)の違いは\(\sin \theta \cos \theta\)と\(-\sin^2 \theta\)の違いのみなので
\[\hat{E}_z = \frac{i \omega q n_{r}}{\pi c R} \beta \sin^2 \theta e^{i \omega \frac{\mathrm{n} \cdot r}{n n}} \frac{T^{\prime}}{2} \operatorname{sinc}\left\{\omega\left(1-n_{r} \beta \cos \theta\right) \frac{T^{\prime}}{2}\right\}\]ここで上式のsinc関数の中について考えてみましょう。\(T'\)の定義と合わせて
\[\omega (1-n_r \beta \cos \theta) \frac{T'}{2} = \frac{\omega}{c} c \frac{L}{2n} (1- n_r \beta \cos \theta) = \frac{\omega}{c} L \frac{1}{2\beta} (1- n_r \beta \cos \theta)\]\(\omega /c\)は真空中での電磁波の波数です。よって粒子の走る距離\(L\)が十分長く\(\omega L /c \gg 1\)とするとsinc関数は\(1- n_r \beta \cos \theta \simeq 0\)でピークを持つような\(\delta\)関数的な振る舞いをすることがわかります。このことから、この電磁波の特徴を考えてみましょう。
\[1-n_r \beta \cos \theta = 0 \ \Longrightarrow \ \frac{c}{n_r} T' = v T' \cos \theta \tag{2}\]左辺は\(T'\)間に電磁波が到達する距離、右辺の\(vT'\)は荷電粒子の移動距離です。よってこの電磁波は半頂角\(\pi/2 - \theta\)の円錐状に強い強度を持って広がっていることがわかります(下図参照)。
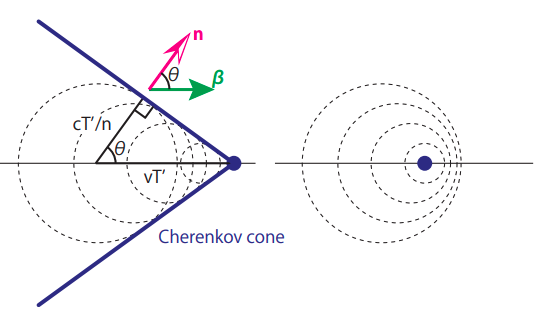
この図では異なる時刻に放出される球面波を4つ描いています。粒子の速度が速い左図では4つの球面波からさらに共通波面を見いだすことができます。ホイヘンスの原理から、この共通波面がチェレンコフ放射として観測されます。一方、右図では粒子の速度が遅いために、4つの球面波から共通波面をつくり上げることはできません。すなわち荷電粒子の運動速度が遅く、(2)式が満たされない場合、チェレンコフ放射は観測されないことになります。
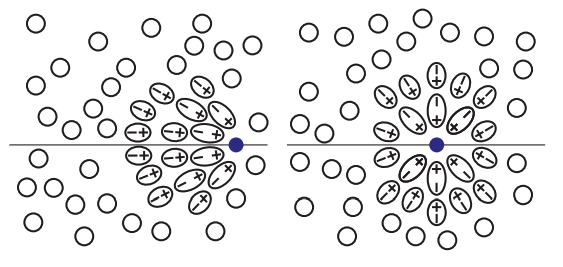
光速度に近い速度で運動する荷電粒子が作る電磁場は相対論的ビーミングにより、上図で点線で描かれているような円形ではありません。実際には、光速度に近い速度で運動する点電荷によって置いてけぼりとなった電磁場が、下図の左のように周囲の原子・分子に分極を起こします。これらの分極状態が元の中性の状態に戻るときに放射を出します。これらの重ね合わせが電磁的な衝撃波となり、チェレンコフ放射として我々に観測されるのです。一方で、荷電粒子の速度が媒質中の光速度に比べて遅い場合は、周囲の物質の分極は等方的となります右図。よってこれらの分極が元の状態に戻るときに放出される放射は打ち消しあい、我々には観測されません。
単位時間、単位周波数、単位立体角あたりの放射強度を求めましょう。
\[\begin{aligned} &\frac{d W}{d \omega d \Omega d t^{\prime}}=\frac{c / n_{r} R^{2}}{T^{\prime}}\left(\left|\hat{E}_{x}\right|^{2}+\left|\hat{E}_{y}\right|^{2}+\left|\hat{E}_{z}\right|^{2}\right)=\frac{q^{2} n_{r}}{\pi^{2} c} \omega^{2} \beta^{2} \sin ^{2} \theta \underbrace{\left(\cos ^{2} \theta+\sin ^{2} \theta\right)}_{=1} \frac{T^{\prime}}{4} \operatorname{sinc}^{2}\left\{\omega\left(1-n_{r} \beta \cos \theta\right) \frac{T^{\prime}}{2}\right\} \\ &\underbrace{=}_{T^{\prime}=L / v} \frac{q^{2}}{2 \pi^{2} c} \omega \beta \sin ^{2} \theta \frac{\omega L n_{r} \beta}{2 c v / c} \operatorname{sinc}^{2}\left\{\frac{\omega L n_{r} \beta}{2 c v / c}\left(\frac{1}{n_{r} \beta}-\cos \theta\right)\right\} \\ &\underbrace{=}_{\operatorname{sinc}^{2} \text { is even }} \frac{q^{2}}{2 \pi^{2} c} \omega \beta \sin ^{2} \theta \frac{\omega L n_{r}}{2 c} \operatorname{sinc}^{2}\left\{\frac{\omega L n_{r}}{2 c}\left(\cos \theta-\frac{1}{n_{r} \beta}\right)\right\} \end{aligned}\]ここで\(a {\rm sinc}^2 ab\)を\(b\)について区間\([-\infty, \infty]\)で積分した値から
\[\int_{-\infty}^\infty a {\rm sinc}^2 (ab) db \underbrace{=}_{\alpha = ab} \int_{-\infty}^\infty {\rm sinc}^2 \alpha d\alpha = \pi \ \Longrightarrow \ \lim_{a\rightarrow \infty} a {\rm sinc}^2 ab = \pi \delta (b)\]と考えることができます。今、\(\omega L n_r / (2c) \rightarrow \infty\)と考えることができるので
\[\frac{dW}{d\omega d\Omega dt'} = \frac{q^2}{2\pi c} \omega \beta \sin^2 \theta \delta (\cos \theta - \frac{1}{n_r \beta})\]これを全立体角で積分を行います。
\[\frac{dW}{d\omega dt'} = \frac{q^2}{2\pi c} \omega \beta \int_0^{2\pi} d\varphi \int_0^\pi \sin^2\theta \delta (\frac{1}{n_r \beta} - \cos \theta) \sin \theta \underbrace{=}_{\mu = \cos^2 \theta} \frac{q^2}{c} \omega \beta \int_{-1}^1 (1-\mu^2) \delta (\mu - \frac{1}{n_r \beta}) d \mu\]積分値が0でない値となる、すなわちチェレンコフ放射が存在するための条件は
\[1/|n_r \beta| < 1 \ \Longrightarrow \ n_c v / c > 1 \ \Longrightarrow \ v > c/n_r\]となり、図を用いた議論などと一致することがわかります。
\[\therefore \ \frac{dW}{d\omega dt'} = \frac{q^2}{c} \omega \beta (1-\frac{1}{n_r^2 \beta^2})\]この両辺を\(t'\)で積分すると
\[\frac{dW}{d\omega} =\frac{q^2}{c} \omega \beta (1-\frac{1}{n_r^2 \beta^2}) \int_{-T'/2}^{T'/2} dt' \underbrace{=}_{T' = L/v} \frac{q^2}{c^2} \omega (1-\frac{1}{n_r^2 \beta^2}) L\]よって、単位周波数、単位距離あたりに荷電粒子が電磁波として放出する放射のエネルギーは
\[\frac{dW}{d\omega dz} = \frac{q^2 \omega}{c^2} \left( 1-\frac{1}{n_r^2 \beta^2}\right) \tag{3}\]この式はソビエト連邦(現ロシア)の物理学者Ilya FrankとIgor Tammによって1937年に理論的に示されました。これはTamm-Frank formula(タム・フランクの式)と呼ばれています。チェレンコフ放射それ自体は同じくソビエトの物理学者Pavel Cherenkovにより 1934 年に発見されていたため、この両者はその3年後に理論体系を築き上げたことになります。「チェレンコフ効果の発見とその解釈」の事由により、3者は1958年にノーベル物理学賞を受賞しました。
この研究を礎として、近年ではチェレンコフ放射を利用してニュートリノ観測を行うことが話題となっています(2002年ノーベル物理学賞の小柴昌俊、2015年ノーベル物理学賞の梶田隆章とArthur McDonald)。ニュートリノ自身は電荷を持ちませんが、ニュートリノが媒質中で電子をはじき出すあるいはニュートリノが原子核と反応しミューオンや電子を放出することによって、電荷を持った粒子が媒質中を駆け抜けます。これによりチェレンコフ放射が観測されます。
光子数に変換
\(E=\hbar \omega\)の光子数を\(N\)とすると
\[W = NE = \hbar \omega N \ \Longrightarrow \ dW = \hbar \omega dN, \ dE = \hbar d\omega\]より、単位エネルギー単位距離あたりに荷電粒子が放出する光子数は
\[\frac{dN}{dE dz} = \frac{q^2}{\hbar^2 c^2} \left( 1-\frac{1}{n_r^2 \beta^2}\right) = \frac{\alpha Z^2}{\hbar c} \left( 1-\frac{1}{n_r^2 \beta^2}\right) \tag{4}\]となります。途中\(q = Ze\)と微細構造定数\(\alpha = e^2 /\hbar c \sim 1/ 137\)を用いました。