Table of contents
2.6.1 Eddington Approximation
以前に大気の十分深いところでは\(J_\nu \simeq 3 K_\nu\)となることを(2.33), (2.52)式で導出しました。Eddington 近似では
\[J = 3K \tag{2.62}\]の関係がどこでも成り立っていることを仮定します。この関係を(2.61)式に用いると
\[J_E (\tau) = \frac{3}{4\pi} F \tau + C' \tag{2.63}\]が得られます。(2.58)式の関係\(S = J\)より
\[S(\tau) = J_E (\tau) = \frac{3}{4\pi} F \tau + C'\]となり、Source function \(S\)がOptical depth \(\tau\)の関数で与えられることになります。よってRadiative transferの式(2.56)の解は、形式解(2.16)で与えられます。Flux \(F\)はExponentical integral \(E_2\)を用いて(2.40)式で与えられます。よって(2.40)式に\(S(\tau)\)を代入すると
\[F = F(0) = 2\pi \int_0^\infty J(t) E_2 (t) dt = 2\pi \int_0^\infty \left( \frac{3}{4\pi} Ft + C' \right) E_2 (t) dt\]最初の等式は\(F = {\rm Const}\)であることを用いました。Exponentical integralについて成り立つ関係式\(E_n (x) = -E'_{n+1}(x)\)の関係を用いて
\[\begin{aligned} F &= -2\pi \int_0^\infty \left( \frac{3}{4\pi} Ft + C' \right) \frac{dE_3}{dt} dt = -2\pi \left\{ \left[ E_3(t) \left( \frac{3F}{4\pi} t + C' \right)\right]_0^\infty - \int_0^\infty \frac{3}{4\pi} F E_3 (t) \right\} \\ &= -2\pi \left( -E_3 (0) C' + \frac{3}{4\pi} F \left[ E_4 (t) \right]_0^\infty \right) = 2\pi C' E_3 (0) + \frac{3F}{2} E_4(0) \end{aligned}\]ここで\(E_n (0) = 1/ (n-1)\)を使うと
\[F = \pi C' + \frac{1}{2} F \ \Longrightarrow \ C' = \frac{F}{2\pi} \tag{2.64}\]よって、(2.63)式は
\[J_E (\tau) = \frac{3F}{4\pi} \left( \tau + \frac{2}{3} \right) \tag{2.65}\]となります。LTEにおいて
\[J = \int_0^\infty J_\nu d\nu = \int_0^\infty B_\nu d\nu = B = \frac{\sigma}{\pi} T^4\]さらに\(F = F(0) = \sigma T_{\rm{eff}}^4\)より
\[T^4 (\tau) = \frac{3}{4} T_{\rm{eff}}^4 \left( \tau + \frac{2}{3} \right) \tag{2.66}\]のように温度とOptical depthの関係に変換されます。この式から、\(\tau=0\)での温度\(T_0\)とEffective temperature \(T_{\rm{eff}}\)との比が\(T_0/T_{\rm{eff}} = (1/2)^{1/4} \sim 0.841\)であることを示しています。この値は、厳密な値である0.8114から遠くない値であることが知られています。またこの式は\(\tau = 2/3\)で\(T = T_{\rm{eff}}\)になっており、この深さが光球(連続光が放出される層)であることを示しています。この層から出た光子が表面\((\tau=0)\)まで出てくる確率は、\(e^{-2/3}\sim 0.5\)で光球の概念と合致しています。
\(S = J\)より(2.65)式を(2.19)式に用いて、\(\tau = 0\)で外側に向かう\((0\leq \mu \leq 1)\) Intensityを求めましょう。
\[I_E^+(0, \mu) = \frac{3}{4\pi} F \int_0^\infty \left( t+ \frac{2}{3} \right) e^{-t/\mu} \frac{dt}{\mu} = \frac{3F}{4\pi} \left( \mu + \frac{2}{3} \right) \tag{2.67}\]これはSource functionがOptical depthの線型関数であれば、Emergent intensityが\(\tau = \mu\)の場所のSource functionになる、というEddington-Barbier relationの特別な形になっています。この式から得られるLimb-darkeningは
\[\frac{I_E^+ (0, \mu)}{I_E^+ (0, 1)} = \frac{3}{5} \left( \mu + \frac{2}{3} \right) \tag{2.68}\]のようになります。太陽ディスクの端\((\mu = 0)\)のIntensityが中央の40%であることを示しています。これは可視光での観測とよく合っています。
2.6.2 一般の場合
特別な近似を使わない場合はRadiative transferの式(2.59)は解析的に解くことができません。この式の難しさは
\[J = \frac{1}{2} \int_{-1}^1 I(\tau, \mu) d\mu \tag{2.69}\]より、積分-微分方程式になっていることに由来します。数値的に解く方法として、Variable Eddington-factorの方法があります。この方法では、Eddington-factor
\[f(\tau) = \frac{K(\tau)}{J(\tau)} \tag{2.70}\]を導入します。Eddington approximationでは\(f_E = 1/3\)ですが、一般には場所によって変化する量です。最初に\(f(\tau)\)の値を仮定すると、(2.61)式を用いて、(2.59)式を数値的に解いて\(I(\tau, \mu)\)を種々の\(\mu\)の値に対して得ることができます。これを(2.69)式に使うと\(J(\tau)\)が求まり
\[K(\tau) = \frac{1}{2} \int_{-1}^1 \mu^2 I(\tau, \mu) d\mu \tag{2.71}\]から\(K(\tau)\)が求まります。これらから再び\(f(\tau)\)を決定することができます。この値は一般に最初に仮定した値とは異なっているので、上の計算を\(f(\tau)\)の仮定した値と得られた値とが同じになるまで繰り返すと\(I, J, K\)の厳密な解が得られます。
厳密解では、(2.65)式の代わりに
のように表されます。\(q(\tau)\)はHopf functionとして知られます。Eddington近似では\(2/3\)となります。\(f(\tau), q(\tau)\)の関係を示しましょう。(2.61), (2.72)式より
\[\frac{1}{3} J(\tau) - K(\tau) = \frac{F}{4\pi} \left\{ q(\tau) - \frac{4\pi}{F} C\right\} \tag{2.73}\]の関係が得られます。\(\tau \rightarrow \infty\)では輻射は等方的になるので、\(K \rightarrow J/3\)という境界条件が得られます。よって
\[C = \frac{F}{4\pi} q(\infty)\]よって
\[K(\tau) = \frac{F}{4\pi} \left\{ \tau + q(\infty) \right\} \tag{2.74}\]のように表されます。したがってEddington factorは
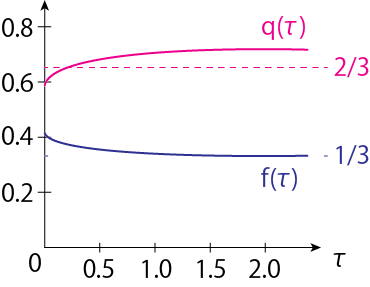
\[f(\tau) = \frac{K}{J} = \frac{\tau + q(\infty)}{3\{ \tau + q(\tau) \}} \tag{2.75}\]のようになります。下図は\(q(\tau), f(\tau)\)を表しています。\(\tau\)がある程度大きくなると\(f\)が1/3に近くなっていることが見て取れます。
またLTEを仮定すると\(J = B = \frac{\sigma}{\pi} T^4\)より、温度分布が
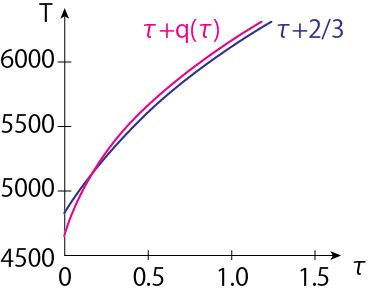
\[T^4 = \frac{3}{4} T_{\rm{eff}}^4 \{\tau + q(\tau)\} \tag{2.76}\]のように表されます。下図はEddington近似の場合と厳密解の場合で温度分布を比較したものです。